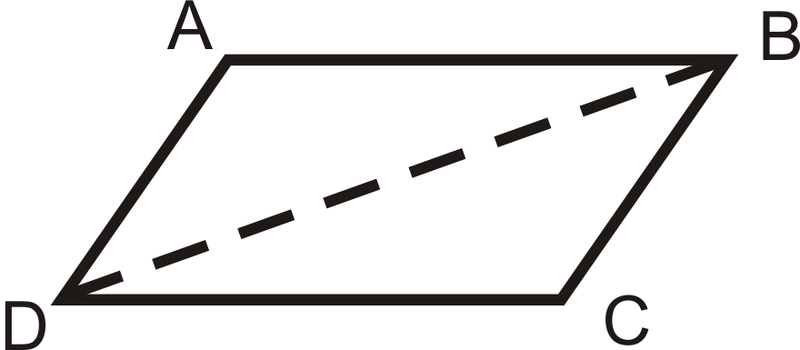
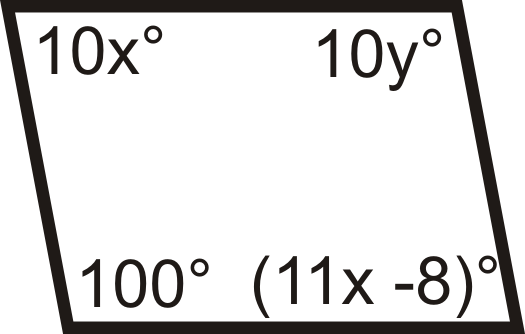6.4 平行形四边形

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节平行方形的四边形

  折叠 展开

  平行方形的四边形

  播放段落

  Quadrilaterals that are Parallelograms
  ::平行方形的四边形

  播放段落

  Recall that a is a quadrilateral with two pairs of parallel sides. Even if a quadrilateral is not marked with having two pairs of sides, it still might be a parallelogram. The following is a list of theorems that will help you decide if a quadrilateral is a parallelogram or not.
  ::回顾 a 是两对平行面的四边形。 即使一个四边形没有标记为两对面, 也可能是一个平行图。 下面列出一系列的理论, 帮助您决定四边形是否是平行图。

  播放段落

  1.   Opposite Sides Theorem Converse: If both pairs of opposite sides of a quadrilateral are congruent , then the figure is a parallelogram.
  ::1. 对面侧理论对立:如果四边形对面对面对面对面对面的对面对齐,则数字为平行图。

  播放段落

  If then
  ::如果当时

  播放段落

  2.   Opposite Angles Theorem Converse: If both pairs of opposite angles of a quadrilateral are congruent, then the figure is a parallelogram.
  ::2. 对角角理论对立:如果四边形对面角度对面对面的对面对面对齐,则数字为平行图。

  播放段落

  If then
  ::如果当时

  播放段落

  3.   Parallelogram Diagonals Theorem Converse: If the diagonals of a quadrilateral bisect each other, then the figure is a parallelogram.
  ::3. 平行对角线理论对立面:如果四边形对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线线对角线对角线对角线对角线线对角线对角线对角线对角线线对角线线对角线线对角线对角线对角线线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线的对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线线对角线对角线对角线的对角线对角线对角线对角线对角线对角线对角线对角线的对角线对角线对角线对角线对角线形对角线对角线形对角线形对角线对角线对角线形对角线形对角线形对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线对角线的对角线对角线对角线对角线对角线形对角线对角线的对角线对角线对角线形对角线的对角线对角线对角线对角线形对角线形对角线形对角线对角线对角线形对角形对角形对角线对角线对角线对角形对角形对角形对角形对角形对角形对角形对

  播放段落

  If then
  ::如果当时

  播放段落

  4.   Parallel Congruent Sides Theorem: If a quadrilateral has one set of parallel lines that are also congruent, then it is a parallelogram.
  ::4. 平行共性侧面理论:如果一个四边形有一套平行线条,也具有相同的平行线条,那么它就是一个平行图。

  播放段落

  If then
  ::如果当时

  播放段落

  You can use any of the above theorems to help show that a quadrilateral is a parallelogram. If you are working in the $\begin{align*}x-y\end{align*}$ plane , you might need to know the formulas shown below to help you use the theorems.
  ::您可以使用上述任何一种理论来帮助显示四边形是一个平行图。如果您在 X - y 平面上工作,可能需要知道下面显示的公式来帮助您使用这些理论。

  播放段落
  • The Slope Formula, $\begin{align*}\frac{y_2 - y_1}{x_2 - x_1}\end{align*}$ . (Remember that if slopes are the same then lines are parallel).
    ::斜坡公式, y2 - y1x2 - x1 (记住, 如果斜坡相同, 那么线则平行) 。
  播放段落
  • The Distance Formula, $\begin{align*}\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\end{align*}$ . (This will help you to show that two sides are congruent).
    ::距离公式, (x2- x1) 2+(y2-y1) 2. (这将帮助您显示两面是相同的 ) 。
  播放段落
  • The Midpoint Formula, $\begin{align*}\left ( \frac{x_1 + x_2 }{2} , \frac{y_1 + y_2}{2} \right )\end{align*}$ . (If the midpoints of the diagonals are the same then the diagonals bisect each other).
    ::中点公式, (x1+x22,y1+y22) 。 (如果对角线的中点相同, 则对角线相互交叉) 。

  播放段落

  What if you were given four pairs of coordinates that form a quadrilateral? How could you determine if that quadrilateral is a parallelogram?
  ::如果给你们四对坐标组成四边形呢?你怎么确定四边形是平行图呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Prove the Parallel Congruent Sides Theorem.
  ::证明平行的共性侧面理论

  

  播放段落

  Given : $\begin{align*}\overline{AB} \| \overline{DC}\end{align*}$ , and $\begin{align*}\overline{AB} \cong \overline{DC}\end{align*}$
  ::以:'AB'D,'A'D'D,'A'D'D

  播放段落

  Prove : $\begin{align*}ABCD\end{align*}$ is a parallelogram
  ::证明: ABCD 是平行图

  Statement	Reason
  1. $\begin{align*}\overline{AB} \| \overline{DC}\end{align*}$ , and $\begin{align*}\overline{AB} \cong \overline{DC}\end{align*}$	1. Given
  2. $\begin{align*}\angle ABD \cong \angle BDC\end{align*}$	2.
  3. $\begin{align*}\overline{DB} \cong \overline{DB}\end{align*}$	3. Reflexive PoC
  4. $\begin{align*}\triangle ABD \cong \triangle CDB\end{align*}$	4.
  5. $\begin{align*}\overline{AD} \cong \overline{BC}\end{align*}$	5.
  6. $\begin{align*}ABCD\end{align*}$ is a parallelogram	6. Opposite Sides Converse

  播放段落

  Example 2
  ::例2

  播放段落

  What value of $\begin{align*}x\end{align*}$ would make $\begin{align*}ABCD\end{align*}$ a parallelogram?
  ::x 的值如何使 ABCD 变成平行图 ?

  

  播放段落

  $\begin{align*}\overline{AB} \| \overline{DC}\end{align*}$ . By the Parallel Congruent Sides Theorem, $\begin{align*}ABCD\end{align*}$ would be a parallelogram if $\begin{align*}AB = DC\end{align*}$ .
  ::根据平行的共性侧面理论,ABCD是平行的,如果AB=DC的话。

  播放段落

  $$\begin{align*}5x - 8 & = 2x + 13\\ 3x & = 21\\ x & = 7\end{align*}$$
  ::5x-8=2x+133x=21x=7

  播放段落

  Example 3
  ::例3

  播放段落

  Prove the Opposite Sides Theorem Converse.
  ::证明对面侧理论对立。

  

  播放段落

  Given : $\begin{align*}\overline{AB} \cong \overline{DC}, \overline{AD} \cong \overline{BC}\end{align*}$
  ::给:'A'A'D'D,'A'A'D'A'C'A'A'B&B

  播放段落

  Prove : $\begin{align*}ABCD\end{align*}$ is a parallelogram
  ::证明: ABCD 是平行图

  Statement	Reason
  1. $\begin{align*}\overline{AB} \cong \overline{DC}, \overline{AD} \cong \overline{BC}\end{align*}$	1.Given
  2. $\begin{align*}\overline{DB} \cong \overline{DB}\end{align*}$	2. Reflexive PoC
  3. $\begin{align*}\triangle ABD \cong \triangle CDB\end{align*}$	3.
  4. $\begin{align*}\angle ABD \cong \angle BDC, \angle ADB \cong \angle DBC\end{align*}$	4. CPCTC
  5. $\begin{align*}\overline{AB} \| \overline{DC}, \overline{AD} \| \overline{BC}\end{align*}$	5. Alternate Interior Angles Converse
  6. $\begin{align*}ABCD\end{align*}$ is a parallelogram	6. Definition of a parallelogram

  播放段落

  Example 4
  ::例4

  播放段落

  Is quadrilateral $\begin{align*}EFGH\end{align*}$ a parallelogram? How do you know?
  ::EFGH四边形是平行图吗?

  

  播放段落

  By the Opposite Angles Theorem Converse, $\begin{align*}EFGH\end{align*}$ is a parallelogram.
  ::EFGH是一个平行图。

  播放段落

  $\begin{align*}EFGH\end{align*}$ is not a parallelogram because the diagonals do not bisect each other.
  ::EFGH并不是一个平行的图形,因为对角体不会相互分离。

  播放段落

  Example 5
  ::例5

  播放段落

  Is the quadrilateral $\begin{align*}ABCD\end{align*}$ a parallelogram?
  ::四边 ABCD 是平行图吗?

  

  播放段落

  Let’s use the Parallel Congruent Sides Theorem to see if $\begin{align*}ABCD\end{align*}$ is a parallelogram. First, find the length of $\begin{align*}AB\end{align*}$ and $\begin{align*}CD\end{align*}$ using the distance formula.
  ::让我们使用平行的 Congruent 侧面理论来查看 ABCD 是否是一个平行图。 首先,使用距离公式来查找 AB 和 CD 的长度 。

  播放段落

  $$\begin{align*}AB & = \sqrt{(-1-3)^2 + (5 - 3)^2} && CD = \sqrt{(2 - 6)^2 + (-2 + 4)^2}\\ & = \sqrt{(-4)^2 + 2^2} && = \sqrt{(-4)^2 + 2^2}\\ & = \sqrt{16 + 4} && = \sqrt{16 + 4}\\ & = \sqrt{20} &&= \sqrt{20}\end{align*}$$
  ::AB(-1-3)2+(5-3)2+(5-6)2CD(2-6)2+(-2+4)2+(-4)2+(4)2+22__(4)2+22__(4)2+22}16+4}16+4}16+416+4}20

  播放段落

  Next find the slopes to check if the lines are parallel.
  ::下一步找到斜坡以检查线条是否平行 。

  播放段落

  $\begin{align*}\text{Slope}\ AB = \frac{5 - 3}{-1-3} = \frac{2}{-4} = -\frac{1}{2} \qquad \text{Slope}\ CD = \frac{-2 +4}{2-6} = \frac{2}{-4} = -\frac{1}{2}\end{align*}$
  ::斜坡 AB= 5-3 - 1 - 3= 2 - 4 12 斜坡 CD=2+42-6=2 - 412

  播放段落

  $\begin{align*}AB = CD\end{align*}$ and the slopes are the same (implying that the lines are parallel), so $\begin{align*}ABCD\end{align*}$ is a parallelogram.
  ::AB=CD,斜坡相同(暗示线线是平行的),所以ABCD是平行图。

  播放段落

  Review
  ::回顾

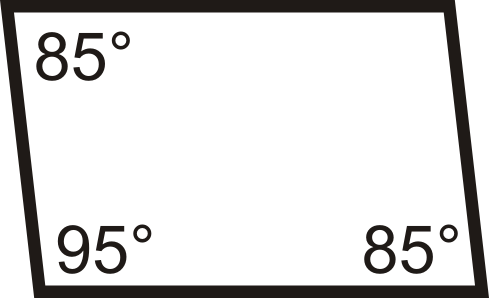
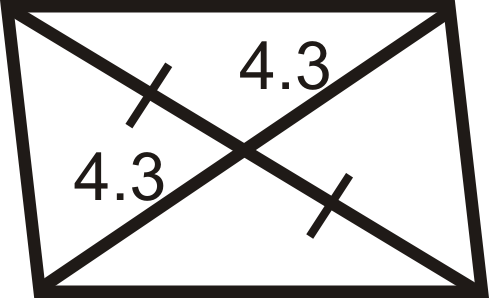
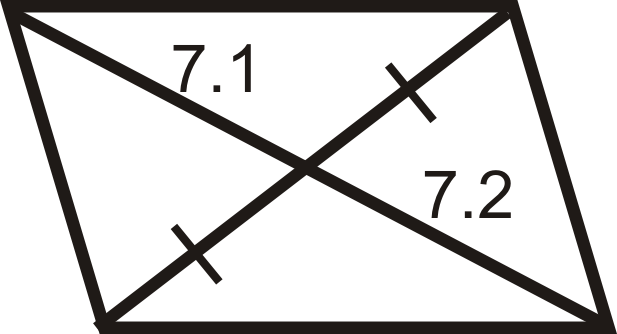
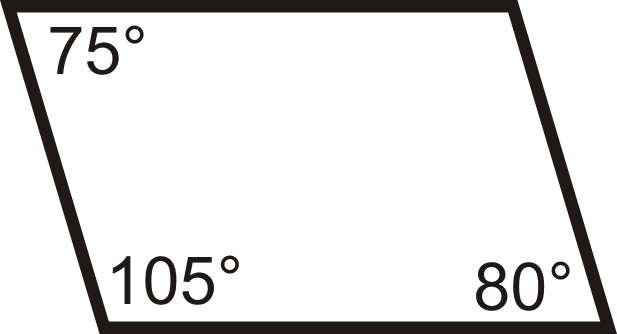
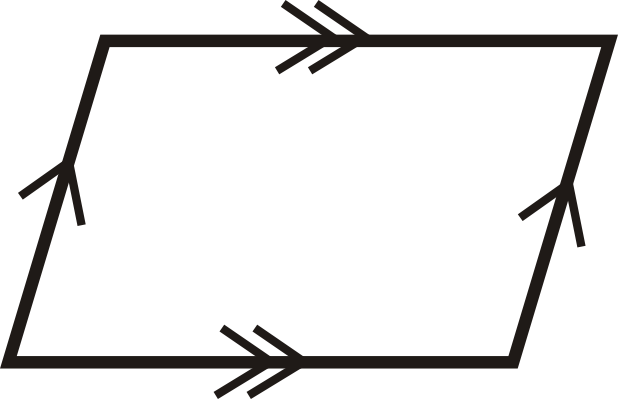
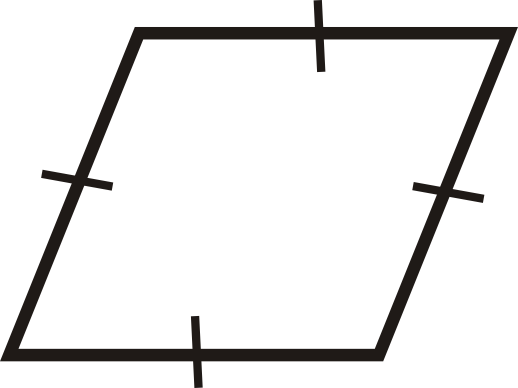
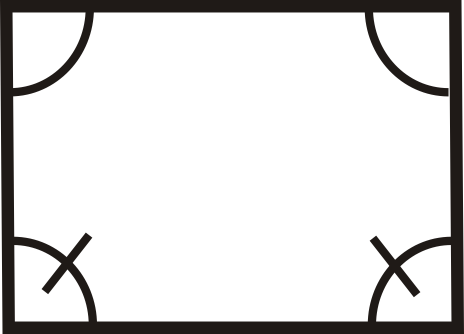
  播放段落

  For questions 1-12, determine if the quadrilaterals are parallelograms.
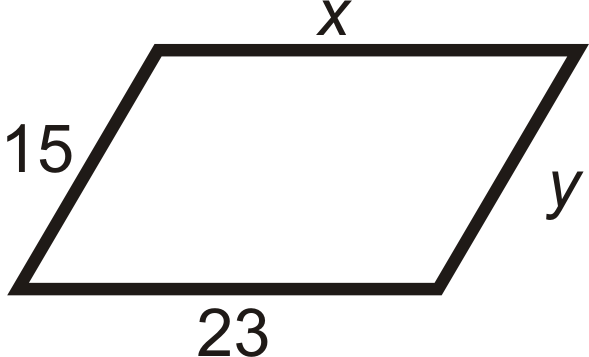
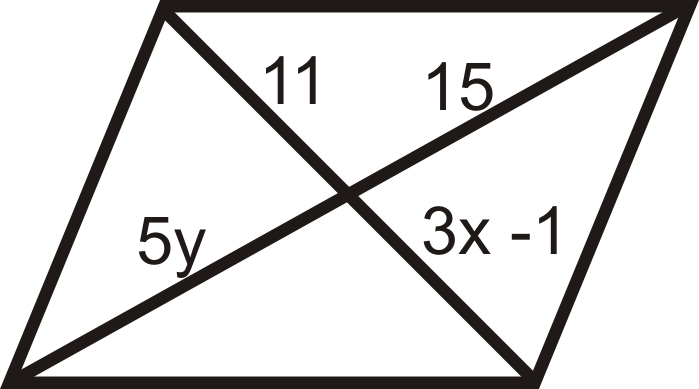
  ::对于问题1-12,确定四边形是否为平行图。

  1. 
  2. 
  3. 
  4. 
  5. 
  6. 
  7. 
  8. 
  9. 
  10. 
  11. 
  12. 

  播放段落

  For questions 13-18, determine the value of $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ that would make the quadrilateral a parallelogram.
  ::对于问题13-18,确定x和y的值,使四边形成为平行图。

  13. 
  14. 
  15. 
  16. 
  17. 
  18. 

  播放段落

  For questions 19-22, determine if $\begin{align*}ABCD\end{align*}$ is a parallelogram.
  ::对于问题19-22,确定ABCD是否是一个平行图。

  播放段落
  19. $\begin{align*}A(8, -1), B(6, 5), C(-7, 2), D(-5, -4)\end{align*}$
      ::A(8)-1,B(6),B(6),B(5),C(-7),C(-7),D(-5)-4
  播放段落
  20. $\begin{align*}A(-5, 8), B(-2, 9), C(3, 4), D(0, 3)\end{align*}$
      ::A(-5,8),B(-2,9),C(3,4,4),D(0,3)
  播放段落
  21. $\begin{align*}A(-2, 6), B(4, -4), C(13, -7), D(4, -10)\end{align*}$
      ::A(2,2,6),B(4,4,4),C(13,-7),D(4,10)
  播放段落
  22. $\begin{align*}A(-9, -1), B(-7, 5), C(3, 8), D(1, 2)\end{align*}$
      ::A(-9,-1),B(-7,5),C(3,3,8,D(1,2)

  播放段落

  Fill in the blanks in the proofs below.
  ::填充以下证据中的空白。

  播放段落
  23. Opposite Angles Theorem Converse
      ::反对角角定理

  

  播放段落

  Given : $\begin{align*}\angle A \cong \angle C, \angle D \cong \angle B\end{align*}$
  ::来源: @AC, @DB

  播放段落

  Prove : $\begin{align*}ABCD\end{align*}$ is a parallelogram
  ::证明: ABCD 是平行图

  Statement	Reason
  1.	1.
  2. $\begin{align*}m \angle A = m \angle C, m \angle D = m \angle B\end{align*}$	2.
  3.	3. Definition of a quadrilateral
  4. $\begin{align*}m \angle A + m \angle A + m \angle B + m \angle B = 360^\circ\end{align*}$	4.
  5.	5. Combine Like Terms
  6.	6. Division PoE
  7. $\begin{align*}\angle A\end{align*}$ and $\begin{align*}\angle B\end{align*}$ are supplementary $\begin{align*}\angle A\end{align*}$ and $\begin{align*}\angle D\end{align*}$ are supplementary	7.
  8.	8. Consecutive Interior Angles Converse
  9. $\begin{align*}ABCD\end{align*}$ is a parallelogram	9.

  播放段落
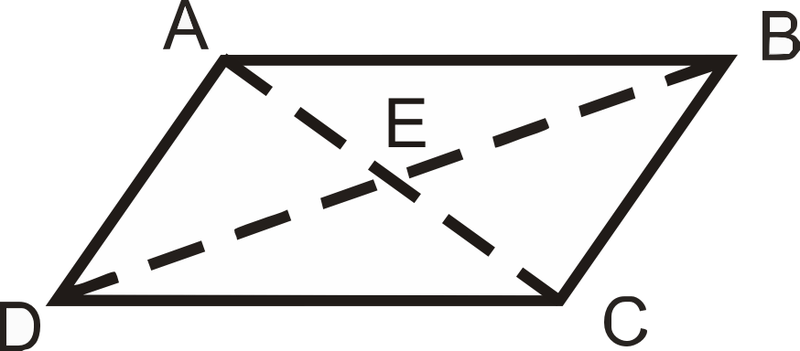
  24. Parallelogram Diagonals Theorem Converse
      ::平行对角对角定理

  

  播放段落

  Given : $\begin{align*}\overline{AE} \cong \overline{EC}, \overline{DE} \cong \overline{EB}\end{align*}$
  ::给:AE'EEC,E'E'E

  播放段落

  Prove : $\begin{align*}ABCD\end{align*}$ is a parallelogram
  ::证明: ABCD 是平行图

  Statement	Reason
  1.	1.
  2.	2. Vertical Angles Theorem
  3. $$\begin{align*}\triangle AED & \cong \triangle CEB\\ \triangle AEB & \cong \triangle CED\end{align*}$$	3.
  4.	4.
  5. $\begin{align*}ABCD\end{align*}$ is a parallelogram	5.

  播放段落
  25. Given : $\begin{align*}\angle ADB \cong \angle CBD, \overline{AD} \cong \overline{BC}\end{align*}$ Prove : $\begin{align*}ABCD\end{align*}$ is a parallelogram
      ::ABCD是一张平行图。

  

  Statement	Reason
  1.	1.
  2. $\begin{align*}\overline{AD} \| \overline{BC}\end{align*}$	2.
  3. $\begin{align*}ABCD\end{align*}$ is a parallelogram	3.

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。