Course: 1.22 三角函数的范围、范围和标志

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

三角函数的域域、范围及符号

You are doodling in art class one day when you draw a circle. Then you draw a few lines extending outward from the center to the edge of the circle. You draw a triangle with the "x" axis, and realize that you're thinking about your math class again.

You notice that the relationship for the sine function involves the length of the side opposite the angle divided by the length of the hypotenuse. But while the hypotenuse is always a positive number, the sign of the opposite side can be different, depending on what quadrant the angle is drawn in.
::您注意到正弦函数的关系包含对面角的长度,而角则除以下限长度。但是,当下限始终是一个正数时, 反面的符号可能不同, 取决于角的大小。

Can you determine what the sign of the sine function will be in each of the four quadrants, based on the knowledge of the ratio that defines the sine function?
::您能否根据对确定正弦函数的比值的了解,确定正弦函数在四个四分之一中的每一个的符号是什么?

Domain and Range of Trigonometric Functions
::三角函数的域域和范围

While the trigonometric functions may seem quite different from other functions you have worked with, they are in fact just like any other function. We can think of a trig function in terms of “input” and “output.” The input is always an angle. The output is a ratio of sides of a triangle. If you think about the trig functions in this way, you can define the domain and range of each function.
::三角函数可能看起来与您工作过的其他函数大不相同, 但事实上它们与其它函数一样。我们可以从“ 投入” 和“ 产出” 的角度来思考三角函数。输入总是一个角度。输出是三角形边的比。如果您以这种方式思考三角函数, 您可以定义每个函数的域和范围。

Let’s first consider the functions. The input of each of these functions is always an angle, and as you learned in the previous sections, these angles can take on any real number value. Therefore the sine and cosine function have the same domain, the set of all real numbers, $\begin{aligned} R \end{aligned}$ . We can determine the range of the functions if we think about the fact that the sine of an angle is the $\begin{aligned} y - \end{aligned}$ coordinate of the point where the terminal side of the angle intersects the unit circle . The cosine is the $\begin{aligned} x - \end{aligned}$ coordinate of that point. Now recall that in the unit circle, we defined the trig functions in terms of a triangle with hypotenuse 1.
::让我们首先考虑函数。这些函数的输入始终是一个角度, 正如您在前几节中所学到的, 这些角度可以吸收任何实际数字值。因此正弦和余弦函数具有相同的域, 即所有实际数字的一组, R。如果我们想一想一个角的正弦是角的末端交叉单位圆的点的Y- 坐标, 我们就可以确定函数的范围。共弦和余弦函数是该点的x- 坐标。现在请注意, 在单位圆中, 我们用一个三角形来定义三重函数, 有负值 1 的三角形。

In this right triangle, $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ are the lengths of the legs of the triangle, which must have lengths less than 1, the length of the hypotenuse. Therefore the ranges of the sine and cosine function do not include values greater than one. The ranges do, however, contain negative values. Any angle whose terminal side is in the third or fourth quadrant will have a negative $\begin{aligned} y - \end{aligned}$ coordinate, and any angle whose terminal side is in the second or third quadrant will have a negative $\begin{aligned} x - \end{aligned}$ coordinate.
::在此右三角形中, x 和 y 是三角形腿的长度, 其长度必须小于 1, 下限的长度。因此正弦和余弦函数的范围不包括大于1的值。但是, 范围包含负值。任何角度, 其末端位于第三或第四象方, 其末端在第二或第三象方, 其末端在第二或第三象方, 其末端将具有负 X- 相坐标。

In either case, the minimum value is -1. For example, $\begin{aligned} \cos 180^{\circ} = - 1 \end{aligned}$ and $\begin{aligned} \sin 270^{\circ} = - 1 \end{aligned}$ . Therefore the sine and cosine function both have range from -1 to 1.
::任何一种情况下,最低值为-1。例如,cos1801和sin2701。因此,正弦和余弦的功能都介于-1至1之间。

The table below summarizes the domains and ranges of these functions:
::下表概述了这些职能的领域和范围:

	Domain	Range
Sine	$\begin{aligned} θ = R \end{aligned}$	$\begin{aligned} - 1 \leq y \leq 1 \end{aligned}$
Cosine	$\begin{aligned} θ = R \end{aligned}$	$\begin{aligned} - 1 \leq y \leq 1 \end{aligned}$

Knowing the domain and range of the cosine and sine function can help us determine the domain and range of the secant and cosecant function. First consider the sine and cosecant functions, which as we showed above, are reciprocals. The cosecant function will be defined as long as the sine value is not 0. Therefore the domain of the cosecant function excludes all angles with sine value 0, which are $\begin{aligned} 0^{\circ} \end{aligned}$ , $\begin{aligned} 180^{\circ} \end{aligned}$ , $\begin{aligned} 360^{\circ} \end{aligned}$ , etc.
::了解正弦和正弦函数的域和范围可以帮助我们确定分离和余弦函数的域和范围。首先考虑正弦和共弦函数, 正如我们上面所显示的, 它们是对等的。共弦函数将被定义, 只要正弦值不是 0 。因此, 共正弦函数的域排除了正弦值0 的所有角度, 它们是 0, 180, 360等。

In Chapter 2 you will analyze the graphs of these functions, which will help you see why the reciprocal relationship results in a particular range for the cosecant function. Here we will state this range, and in the review questions you will explore values of the sine and cosecant function in order to begin to verify this range, as well as the domain and range of the secant function.
::您将在第二章分析这些函数的图表, 这将帮助您理解为什么对等关系会给余生函数带来一个特定的范围。在此我们将说明这个范围, 并在审查中询问您将探索正弦和余生函数的值, 以便开始验证这个范围, 以及分离函数的域和范围。

	Domain	Range
Cosecant	$\begin{aligned} θ ϵ R, θ \neq 0, 180, 360 \dots \end{aligned}$	$\begin{aligned} \csc θ \leq - 1 \end{aligned}$ or $\begin{aligned} \csc θ \geq 1 \end{aligned}$
Secant	$\begin{aligned} θ ϵ R, θ \neq 90, 270, 450 \dots \end{aligned}$	$\begin{aligned} \sec θ \leq - 1 \end{aligned}$ or $\begin{aligned} \sec θ \geq 1 \end{aligned}$

Now let’s consider the tangent and cotangent functions. The tangent function is defined as $\begin{aligned} \tan θ = \frac{y}{x} \end{aligned}$ . Therefore the domain of this function excludes angles for which the ordered pair has an $\begin{aligned} x - \end{aligned}$ coordinate of $\begin{aligned} 0 : 90^{\circ}, 270^{\circ} \end{aligned}$ , etc. The cotangent function is defined as $\begin{aligned} \cot θ = \frac{x}{y} \end{aligned}$ , so this function’s domain will exclude angles for which the ordered pair has a $\begin{aligned} y - \end{aligned}$ coordinate of $\begin{aligned} 0 : 0^{\circ} \end{aligned}$ , $\begin{aligned} 180^{\circ} \end{aligned}$ , $\begin{aligned} 360^{\circ} \end{aligned}$ , etc.
::现在让我们来考虑正切和余切函数。正切函数被定义为 tan_ yx 。因此, 此函数的域排除了定单对的 X 坐标为 0: 90\ 270\ 等的角。余切函数被定义为 cot_ xy, 因此此函数的域将排除定单对的 Y 坐标为 0: 0\ 、 180\ 、 360 等的角。

Function	Domain	Range
Tangent	$\begin{aligned} θ ϵ R, θ \neq 90, 270, 450 \dots \end{aligned}$	All reals
Cotangent	$\begin{aligned} θ ϵ R, θ \neq 0, 180, 360 \dots \end{aligned}$	All reals

Knowing the ranges of these functions tells you the values you should expect when you determine the value of a trig function of an angle. However, for many problems you will need to identify the sign of the function of an angle: Is it positive or negative?
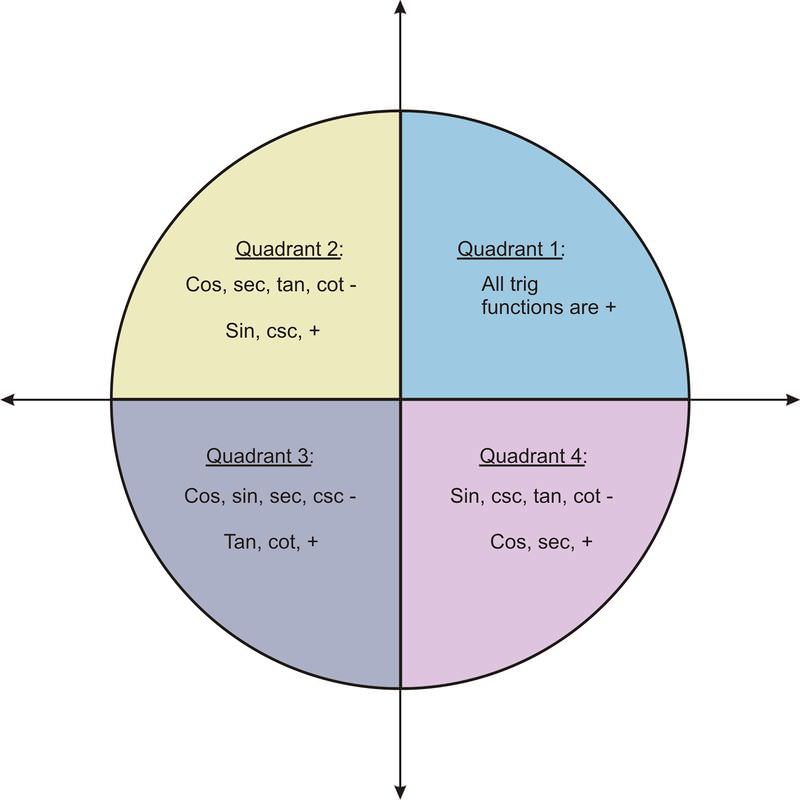
::了解这些函数的范围可以告诉您在确定角的三角函数值时应该期望的值。但是,对于许多问题,您需要识别角函数的符号:是正函数还是负函数?

In determining the ranges of the sine and cosine functions above, we began to categorize the signs of these functions in terms of the quadrants in which angles lie. The figure below summarizes the signs for angles in all 4 quadrants.
::在确定上述正弦和共弦函数的范围时,我们开始将这些函数的标记按角度所在的四角进行分类。下图概述了所有四个四角的角的标记。

An easy way to remember this is “ A ll S tudents T ake C alculus”. Quadrant I: A ll values are positive, Quadrant II: S ine is positive, Quadrant III: T angent is positive, and Quadrant IV: C osine is positive. This simple memory device will help you remember which trig functions are positive and where.
::记住这一点的简单方法就是“所有学生都接受计算”。 Quadrant I:所有价值观都是积极的,Quadrant II:Sine是积极的,Quadrant III:Tangent是积极的,Quadrant IV:Cosine是积极的。这个简单的内存设备可以帮助您记住哪些三角函数是积极的,哪些是积极的。

Stating the Sign
::标注符号

1. State the sign of $\begin{aligned} \cos 100^{\circ} \end{aligned}$
::1. 写上Cos100的标志。

The angle $\begin{aligned} 100^{\circ} \end{aligned}$ is in the second quadrant. Therefore the $\begin{aligned} x - \end{aligned}$ coordinate is negative and so $\begin{aligned} \cos 100^{\circ} \end{aligned}$ is negative.
::角 100位于第二个象限。因此x- 坐标是负的, 所以cos 100是负的。

2. State the sign of $\begin{aligned} \csc 220^{\circ} \end{aligned}$
::2. 写上 csc220 的符号

The angle $\begin{aligned} 220^{\circ} \end{aligned}$ is in the third quadrant. Therefore the $\begin{aligned} y - \end{aligned}$ coordinate is negative. So the sine, and the cosecant are negative.
::角度 220 是在第三个象限中。因此, y - 坐标是负的。因此正弦和 cosecant 是负的。

3. State the sign of $\begin{aligned} \tan 370^{\circ} \end{aligned}$
::3. 写上Tan370的牌子

The angle $\begin{aligned} 370^{\circ} \end{aligned}$ is in the first quadrant. Therefore the tangent value is positive.
::角度 370 位于第一个象限。因此正切值为正值。

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine what the sign of the sine function will be in each of the four quadrants.
::早些时候,有人要求你确定在四个四分位数中的每一个中,正弦函数的标志是什么。

Since the sine function is defined to be the length of the opposite side divided by the length of the hypotenuse, the sign of the sine function is the sign of the $\begin{aligned} y \end{aligned}$ - coordinate for whatever quadrant is being considered. In quadrants 1 and 2, the "y" coordinate is positive, so the sine function is positive. In quadrants 3 and 4, the $\begin{aligned} y \end{aligned}$ - coordinate is negative, so the sine function is negative as well.
::由于正弦函数的定义是正弦函数的长度除以负数长度,正弦函数的标志是正弦函数的Y-坐标符号,无论考虑的象限是什么。在等分1和2中,“y”坐标是正的,因此正弦函数是正的。在等分3和4中,y坐标是负的,因此正弦函数也是负的。

Example 2
::例2

State the sign of $\begin{aligned} \cos 70^{\circ} \end{aligned}$
::国家标志 COS70

The angle $\begin{aligned} 70^{\circ} \end{aligned}$ is in the first quadrant. Cosine is defined to be the adjacent side divided by the hypotenuse. Since the hypotenuse of the unit circle is one and the adjacent side is the $\begin{aligned} x \end{aligned}$ - coordinate, the sign of the cosine function is determined by the sign of the $\begin{aligned} x \end{aligned}$ - coordinate. Since $\begin{aligned} 70^{\circ} \end{aligned}$ is in the first quadrant, the $\begin{aligned} x \end{aligned}$ value is positive. Therefore the cosine value is positive.
::角度 70\\\\ 位于第一个象限。共弦被定义为相邻的侧面, 由下限分隔。由于单位圆的下限为一, 相邻的侧面为x坐标, 余弦函数的符号由 x 坐标符的符号决定。由于共弦函数的符号在第一个象限中为 70\ , x 值为正值。因此, 共弦值为正值。

Example 3
::例3

State the sign of $\begin{aligned} \sin 130^{\circ} \end{aligned}$
::国家是罪的标志... 130... 130...

The angle $\begin{aligned} 130^{\circ} \end{aligned}$ is in the second quadrant. Sine is defined to be the opposite side divided by the hypotenuse. Since the hypotenuse of the unit circle is one and the opposite side is the $\begin{aligned} y \end{aligned}$ -coordinate, the sign of the sine function is determined by the sign of the $\begin{aligned} y \end{aligned}$ - coordinate. Since $\begin{aligned} 130^{\circ} \end{aligned}$ is in the second quadrant, the $\begin{aligned} y \end{aligned}$ value is positive. Therefore the sine value is positive.
::角度 130 位于第二个象限中。 Sine 被定义为由下限除以的对面。由于单位圆的下限为一, 而反面为 Y 坐标, 正弦函数的符号由 y 坐标的符号决定。由于 130 位于第二个象限中, y 值为正值。因此正弦值为正值。

Example 4
::例4

State the sign of $\begin{aligned} \tan 250^{\circ} \end{aligned}$
::国家标志 tan 250

The angle $\begin{aligned} 250^{\circ} \end{aligned}$ is in the third quadrant. Tangent is defined to be the opposite side divided by the adjacent side. In the third quadrant, the $\begin{aligned} x \end{aligned}$ values are negative, and the $\begin{aligned} y \end{aligned}$ values are negative. A negative divided by a negative equals a positive. Therefore the tangent of $\begin{aligned} 250^{\circ} \end{aligned}$ is positive.
::角度 250 位于第三个象限中。 Tangent 被定义为相邻的对面。在第三个象限中, x 值为负, Y 值为负。负除以负等于正。因此, 相切值 250 为正。

Review
::回顾

In what quadrants is the sine function positive?
::在什么条件中,必要功能是积极的?

In what quadrants is the cotangent function negative?
::余分函数负的四分位数是什么?

In what quadrants is the cosine function negative?
::余弦功率在什么四分位数中是负的?

In what quadrants is the tangent function positive?
::相切函数在什么四分位数中是积极的?

For what angles is the cosecant function undefined?
::对于什么角度, COsecant 函数未定义 ?

State the sign of $\begin{aligned} \sin 510^{\circ} \end{aligned}$ .
::国家标志... ...510... ...510...

State the sign of $\begin{aligned} \cos 315^{\circ} \end{aligned}$ .
::国家标志 COS315。

State the sign of $\begin{aligned} \tan 135^{\circ} \end{aligned}$ .
::国家标志丹・135・・・・・・・・・・・・・・・・・

State the sign of $\begin{aligned} \cot 220^{\circ} \end{aligned}$ .
::国家标志 COT220。

State the sign of $\begin{aligned} \csc 40^{\circ} \end{aligned}$ .
::国家标志是csc40\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

State the sign of $\begin{aligned} \cos 330^{\circ} \end{aligned}$ .
::国家标志 COS330。

State the sign of $\begin{aligned} \sin 60^{\circ} \end{aligned}$ .
::国家是罪的象征60年。

State the sign of $\begin{aligned} \sec - 45^{\circ} \end{aligned}$ .
::国家标志秒 -45\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Explain why the cosecant function is never equal to 0.
::解释为什么共生函数从不等于0。

Using your knowledge of domain and range, make a possible sketch for $\begin{aligned} y = \sin x \end{aligned}$ .
::使用您对域和范围的知识, 为 y=sinx 绘制一个草图。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

三角函数的域域、 范围及符号

Domain and Range of Trigonometric Functions ::三角函数的域域和范围

Stating the Sign ::标注符号

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)