6.7

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节闪石

  折叠 展开

  闪石

  播放段落

  Kites
  ::闪石

  播放段落

  A is a quadrilateral with two distinct sets of adjacent congruent sides. It looks like a kite that flies in the air.
  ::A 是一个四边形,有两组不同的相邻相近相近面。 它看起来像一只在空中飞翔的风筝。

  

  播放段落

  From the definition, a kite could be concave . If a kite is concave, it is called a dart. The word distinct in the definition means that the two pairs of congruent sides have to be different. This means that a square or a rhombus is not a kite.
  ::从定义上看,风筝可能是骗局。如果风筝是骗局,它就被称为飞镖。定义中不同的词意味着对立方的对立方必须不同。这意味着广场或暴风车不是风筝。

  播放段落

  The angles between the congruent sides are called vertex angles. The other angles are called non-vertex angles. If we draw the diagonal through the vertex angles, we would have two .
  ::相近面之间的角被称为顶点角度。其他角度则称为非顶点角度。如果我们通过顶点角度绘制对角,我们就会有两个角度。

  

  播放段落

  Facts about Kites
  ::Kites 的真相

  播放段落

  1. The non-vertex angles of a kite are congruent.
  ::1. 风筝的非垂直角度是相同的。

  播放段落

  If $\begin{align*}KITE\end{align*}$ is a kite, then $\begin{align*}\angle K \cong \angle T\end{align*}$ .
  ::如果KITE是风筝,那么KKT。

  播放段落

  2. The diagonal through the vertex angles is the angle bisector for both angles.
  ::2. 通过顶端角的对角线是两个角的角对角。

  播放段落

  If $\begin{align*}KITE\end{align*}$ is a kite, then $\begin{align*}\angle KEI \cong \angle IET\end{align*}$ and $\begin{align*}\angle KIE \cong \angle EIT\end{align*}$ .
  ::如果KITE是风筝 那么KEIIET和KIEIT。

  播放段落

  3.  Kite Diagonals Theorem : The diagonals of a kite are perpendicular .
  ::3. Kite Diagonals理论:风筝的对角是垂直的。

  播放段落

  $\begin{align*}\triangle KET\end{align*}$ and $\begin{align*}\triangle KIT\end{align*}$ are , so $\begin{align*}\overline{EI}\end{align*}$ is the perpendicular bisector of $\begin{align*}\overline{KT}\end{align*}$ ( Isosceles Triangle Theorem).
  ::KET和KIT是,所以EI是'KT(岛屿三角理论)的直角两侧部分。

  播放段落

  What if you were told that $\begin{align*}WIND\end{align*}$ is a kite and you are given information about some of its angles or its diagonals? How would you find the measure of its other angles or its sides?
  ::假若有人对你们说:WINDIS是一个风筝,而且你们获得关于它的一些角度或对角的信息,那末,你们怎么发现它的其他角度或侧面的尺寸呢?

  播放段落

  Examples
  ::实例

  播放段落

  For Examples 1 and 2, use the following information:
  ::关于例1和例2,请使用以下信息:

  播放段落

  $\begin{align*}KITE\end{align*}$ is a kite.
  ::KITE是风筝。

  

  播放段落

  Example 1
  ::例1

  播放段落

  Find  $\begin{align*}m \angle KIS\end{align*}$ .
  ::去找玛姬丝

  播放段落

  $\begin{align*}m\angle KIS=25^\circ\end{align*}$ by the Triangle Sum Theorem (remember that $\begin{align*}\angle KSI\end{align*}$ is a right angle because the diagonals are perpendicular.)
  ::MKIS=25 by the Triangle SumTheorem (记住KSI是一个正确角度, 因为对角是垂直的 。 )

  播放段落

  Example 2
  ::例2

  播放段落

  Find  $\begin{align*}m \angle IST\end{align*}$ .
  ::找到密西西比州

  播放段落

  $\begin{align*}m\angle IST=90^\circ\end{align*}$ because the diagonals are perpendicular.
  ::máIST=90 因为对角是垂直的

  播放段落

  Example 3
  ::例3

  播放段落

  Find the missing measures in the kites below.
  ::在下面的风筝中找出缺失的测量方法。

  1. 

  播放段落

   The two angles left are the non-vertex angles, which are congruent.
  ::左两个角度是非垂直角度,它们相近。

  播放段落

  $$\begin{align*}130^\circ + 60^\circ + x + x & = 360^\circ\\ 2x & = 170^\circ\\ x & = 85^\circ \qquad \text{Both angles are}\ 85^\circ.\end{align*}$$
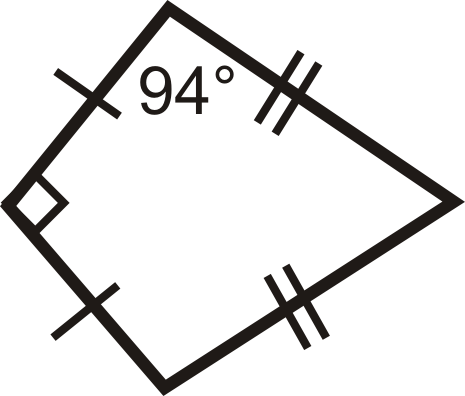
  ::13060x+x=3602x=170x=85BOT角度为85。

  2. 

  播放段落

   The other non-vertex angle is also $\begin{align*}94^\circ\end{align*}$ . To find the fourth angle, subtract the other three  angles from $\begin{align*}360^\circ\end{align*}$ .
  ::其它非垂直角度也是 94 。 要找到第四个角度, 请从 360 中减去其他三个角度 。

  播放段落

  $$\begin{align*}90^\circ + 94^\circ + 94^\circ + x & = 360^\circ\\ x & = 82^\circ\end{align*}$$
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}九九九四一四一四一x=三六○一x=八二* {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}九九九四一四一四一x=三百零一x=三百零一xx=八二

  播放段落

  Example 4
  ::例4

  播放段落

  Use to find the lengths of the sides of the kite.
  ::用它来找到风筝两侧的长度。

  

  播放段落

  Recall that the Pythagorean Theorem says $\begin{align*}a^2 + b^2 = c^2\end{align*}$ , where $\begin{align*}c\end{align*}$ is the hypotenuse . In this kite, the sides are the hypotenuses.
  ::记得毕达哥里安神话中写着a2+b2=c2, c是下限。在这个风筝中, 侧面是下限 。

  播放段落

  $$\begin{align*}6^2 + 5^2 & = h^2 && 12^2 + 5^2 = j^2\\ 36 + 25 & = h^2 && 144 + 25 = j^2\\ 61 & = h^2 && \qquad \ 169 = j^2\\ \sqrt{61} & = h && \qquad \quad 13 = j\end{align*}$$
  ::62+52=h2122+52=j236+25=h2144+25=j261=h2 169=j2_61=h13=j

  播放段落

  Example 5
  ::例5

  播放段落

  Prove that the non-vertex angles of a kite are congruent.
  ::证明风筝的非垂直角度是相同的。

  播放段落

  Given : $\begin{align*}KITE\end{align*}$ with $\begin{align*}\overline{KE} \cong \overline{TE}\end{align*}$ and $\begin{align*}\overline{KI} \cong \overline{TI}\end{align*}$
  ::基蒂和凯蒂

  播放段落

  Prove : $\begin{align*}\angle K \cong \angle T\end{align*}$
  ::证明: @KT

  

  Statement	Reason
  1. $\begin{align*}\overline{KE} \cong \overline{TE}\end{align*}$ and $\begin{align*}\overline{KI} \cong \overline{TI}\end{align*}$	1. Given
  2. $\begin{align*}\overline{EI} \cong \overline{EI}\end{align*}$	2. Reflexive PoC
  3. $\begin{align*}\triangle EKI \cong \triangle ETI\end{align*}$	3.
  4. $\begin{align*}\angle K \cong \angle T\end{align*}$	4.

  播放段落

  Review
  ::回顾

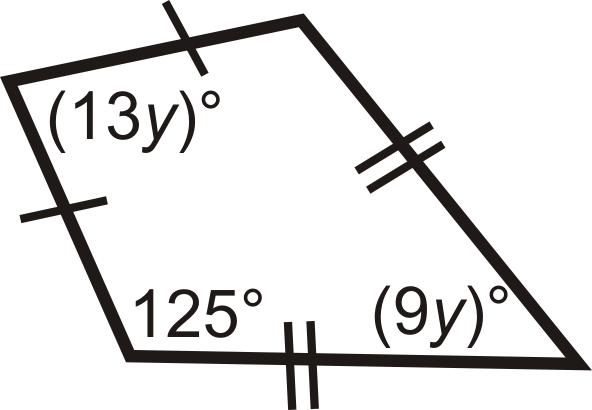
  播放段落

  For questions 1-6, find the value of the missing variable(s). All figures are kites.
  ::对于问题1-6,请查找缺失变量的价值。所有数字均为风筝。

  1. 
  2. 
  3. 
  4. 
  5. 
  6. 

  播放段落

  For questions 7-11, find the value of the missing variable(s).
  ::对于问题7-11,请找到缺失变量的价值。

  7. 
  8. 
  9. 
  10. 
  11. 

  播放段落
  12. Fill in the blanks to the proof below.
      ::将空白填充到以下的证明上。

  播放段落

  Given : $\begin{align*}\overline{KE} \cong \overline{TE}\end{align*}$ and $\begin{align*}\overline{KI} \cong \overline{TI}\end{align*}$
  ::基於:"可以"和"可以"

  播放段落

  Prove : $\begin{align*}\overline{EI}\end{align*}$ is the angle bisector of $\begin{align*}\angle KET\end{align*}$ and $\begin{align*}\angle KIT\end{align*}$
  ::证明:"我"是"KET"和"KIT"的分角

  

  Statement	Reason
  1. $\begin{align*}\overline{KE} \cong \overline{TE}\end{align*}$ and $\begin{align*}\overline{KI} \cong \overline{TI}\end{align*}$	1.
  2. $\begin{align*}\overline{EI} \cong \overline{EI}\end{align*}$	2.
  3. $\begin{align*}\triangle EKI \cong \triangle ETI\end{align*}$	3.
  4.	4. CPCTC
  5. $\begin{align*}\overline{EI}\end{align*}$ is the angle bisector of $\begin{align*}\angle KET\end{align*}$ and $\begin{align*}\angle KIT\end{align*}$	5.

  播放段落
  13. Fill in the blanks to the proof below.
      ::将空白填充到以下的证明上。

  播放段落

  Given : $\begin{align*}\overline{EK} \cong \overline{ET}, \overline{KI} \cong \overline{IT}\end{align*}$
  ::基於:

  播放段落

  Prove : $\begin{align*}\overline{KT} \bot \overline{EI}\end{align*}$
  ::证明:

  

  Statement	Reason
  1. $\begin{align*}\overline{KE} \cong \overline{TE}\end{align*}$ and $\begin{align*}\overline{KI} \cong \overline{TI}\end{align*}$	1.
  2.	2. Definition of isosceles triangles
  3. $\begin{align*}\overline{EI}\end{align*}$ is the angle bisector of $\begin{align*}\angle KET\end{align*}$ and $\begin{align*} \angle KIT\end{align*}$	3.
  4.	4. Isosceles Triangle Theorem
  5. $\begin{align*}\overline{KT} \bot \overline{EI}\end{align*}$	5.

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。