课程： 6.8 四方分类 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节四方分类

折叠展开
四方分类
Classifying Quadrilaterals
::分类四边债

When working in the coordinate plane , you will sometimes want to know what type of shape a given shape is. You should easily be able to tell that it is a quadrilateral if it has four sides. But how can you classify it beyond that?
::当您在坐标平面上工作时, 您有时会想知道给定形状的形状是什么类型。您应该很容易地知道它是一个四边形, 如果它有四边形的话。但是, 您如何将它分类到此以外呢 ?

First you should graph the shape if it has not already been graphed. Look at it and see if it looks like any special quadrilateral. Do the sides appear to be congruent ? Do they meet at right angles ? This will give you a place to start.
::首先,您应该绘制形状图, 如果尚未绘制图形的话。看看它, 看看它是否像任何特殊的四边形。边是否相似? 它们是否在正确的角度相遇 ? 这将为您提供一个起始位置。

Once you have a guess for what type of quadrilateral it is, your job is to prove your guess. To prove that a quadrilateral is a , rectangle , rhombus , square , or trapezoid , you must show that it meets the definition of that shape OR that it has properties that only that shape has.
::一旦你猜到它是什么类型的四边形,你的工作就是证明你的猜想。要证明一个四边形是一个、矩形、正方形、正方形或形,你就必须证明它符合该形状的定义,或者它有只有形状才有的属性。

If it turns out that your guess was wrong because the shape does not fulfill the necessary properties, you can guess again. If it appears to be no type of special quadrilateral then it is simply a quadrilateral .
::如果结果发现你的猜测是错误的, 因为形状不能满足必要的属性, 您可以再次猜测。如果它看起来不是特殊四边形, 那么它只是一个四边形。

The examples below will help you to see what this process might look like.
::下面的例子将有助于你们了解这一进程可能是什么样子。

What if you were given the coordinates of four points that form a quadrilateral? How could you determine if that quadrilateral qualifies as one of the special four-sided figures you learned about in the previous sections?
::如果你们获得构成四边形的四个点的座标呢?你如何确定四边形是否适合作为你们在前几节中了解到的特别四面数字之一?

Examples
::实例

Example 1
::例1

A quadrilateral is defined by the four lines $\begin{aligned} y = 2 x + 1 \end{aligned}$ , $\begin{aligned} y = - 2 x + 5 \end{aligned}$ , $\begin{aligned} y = 2 x - 4 \end{aligned}$ , and $\begin{aligned} y = - 2 x - 5 \end{aligned}$ . Is this quadrilateral a rectangle?
::四边形由四行 y= 2x+1, y2x+5, y= 2x-4和y2x-5. 定义。四边形是矩形吗?

To be a rectangle a shape must have four right angles. This means that the sides must be perpendicular to each other. From the given equations we see that the slopes are $\begin{aligned} 2 \end{aligned}$ , $\begin{aligned} - 2 \end{aligned}$ , $\begin{aligned} 2 \end{aligned}$ and $\begin{aligned} - 2 \end{aligned}$ . Because the slopes are not opposite reciprocals of each other, the sides are not perpendicular, and the shape is not a rectangle.
::要成为矩形矩形,形状必须具有四个右角度。这意味着两边必须相互垂直。从给定的方程式中,我们看到斜坡是2,2-2,2和-2。因为斜坡不是对等的,两边不是对等的,两边不是对立的,形状也不是矩形。

Example 2
::例2

Determine what type of quadrilateral $\begin{aligned} A B C D \end{aligned}$ is: $\begin{aligned} A (- 3, 3), B (1, 5), C (4, - 1), D (1, - 5) \end{aligned}$ .
::确定A(-3),3,B(1,5),C(4,-1),D(1,-5),D(1,5)四边形ABCD的类型。

First, graph $\begin{aligned} A B C D \end{aligned}$ . This will make it easier to figure out what type of quadrilateral it is. From the graph, we can tell this is not a parallelogram. Find the slopes of $\begin{aligned} \bar{B C} \end{aligned}$ and $\begin{aligned} \bar{A D} \end{aligned}$ to see if they are parallel .
::首先, 图 ABCD 。这样可以更容易地找出它是哪类四边形。从图表中, 我们可以看到这不是一个平行图。找到 BC 的斜坡, 然后自动查看它们是否平行。

Slope of $\begin{aligned} \bar{B C} = \frac{5 - (- 1)}{1 - 4} = \frac{6}{- 3} = - 2 \end{aligned}$
::BC 5 - (-1)1 - 4= 6 - 3 *2

Slope of $\begin{aligned} \bar{A D} = \frac{3 - (- 5)}{- 3 - 1} = \frac{8}{- 4} = - 2 \end{aligned}$
::AD 3 - (-5) - (-)3 - 1=8 - 42

$\begin{aligned} \bar{B C} ‖ \bar{A D} \end{aligned}$ , so $\begin{aligned} A B C D \end{aligned}$ is a trapezoid. To determine if it is an isosceles trapezoid , find $\begin{aligned} A B \end{aligned}$ and $\begin{aligned} C D \end{aligned}$ .
::BC 'AD',所以ABCD是一个陷阱类。要确定它是否是一个等骨类,请找到AB和CD。

$\begin{aligned} A B & = \sqrt{(- 3 - 1)^{2} + (3 - 5)^{2}} & S T = \sqrt{(4 - 1)^{2} + (- 1 - (- 5))^{2}} \\ = \sqrt{(- 4)^{2} + (- 2)^{2}} & = \sqrt{3^{2} + 4^{2}} \\ = \sqrt{20} = 2 \sqrt{5} & = \sqrt{25} = 5 \end{aligned}$

::AB=(-3--1)2+(3-5)2+(3-5)2ST=(4-1)2+(-1)2+(-1-(-5))2=(-4)2+(-2)2+(-2)2=(32+42=20=25=25=5)

$\begin{aligned} A B \neq C D \end{aligned}$ , therefore this is not an isosceles trapezoid.
::ABQCD, 因此这不是一个等离子细胞类。

Example 3
::例3

Determine what type of quadrilateral $\begin{aligned} E F G H \end{aligned}$ is: $\begin{aligned} E (5, - 1), F (11, - 3), G (5, - 5), H (- 1, - 3) \end{aligned}$ .
::确定哪种四边形的EFGH是:E(5)-5,F(11)-3,G(5)-5,H(-1)-3。

We will not graph this example. Let’s find the length of all four sides.
::我们不会以此为例。让我们看看四面的长度。

$\begin{aligned} E F & = \sqrt{(5 - 11)^{2} + (- 1 - (- 3))^{2}} & F G = \sqrt{(11 - 5)^{2} + (- 3 - (- 5))^{2}} \\ = \sqrt{(- 6)^{2} + 2^{2}} = \sqrt{40} & = \sqrt{6^{2} + 2^{2}} = \sqrt{40} \\ G H & = \sqrt{(5 - (- 1))^{2} + (- 5 - (- 3))^{2}} & H E = \sqrt{(- 1 - 5)^{2} + (- 3 - (- 1))^{2}} \\ = \sqrt{6^{2} + (- 2)^{2}} = \sqrt{40} = 2 \sqrt{10} & = \sqrt{(- 6)^{2} + (- 2)^{2}} = \sqrt{40} = 2 \sqrt{10} \end{aligned}$

::EF = (5- 11)2+(-1- (3))2 FG = (11- 5)2 FG = (3- (5)2+ (6)2+22= 40 = 62+22= 40GH= (5- (1))2+(5- (3))2+2HE= (-1)5-2)2+(-3- (3- (1)))2+(-3-2)2= 62+(-2)2= 40= 210=(-6)2+(-2)2=40=210

All four sides are equal. This quadrilateral is either a rhombus or a square . Let’s find the length of the diagonals .
::四面是平等的。这四边是圆柱或方形。让我们来看看对角线的长度。

$\begin{aligned} E G & = \sqrt{(5 - 5)^{2} + (- 1 - (- 5))^{2}} & F H = \sqrt{(11 - (- 1))^{2} + (- 3 - (- 3))^{2}} \\ = \sqrt{0^{2} + 4^{2}} & = \sqrt{12^{2} + 0^{2}} \\ = \sqrt{16} = 4 & = \sqrt{144} = 12 \end{aligned}$

::EG=(5-5-5)2+(-1-(-5))2FH=(11-(-1))2+(-3-(-3))2+(02+42=122+02=16=4=144=12)2FH=(11-(-1))2+(-3-(-3))2=02+42=122+02=16=4=144=12

The diagonals are not congruent, so $\begin{aligned} E F G H \end{aligned}$ is a rhombus and not a square.
::三角形是不一致的,所以EFGH是一个圆柱形,而不是一个方形。

Example 4
::例4

Determine what type of parallelogram $\begin{aligned} T U N E \end{aligned}$ is: $\begin{aligned} T (0, 10), U (4, 2), N (- 2, - 1) \end{aligned}$ , and $\begin{aligned} E (- 6, 7) \end{aligned}$ .
::确定T(0,10)、U(4,4,2,N(-2,-1)和E(-6,7)是何种类型的平行图图。

This looks like a rectangle. Let’s see if the diagonals are equal. If they are, then $\begin{aligned} T U N E \end{aligned}$ is a rectangle.
::这看起来像一个矩形。让我们看看对角线是否相等。如果是, 那么 TUNE 是一个矩形。

$\begin{aligned} E U & = \sqrt{(- 6 - 4)^{2} + (7 - 2)^{2}} & T N = \sqrt{(0 + 2)^{2} + (10 + 1)^{2}} \\ = \sqrt{(- 10)^{2} + 5^{2}} & = \sqrt{2^{2} + 11^{2}} \\ = \sqrt{100 + 25} & = \sqrt{4 + 121} \\ = \sqrt{125} = 5 \sqrt{5} & = \sqrt{125} = 5 \sqrt{5} \end{aligned}$

::欧盟=(-6-4)2+(7-2)2+(7-2)2TN=(0+2)2+(10+1)2+(10+1)2=(10)2+52=22+112=100+25=4+121=125=55=125=55

If the diagonals are also perpendicular, then $\begin{aligned} T U N E \end{aligned}$ is a square.
::如果对角线也是垂直的,那么TUNE就是一个方形。

$\begin{aligned} Slope of E U = \frac{7 - 2}{- 6 - 4} = - \frac{5}{10} = - \frac{1}{2} Slope of T N = \frac{10 - (- 1)}{0 - (- 2)} = \frac{11}{2} \end{aligned}$
::EU=7-2 - 6 - 4 - 4510 12 斜体TN=10 - (-1)0 - (-2)=112

The slope of $\begin{aligned} E U \neq \end{aligned}$ slope of $\begin{aligned} T N \end{aligned}$ , so $\begin{aligned} T U N E \end{aligned}$ is a rectangle.
::TN的欧经斜坡,所以TUNE是一个矩形。

Example 5
::例5

Determine what type of quadrilateral $\begin{aligned} R S T V \end{aligned}$ is.
::确定哪种类型的四边RSTV。

This looks like a kite. Find the lengths of all the sides to check if the adjacent sides are congruent.
::这看起来像风筝。找出所有边的长度, 检查相邻边是否一致。

$\begin{aligned} R S & = \sqrt{(- 5 - 2)^{2} + (7 - 6)^{2}} & S T = \sqrt{(2 - 5)^{2} + (6 - (- 3))^{2}} \\ = \sqrt{(- 7)^{2} + 1^{2}} & = \sqrt{(- 3)^{2} + 9^{2}} \\ = \sqrt{50} & = \sqrt{90} \end{aligned}$

::RS=(-5-2)2+(7-6)2+(7-6)2ST=(2-5)2+(6-(3-3))2+(6-7)2+12=(3)2+92=50=90

$\begin{aligned} R V & = \sqrt{(- 5 - (- 4))^{2} + (7 - 0)^{2}} & V T = \sqrt{(- 4 - 5)^{2} + (0 - (- 3))^{2}} \\ = \sqrt{(- 1)^{2} + 7^{2}} & = \sqrt{(- 9)^{2} + 3^{2}} \\ = \sqrt{50} & = \sqrt{90} \end{aligned}$

::RV=(-5-(-4))2+(-7-0)2VT=(-4-5)2+(-0-(-3))2+(-0-(-1))2=(-1)2+72=(-9)2+32=50=90

From this we see that the adjacent sides are congruent. Therefore, $\begin{aligned} R S T V \end{aligned}$ is a kite.
::因此,RSTV是风筝。

Review
::回顾

Determine what type of quadrilateral $\begin{aligned} A B C D \end{aligned}$ is.
::确定四边形ABCD是哪种类型。

$\begin{aligned} A (- 2, 4), B (- 1, 2), C (- 3, 1), D (- 4, 3) \end{aligned}$
::A(-2,4),B(-1,2),C(-3,3),D(-4,3)

$\begin{aligned} A (- 2, 3), B (3, 4), C (2, - 1), D (- 3, - 2) \end{aligned}$
::A(2,2、3,B(3,4),C(2,-1),D(-3,-2)

$\begin{aligned} A (1, - 1), B (7, 1), C (8, - 2), D (2, - 4) \end{aligned}$
::A(1)-1,B(7)-1,C(8)-2,D(2)-4)

$\begin{aligned} A (10, 4), B (8, - 2), C (2, 2), D (4, 8) \end{aligned}$
::A(10,4),B(8,8)-2,C(2,2),D(4,8)

$\begin{aligned} A (0, 0), B (5, 0), C (0, 4), D (5, 4) \end{aligned}$
::A(0,0,0,B(5,5,0),C(0,4),D(5,4)

$\begin{aligned} A (- 1, 0), B (0, 1), C (1, 0), D (0, - 1) \end{aligned}$
::A(1,0,0,B(0,0,1),C(1,1,0,D(0,-1))

$\begin{aligned} A (2, 0), B (3, 5), C (5, 0), D (6, 5) \end{aligned}$
::A(2,0,B(3,5,5),C(5,5),D(6,5)

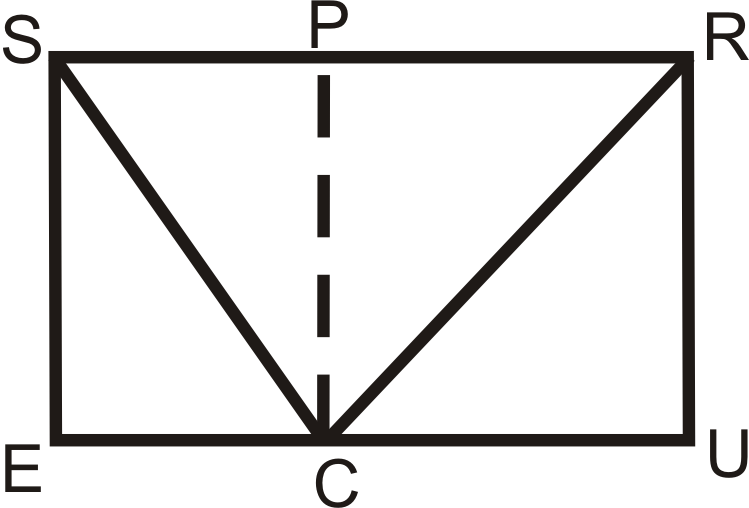
$\begin{aligned} S R U E \end{aligned}$ is a rectangle and $\begin{aligned} P R U C \end{aligned}$ is a square.
::SRUE是一个矩形,PRUC是一个方形。

What type of quadrilateral is $\begin{aligned} S P C E \end{aligned}$ ?
::什么类型的四边形是PCE?

If $\begin{aligned} S R = 20 \end{aligned}$ and $\begin{aligned} R U = 12 \end{aligned}$ , find $\begin{aligned} C E \end{aligned}$ .
::如果SR=20和RU=12,请找到CE。

Find $\begin{aligned} S C \end{aligned}$ and $\begin{aligned} R C \end{aligned}$ based on the information from part b. Round your answers to the nearest hundredth.
::根据 b部分的信息查找SC 和 RC 。将您的答复四舍五入到最接近的第一百个。

For questions 11-14, determine what type of quadrilateral $\begin{aligned} A B C D \end{aligned}$ is. If it is no type of special quadrilateral, just write quadrilateral .
::对于问题11-14, 确定哪类ABCD为四边形。如果不是特殊四边形, 只需写四边形即可。

$\begin{aligned} A (1, - 2), B (7, - 5), C (4, - 8), D (- 2, - 5) \end{aligned}$
::A(1,-2),B(7,-5),C(4,-8),D(-2,-5)

$\begin{aligned} A (6, 6), B (10, 8), C (12, 4), D (8, 2) \end{aligned}$
::A(6,6),B(10,8,8),C(12,4),D(8,2)

$\begin{aligned} A (- 1, 8), B (1, 4), C (- 5, - 4), D (- 5, 6) \end{aligned}$
::A(1,1,8,B(1,4),C(-5,4),D(-5,6)

$\begin{aligned} A (5, - 1), B (9, - 4), C (6, - 10), D (3, - 5) \end{aligned}$
::A(5)-1,B(9)-4,C(6)-10,D(3)-5

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

四方分类

Classifying Quadrilaterals ::分类四边债

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Classifying Quadrilaterals
::分类四边债

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)