7.3 类似的多边形和规模因素
章节大纲
-
Similar Polygons
::类似多边形Similar polygons are two polygons with the same shape, but not the same size. Similar polygons have that are congruent , and corresponding sides that are proportional.
::类似的多边形是两个形状相同但大小不同的多边形。类似的多边形具有相似的相形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形色形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形体形体形体形体形体形体形体形体形体形体形体形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形形形形形形形形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形体形These polygons are not similar :
::这些多边形不相似 :Scale Factors
::比例因素Think about similar polygons as enlarging or shrinking the same shape. The symbol ∼ is used to represent similarity. Specific types of triangles, quadrilaterals, and polygons will always be similar. For example, all are similar and all squares are similar . If two polygons are similar, we know the lengths of corresponding sides are proportional. In similar polygons, the ratio of one side of a polygon to the corresponding side of the other is called the scale factor . The ratio of all parts of a polygon (including the perimeters, diagonals , , midsegments, altitudes) is the same as the ratio of the sides.
::将相似的多边形想象成扩大或缩小相同形状。 符号 __ 用来表示相似性。 特定类型的三角形、 四边形和多边形总是相似的。 例如, 所有的三角形都相似, 所有的方形都相似。 如果两个多边形相似, 我们知道对应边的长度是成比例的。 在类似的多边形中, 多边形的一方与另一边的对应方的比被称为比例系数。 多边形所有部分( 包括周边、 三角形、 中点、 高度) 的比例与两边的比例相同 。What if you were told that two pentagons were similar and you were given the lengths of each pentagon's sides. How could you determine the scale factor of pentagon #1 to pentagon #2?
::如果你被告知两个五角形相似, 并且给您以五角形两边的长度。 您如何确定五角形 1 到五角形 2 的比值 ?Examples
::实例Example 1
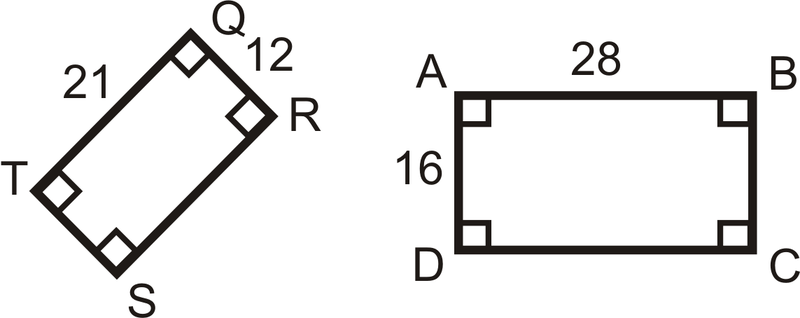
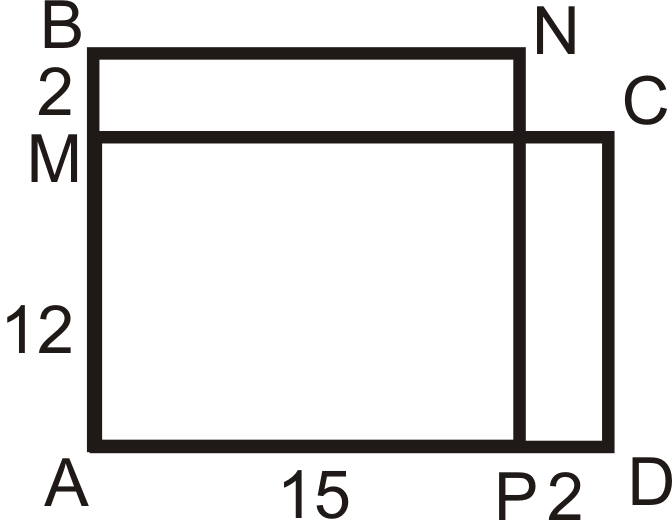
::例1A B C D and U V W X are below. Are these two similar?
::ABCD和UVWX如下。 这两种情况相似吗 ?All the corresponding angles are congruent because the shapes are rectangles.
::所有相应的角度都是相同的, 因为形状是矩形 。Let’s see if the sides are proportional. 8 12 = 2 3 and 18 24 = 3 4 . 2 3 ≠ 3 4 , so the sides are not in the same proportion , and the rectangles are not similar.
::让我们看看两边是否成比例。 812=23和1824=34。 2334, 所以两边的比例不同, 矩形也不相似。Example 2
::例2△ A B C ∼ △ M N P . The perimeter of △ A B C is 150, A B = 32 and M N = 48 . Find the perimeter of △ M N P .
::ABC=MNP. ABC的周界是150,ABB=32和MN=48. 找到ZMNP的周界。From the similarity statement, A B and M N are corresponding sides. The scale factor is 32 48 = 2 3 or 3 2 . △ A B C is the smaller triangle , so the perimeter of △ M N P is 3 2 ( 150 ) = 225 .
::从相似语句中, AB 和 MN 是相应的边。 比例系数为 3248=23 或 32. ABC 是较小的三角形, 所以 QMNP 的周边是 32( 150) = 225 。Example 3
::例3Suppose △ A B C ∼ △ J K L . Based on the similarity statement, which angles are congruent and which sides are proportional?
::假设 ABC JKL. 依据相似性声明,哪些角度是相同的,哪些方面是相称的?Just like in a congruence statement, the congruent angles line up within the similarity statement. So, ∠ A ≅ ∠ J , ∠ B ≅ ∠ K , and ∠ C ≅ ∠ L . Write the sides in a proportion: A B J K = B C K L = A C J L . Note that the proportion could be written in different ways. For example, A B B C = J K K L is also true.
::就像一个一致的语句, 一致的角度在相似的语句中排成一行。 因此, AJ, BK, 和CL. 以一个比例写两边: ABJK=BCKL=ACJL。 请注意, 比例可以用不同的方式写。 例如, ABBC=JKKL 也是真实的 。Example 4
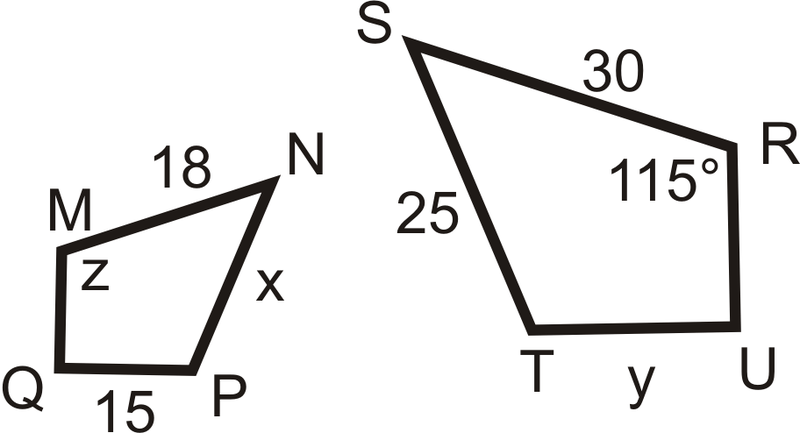
::例4M N P Q ∼ R S T U . What are the values of x , y and z ?
::MNPZRSTU,x,y和z值是多少?In the similarity statement, ∠ M ≅ ∠ R , so z = 115 ∘ . For x and y , set up proportions.
::在相似性说明中, X 和 y 设定比例 。18 30 = x 25 18 30 = 15 y 450 = 30 x 18 y = 450 x = 15 y = 25
::1830=x25 1830=15y450=30x18y=450x=450x=15y=25Example 5
::例5A B C D ∼ A M N P . Find the scale factor and the length of B C .
::ABCDANNP. 找出比例系数和不列颠哥伦比亚的长度。Line up the corresponding sides, A B and A M = C D , so the scale factor is 30 45 = 2 3 or 3 2 . Because B C is in the bigger rectangle , we will multiply 40 by 3 2 because 3 2 is greater than 1. B C = 3 2 ( 40 ) = 60 .
::在相应的边上排列,AB和AM=CD,因此比例系数为3045=23或32。 由于BC位于较大的矩形中,我们将乘以40乘以32, 因为32大于1 BC=32(40)=60。Review
::回顾For questions 1-8, determine whether the following statements are true or false.
::对于问题1-8,确定以下陈述是真实的还是虚假的。-
All equilateral triangles are similar.
::所有等边三角形都相似。 -
All isosceles triangles are similar.
::所有的等分形三角形都相似 。 -
All rectangles are similar.
::所有矩形相似 。 -
All rhombuses are similar.
::{\fnSIMHEI\fs22\1cHFFFFFF\3cHFF8000}所有的丧礼都是相似的 {\fnSIMHEI\fs22\1cHFFFFFF\3cHFF8000}我说过 -
All squares are similar.
::所有广场都相似。 -
All congruent polygons are similar.
::所有相同的多边形都相似。 -
All similar polygons are congruent.
::所有相似的多边形都相似。 -
All regular pentagons are similar.
::所有普通的五边形都相似。 -
△
B
I
G
∼
△
H
A
T
. List the congruent angles and proportions for the sides.
::列出两边的一致角度和比例。 -
If
B
I
=
9
and
H
A
=
15
, find the scale factor.
::如果BI=9和HA=15发现比额表系数。 -
If
B
G
=
21
, find
H
T
.
::如果BG=21,请找到HT。 -
If
A
T
=
45
, find
I
G
.
::如果AT=45,请找到IG -
Find the perimeter of
△
B
I
G
and
△
H
A
T
. What is the ratio of the perimeters?
::找到ZBIG和HAT的周界 周界的比例是多少? -
An NBA basketball court is a rectangle that is 94 feet by 50 feet. A high school basketball court is a rectangle that is 84 feet by 50 feet. Are the two rectangles similar?
::NBA篮球场是94英尺乘50英尺的矩形。 高中篮球场是84英尺乘50英尺的矩形。 两个矩形相似吗? -
HD TVs have sides in a ratio of 16:9. Non-HD TVs have sides in a ratio of 4:3. Are these two ratios equivalent?
::HD电视的侧面比例为16:9. 非HD电视的侧面比例为4:3。 这两个比例是否相等?
Use the picture to the right to answer questions 16-20.
::用照片来表达回答问题16-20的权利。-
Find
m
∠
E
and
m
∠
Q
.
::去找妈妈和妈妈 -
A
B
C
D
E
∼
Q
L
M
N
P
, find the scale factor.
::ABCDELMNP, 找到比例系数 。 -
Find
B
C
.
::寻找 BC 。 -
Find
C
D
.
::查找 CD 。 -
Find
N
P
.
::找到NP。 寻找NP。
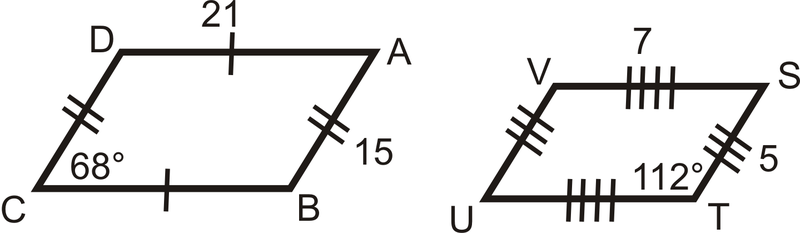
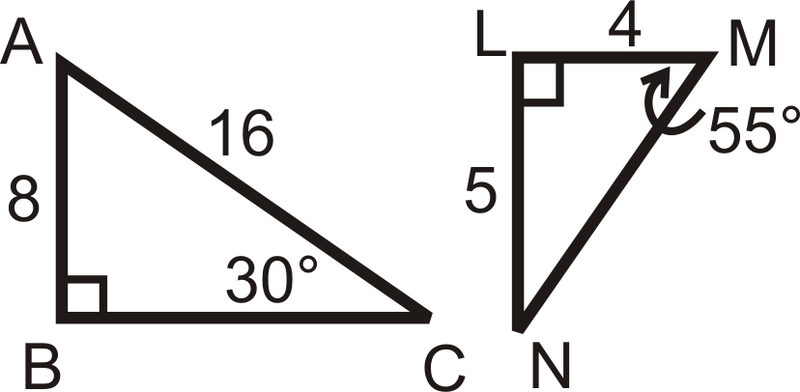
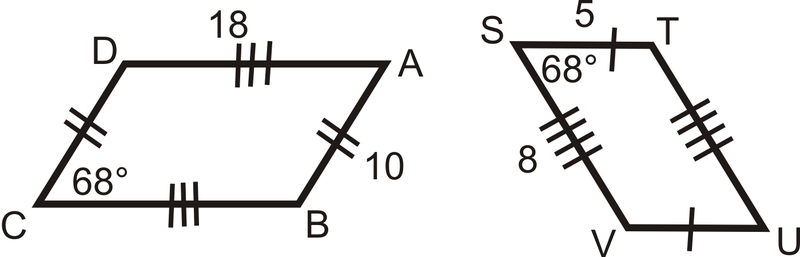
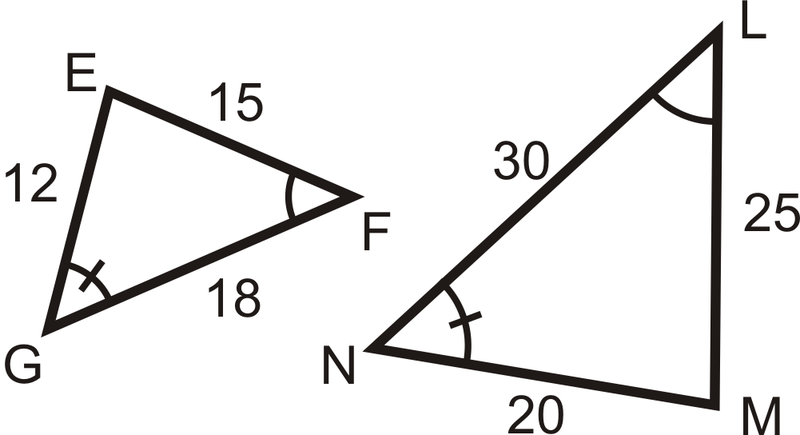
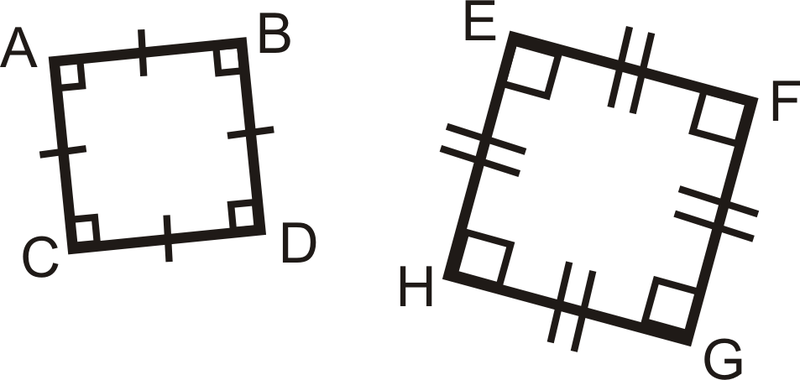
Determine if the following triangles and quadrilaterals are similar. If they are, write the similarity statement.
::确定以下三角形和四边形是否相似。如果相似,请写入相似语句。Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。Resources
::资源 -
All equilateral triangles are similar.