7.4AA 相似性
章节大纲
-
AA Similarity Postulate
::AA 相似性假设By definition, two triangles are similar if all their are congruent and their corresponding sides are proportional. It is not necessary to check all angles and sides in order to tell if two triangles are similar. In fact, if you only know that two pairs of corresponding angles are congruent that is enough information to know that the triangles are similar. This is called the AA Similarity Postulate .
::按定义,如果两个三角形都一致,而相应的两边是成比例的,则两个三角形是相似的。没有必要检查所有角度和边,以判断两个三角形是否相似。事实上,如果你只知道两对对应角度是相近的,这足以说明三角形是相似的。这被称为“ AA 相似性假设 ” 。AA Similarity Postulate: If two angles in one triangle are congruent to two angles in another triangle, then the two triangles are similar.
::AA 相似性假设: 如果一个三角形的两个角度与另一个三角形的两个角度相匹配, 那么两个三角形是相似的 。If ∠ A ≅ ∠ Y and ∠ B ≅ ∠ Z , then △ A B C ∼ △ Y Z X .
::如果"A"Y和"B",那么"ABC"YZX。What if you were given a pair of triangles and the angle measures for two of their angles? How could you use this information to determine if the two triangles are similar?
::如果给了您一对三角形, 并给您两个角的角度量值呢? 您如何使用这些信息来确定这两个三角形是否相似 ?Examples
::实例Example 1
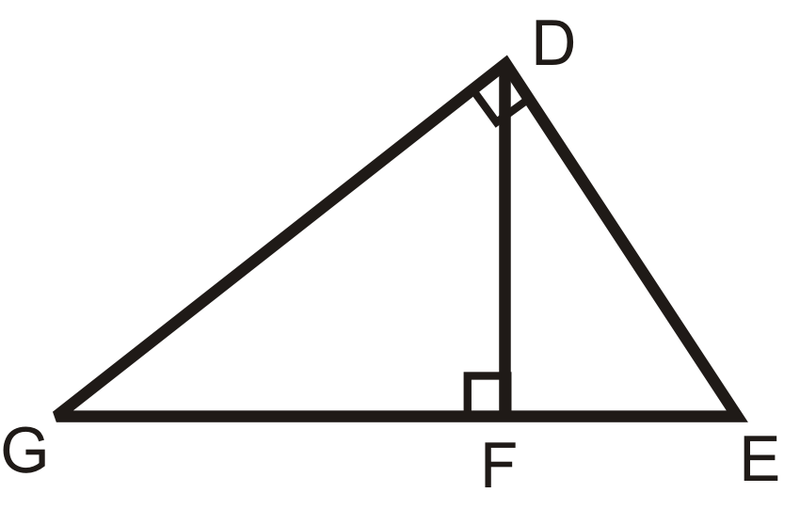
::例1Are the triangles similar? If so, write a similarity statement.
::三角形相似吗 ? 如果是, 请写一个相似语句 。Yes, there are three similar triangles that each have a right angle . D G E ∼ F G D ∼ F D E .
::是的,有三种相似的三角形,每个三角形都有正确的角度。 DGEFGDFDDE。Example 2
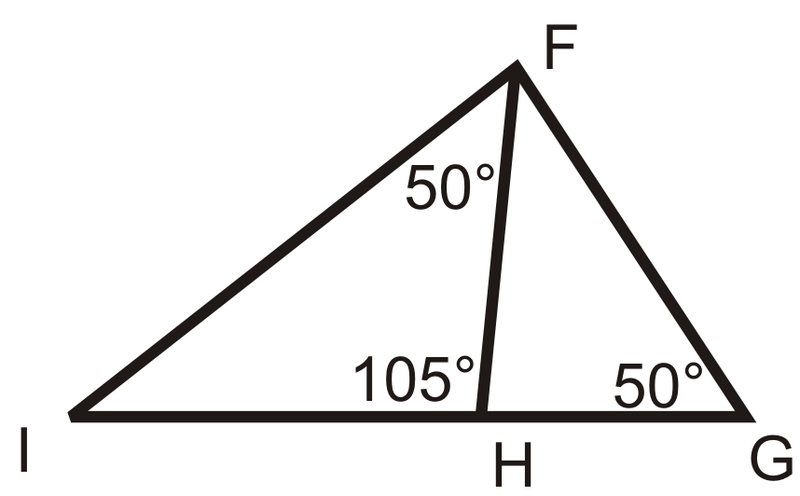
::例2Are the triangles similar? If so, write a similarity statement.
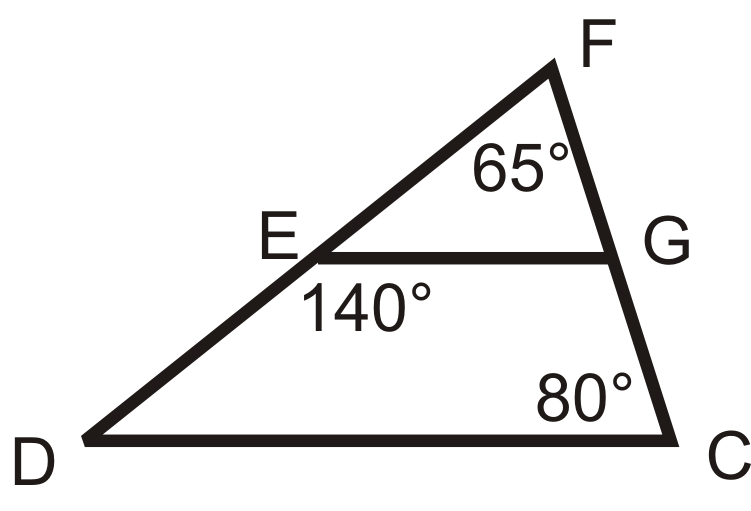
::三角形相似吗 ? 如果是, 请写一个相似语句 。By the reflexive property, ∠ H ≅ ∠ H . Because the horizontal lines are parallel , ∠ L ≅ ∠ K ( corresponding angles). So yes, there is a pair of similar triangles. H L I ∼ H K J .
::依反向属性, HHH。 因为水平线是平行的, LK (对角角度) 。 所以是的, 有一对相似的三角形。 HLIHKJ 。Example 3
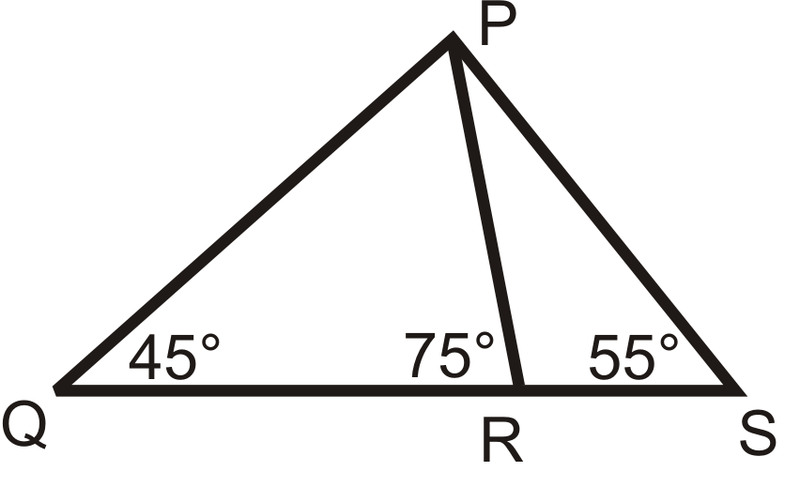
::例3Determine if the following two triangles are similar. If so, write the similarity statement.
::确定以下两个三角形是否相似。 如果是,请写入相似语句。Compare the angles to see if we can use the AA Similarity Postulate. Using the Triangle Sum Theorem , m ∠ G = 48 ∘ and m ∠ M = 30 ∘ So, ∠ F ≅ ∠ M , ∠ E ≅ ∠ L and ∠ G ≅ ∠ N and the triangles are similar. △ F E G ∼ △ M L N .
::比较角度以查看我们是否可以使用 AA 相似性假设 。 使用三角理论, mG= 48 和 mM= 30, 所以, FM, EL 和 GN 以及三角是相似的 。 @ ffeGMLN 。Example 4
::例4Determine if the following two triangles are similar. If so, write the similarity statement.
::确定以下两个三角形是否相似。 如果是,请写入相似语句。Compare the angles to see if we can use the AA Similarity Postulate. Using the Triangle Sum Theorem, m ∠ C = 39 ∘ and m ∠ F = 59 ∘ . m ∠ C ≠ m ∠ F , So △ A B C and △ D E F are not similar.
::比较角度以查看我们是否可以使用 AA 相似性假设。 使用三角理论, mC=39 和 mF=59 . mCmF, 所以 ABC 和 DEF 并不相似 。Example 5
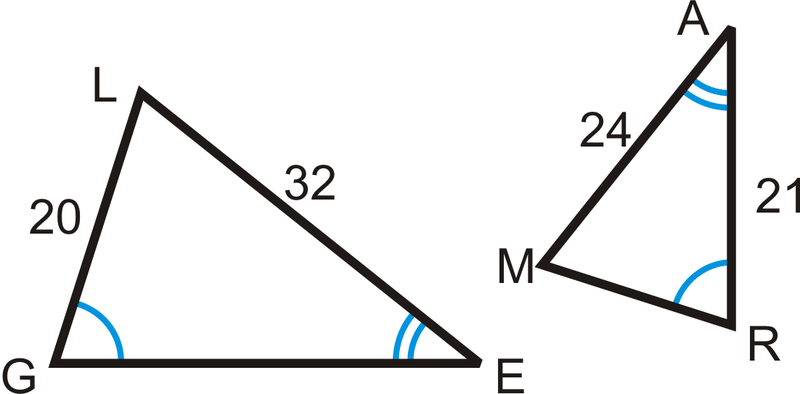
::例5△ L E G ∼ △ M A R by AA. Find G E and M R .
::AA. 找到GE和MR. 吉列尔莫·卡拉格(签名)Set up a proportion to find the missing sides.
::设定一个比例 寻找失踪的两面。24 32 = M R 20 24 32 = 21 G E 480 = 32 M R 24 G E = 672 15 = M R G E = 28
::2432=MR20 2432=21 GEGE480=32 MR24GE=67215=MRGE=28When two triangles are similar, the corresponding sides are proportional. But, what are the corresponding sides? Using the triangles from this example, we see how the sides line up in the diagram to the right.
::当两个三角形相似时, 对应的两边是比例的。 但是, 对应的两边是什么 ? 使用这个例子的三角形, 我们可以看到在图表中的两边是如何向右排列的 。Review
::回顾Use the diagram to complete each statement.
::使用图表完成每个语句 。-
△
S
A
M
∼
△
______
::萨马 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ -
S
A
?
=
S
M
?
=
?
R
I
::SA? SA? SA? SA? SA? SA? =SM? -
S
M
= ______
::SM = □ = □ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = -
T
R
= ______
::TR=___________________________________________________________________________________________________________________________________________________________________________________________ - 9 ? = ? 8
Answer questions 6-9 about trapezoid A B C D .
::回答问题6 -9 有关ABCD类甲状腺素。-
Name two similar triangles. How do you know they are similar?
::列出两个相似的三角形。 你怎么知道它们相似? -
Write a true proportion.
::写一个真正的比例。 -
If
A
B
=
10
,
A
E
=
7
,
and
D
C
=
22
, find
A
C
. Be careful!
::如果AB=10,AE=7,和DC=22, 找到AC。 要小心!
Use the triangles to the left for questions 10-14.
::问题10-14使用左侧的三角形。A B = 20 , D E = 15 , and B C = k .
::AB=20,DE=15和BC=k。-
Are the two triangles similar? How do you know?
::两个三角形相似吗? -
Write an expression for
F
E
in terms of
k
.
::以 k. 写入 FE 的表达式 。 -
If
F
E
=
12
,
, what is
k
?
::如果FE=12,什么是K? -
Fill in the blanks: If an acute angle of a _______ triangle is congruent to an acute angle in another ________ triangle, then the two triangles are _______.
::填入空格:如果 三角形的急性角与 三角形的急性角相容,则两个三角形为 。 -
Writing
How do congruent triangles and similar triangles differ? How are they the same?
::写入一致三角形和类似三角形如何不同?它们如何相同?
Are the following triangles similar? If so, write a similarity statement.
::下列三角形相似吗 ? 如果是, 请写一个相似语句 。Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。Resources
::资源 -
△
S
A
M
∼
△
______