Course: 2.3 六种三角函数和弧度

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 六三角函数和弧度

Collapse Expand
六三角函数和弧度
While working in your math class one day, you are given a sheet of values in radians and asked to find the various trigonometric functions of them, such as sine, cosine, and tangent. The first question asks you to find the $\begin{aligned} \sin \frac{π}{6} \end{aligned}$ . You are about to start converting the measurements in radians into degrees when you wonder if it might be possible to just take the values of the functions directly.
::在数学课上工作的一天,您将得到一份以弧度表示的数值表,并被要求找到其中的各种三角函数,如正弦、正弦、正弦和正弦。第一个问题要求您找到罪恶 6。当您怀疑能否直接将函数的值取下来时,您即将开始将弧度的测量值转换为度。

Do you think this is possible? As it turns out, it is indeed possible to apply trig functions to measurements in radians. Here you'll learn to do just that.
::您认为这有可能吗? 事实证明, 将三角函数应用到弧度的测量中是有可能的。在这里您将学会这样做。

Trigonometric Functions and Radians
::三角函数和弧度

Even though you are used to performing the trig functions on degrees, they still will work on radians. The only difference is the way the problem looks. If you see $\begin{aligned} \sin \frac{π}{6} \end{aligned}$ , that is still $\begin{aligned} \sin 30^{\circ} \end{aligned}$ and the answer is still $\begin{aligned} \frac{1}{2} \end{aligned}$ .
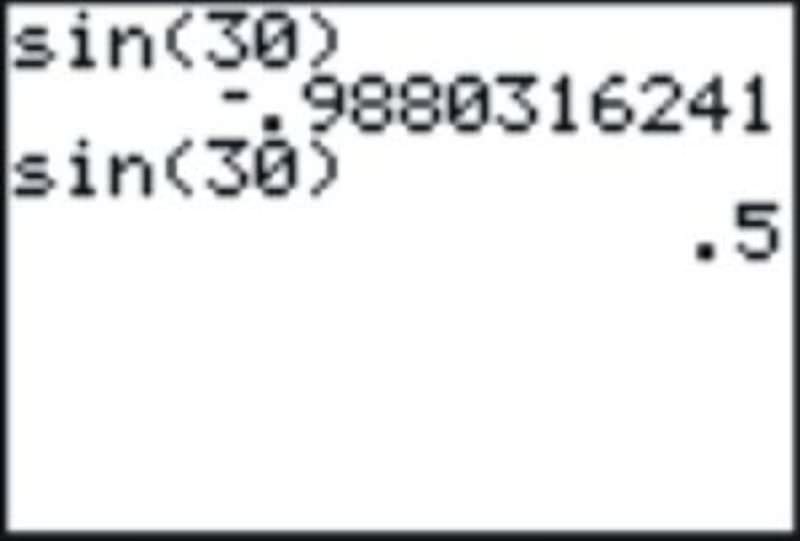
::即使你习惯在度上执行三角函数, 它们仍然会工作于弧度。唯一的区别是问题的外观。如果你看到罪6, 那仍然是罪30, 答案还是12。

Most scientific and graphing calculators have a MODE setting that will allow you to either convert between the two, or to find approximations for trig functions using either measure. It is important that if you are using your calculator to estimate a trig function that you know which mode you are using. Look at the following screen:
::大多数科学和图形化计算器都有一个 MODE 设置, 允许您在两个函数之间转换, 或使用任一测量方法为三角函数找到近似值。重要的是, 如果您正在使用计算器来估计您知道使用哪种模式的三角函数。请查看以下屏幕 :

If you entered this expecting to find the sine of 30 degrees you would realize that something is wrong because the answer should be $\begin{aligned} \frac{1}{2} \end{aligned}$ . In fact, as you may have suspected, the calculator is interpreting this as 30 radians . In this case, changing the mode to degrees and recalculating will give the expected result.
::如果您输入此期望以找到 30 度的正弦值, 您就会意识到某事是错的, 因为答案应该是 12 。事实上, 正如您可能怀疑的那样, 计算器正在将它解读为 30 度。在这种情况下, 将模式修改为度, 重新计算将会得出预期的结果。

Scientific calculators will usually have a 3-letter display that shows either DEG or RAD to tell you which mode the calculator is in.
::科学计算器通常会有一个三字母显示,显示 DEG 或 RAD 来告诉您计算器在哪个模式。

Let's take a look at a few example problems.
::让我们来看一下几个例子问题。

1. Find $\begin{aligned} \tan \frac{3 π}{4} \end{aligned}$ .
::1. 寻找tan34。

If needed, convert $\begin{aligned} \frac{3 π}{4} \end{aligned}$ to degrees. Doing this, we find that it is $\begin{aligned} 135^{\circ} \end{aligned}$ . So, this is $\begin{aligned} \tan 135^{\circ} \end{aligned}$ , which is -1.
::需要时, 将 34 转换为度。这样做时, 我们发现是 135。所以, 这是 tan 135, 也就是 - 1 。

2. Find the value of $\begin{aligned} \cos \frac{11 π}{6} \end{aligned}$ .
::2. 查找 COS116 的值。

If needed, convert $\begin{aligned} \frac{11 π}{6} \end{aligned}$ to degrees. Doing this, we find that it is $\begin{aligned} 330^{\circ} \end{aligned}$ . So, this is $\begin{aligned} \cos 330^{\circ} \end{aligned}$ , which is $\begin{aligned} \frac{\sqrt{3}}{2} \end{aligned}$ .
::需要时, 将 116 转换为度。这样做时, 我们发现是 330 。所以, 这是 cos330 32 。

3. Convert 1 radian to degree measure.
::3. 将1弧度转换为度量。

Many students get so used to using $\begin{aligned} π \end{aligned}$ in that they incorrectly think that 1 radian means $\begin{aligned} 1 π \end{aligned}$ radians. While it is more convenient and common to express radian measure in terms of $\begin{aligned} π \end{aligned}$ , don’t lose sight of the fact that $\begin{aligned} π \end{aligned}$ radians is a number. It specifies an angle created by a rotation of approximately 3.14 radius lengths. So 1 radian is a rotation created by an arc that is only a single radius in length.
::许多学生都习惯于使用 ,因为他们错误地认为 1 弧度代表 1 弧度。虽然用表示表示弧度的表示更加方便和常见, 但不要忽略弧度是一个数字的事实。它指定了一个由大约 3.14 半径长度的旋转所创造的角。因此 1 弧是一个弧的旋转, 弧的长度只有一个半径。

$\begin{aligned} radians \times \frac{180}{π} = degrees \end{aligned}$

::弧度x180 度

So 1 radian would be $\begin{aligned} \frac{180}{π} \end{aligned}$ degrees. Using any scientific or graphing calculator will give a reasonable approximation for this degree measure, approximately $\begin{aligned} {57.3}^{\circ} \end{aligned}$ .
::1 弧度为 180 °。使用任何科学或图形计算器可以给出这一度测量的合理近似值, 大约57.3 ° 。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find $\begin{aligned} \sin \frac{π}{6} \end{aligned}$ .
::早些时候,你被要求找到罪6。

As you have learned in this section, the $\begin{aligned} \sin \frac{π}{6} \end{aligned}$ is the same as $\begin{aligned} \sin 30^{\circ} \end{aligned}$ , which equals $\begin{aligned} \frac{1}{2} \end{aligned}$ . You could find this either by converting $\begin{aligned} \frac{π}{6} \end{aligned}$ to degrees, or by using your calculator with angles entered in radians.
::正如你们在本节中所学到的,罪与罪与罪相同,等于12, 可以通过将 6 转换为度,或者通过使用以弧度输入角度的计算器找到这一点。

Example 2
::例2

Using a calculator, find the approximate degree measure (to the nearest tenth) of the angle expressed in radians:
::使用计算器,找到以弧度表示角的大概度量(至最近的十分):

$\begin{aligned} \frac{6 π}{7} \end{aligned}$

$\begin{aligned} {154.3}^{\circ} \end{aligned}$

Example 3
::例3

Using a calculator, find the approximate degree measure (to the nearest tenth) of the angle expressed in radians:
::使用计算器,找到以弧度表示角的大概度量(至最近的十分):

$\begin{aligned} \frac{20 π}{11} \end{aligned}$

$\begin{aligned} {327.3}^{\circ} \end{aligned}$

Example 4
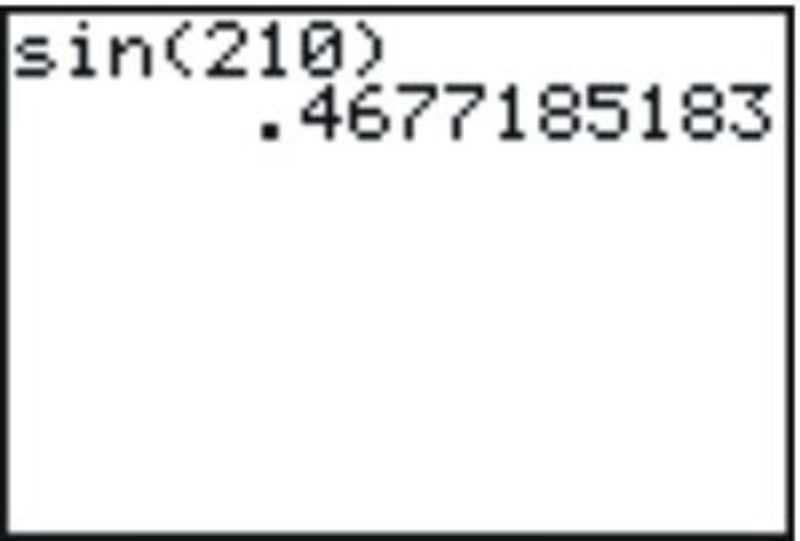
::例4

Gina wanted to calculate the $\begin{aligned} \sin 210^{\circ} \end{aligned}$ and got the following answer on her calculator:
::吉娜想计算罪210 并在计算器上得到以下答案:

Fortunately, Kylie saw her answer and told her that it was obviously incorrect.
::幸运的是,凯莉看到了她的答复,并告诉她,这显然是不正确的。

Write the correct answer, in simplest radical form.
::写正确的答案, 以最简单的激进形式。

Explain what she did wrong.
::解释一下她做错了什么

The correct answer is $\begin{aligned} - \frac{1}{2} \end{aligned}$ . Her calculator was is the wrong mode and she calculated the sine of 210 radians .
::正确的答案是- 12。她的计算器是错误的, 她计算了210弧度的正弦值。

Review
::回顾

Using a calculator, find the approximate degree measure (to the nearest tenth) of the angle expressed in radians.
::使用计算器,找到以弧度表示角的大概度量(至最近的十分)。

$\begin{aligned} \frac{4 π}{7} \end{aligned}$

$\begin{aligned} \frac{5 π}{6} \end{aligned}$

$\begin{aligned} \frac{8 π}{11} \end{aligned}$

$\begin{aligned} \frac{5 π}{3} \end{aligned}$

$\begin{aligned} \frac{8 π}{3} \end{aligned}$

$\begin{aligned} \frac{7 π}{4} \end{aligned}$

$\begin{aligned} \frac{12 π}{5} \end{aligned}$

Find the value of each using your calculator.
::使用您的计算器查找每个计算器的值。

$\begin{aligned} \sin \frac{3 π}{2} \end{aligned}$
::性别 32

$\begin{aligned} \cos \frac{π}{2} \end{aligned}$
::COs @% 2

$\begin{aligned} \tan \frac{π}{6} \end{aligned}$
::茶色 6

$\begin{aligned} \sin \frac{5 π}{6} \end{aligned}$
::56 56

$\begin{aligned} \tan \frac{4 π}{3} \end{aligned}$
::茶 43

$\begin{aligned} \cot \frac{7 π}{3} \end{aligned}$
::二氧化碳 73

$\begin{aligned} \sec \frac{11 π}{6} \end{aligned}$
::秒116

Do you think radians will always be written in terms of $\begin{aligned} π \end{aligned}$ ? Is it possible to have, for example, exactly 2 radians?
::你认为弧度总是以为单位写成吗?例如,能否有精确的 2 弧度 ?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

六三角函数和弧度

Trigonometric Functions and Radians ::三角函数和弧度

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Trigonometric Functions and Radians
::三角函数和弧度

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)