2.4 弧度的旋转

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 弧度变换

  Collapse Expand

  弧度变换

  播放段落

  In your math class one morning you finish a quiz early. While you are waiting, you watch the clock as it ticks off five minutes. The time on the clock reads 9:00. Your recent lessons have taught you that one way to measure the position of something on a circle is to use an angle. Suddenly it occurs to you that this can be applied to clocks. Can you determine the angle between the two hands of the clock?
  ::在数学课上,您在某天早上完成一个测试。 当您在等待的时候, 您可以在5分钟后看时钟。 时钟时间是9: 00 。 您最近的课程教导您, 测量圆圈上某东西位置的一种方法就是使用角度。 突然间, 您发现这个可以应用到时钟上。 您能确定时钟两只手之间的角吗 ?

  播放段落

  Rotations in Radians
  ::弧度变换

  播放段落

  A lot of interesting information about rotations and how to measure them can come from looking at clocks. We are so familiar with clocks in our daily lives that we don't often stop to think about these little devices, with hands continually rotating. Let's take a few minutes in this lesson for a closer look at these examples of rotational motion.
  ::有关旋转和如何测量它们的许多有趣的信息可以来自对钟的观察。我们非常熟悉我们日常生活中的钟,因此我们通常不会停下来思考这些小装置,手不断旋转。让我们用几分钟的时间来仔细研究这些旋转运动的例子。

  播放段落

  For the following problems, let's express in radians
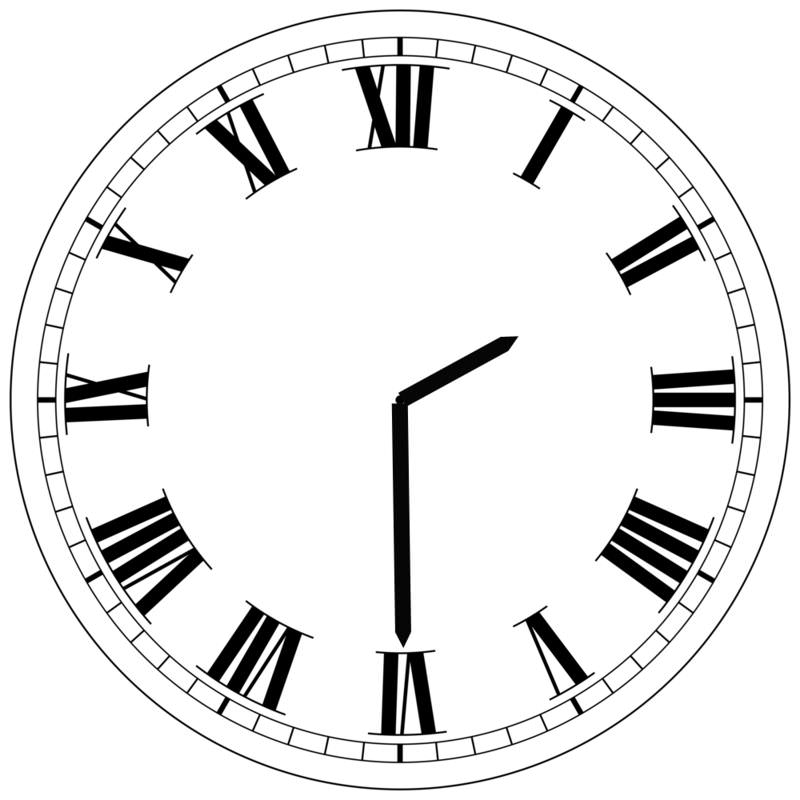
  ::对于以下的问题,让我们用弧度表示

  播放段落

  1. The hands of a clock show 11:20. Express the obtuse angle formed by the hour and minute hands in .
  ::1. 时钟手掌显示11:20. 表达时空和时空手掌所形成的斜角。

  播放段落

  The following diagram shows the location of the hands at the specified time.
  ::下图显示手在指定时间的位置。

  

  播放段落

  Because there are 12 increments on a clock, the angle between each hour marking on the clock is $\begin{array}{r}\frac{2\pi }{12}=\frac{\pi }{6}\end{array}$ (or $\begin{array}{r}{30}^{\circ }\end{array}$ ). So, the angle between the 12 and the 4 is $\begin{array}{r}4\times \frac{\pi }{6}=\frac{2\pi }{3}\end{array}$ (or $\begin{array}{r}{120}^{\circ }\end{array}$ ). Because the rotation from 12 to 4 is one-third of a complete rotation, it seems reasonable to assume that the hour hand is moving continuously and has therefore moved one-third of the distance between the 11 and the 12. This means that the angle between the hour hand and the 12 is two-thirds of the distance between the 11 and the 12. So, $\begin{array}{r}\frac{2}{3}\times \frac{\pi }{6}=\frac{2\pi }{18}=\frac{\pi }{9}\end{array}$ , and the total measure of the angle is therefore $\begin{array}{r}\frac{\pi }{9}+\frac{2\pi }{3}=\frac{\pi }{9}+\frac{6\pi }{9}=\frac{7\pi }{9}\end{array}$ .
  ::由于时钟有12个加分, 时钟每小时标记之间的角是 2126 (或 30)。 因此, 12与 4 之间的角是 46= 23( 或 120)。 由于12 至 4 的旋转是完全旋转的三分之一, 似乎有理由假定小时手在连续移动, 因此移动了 11 和 12 之间的距离的三分之一。 这意味着时手与 12 之间的角是 11 和 12 之间的距离的三分之二。 所以, 236= 2189 , 角度的总尺寸是 9+23 9+69= 79。

  播放段落

  2. Express in radians
  ::2. 以弧度表示

  播放段落

  The hands of a clock show 4:15. Express the acute angle formed by the hour and minute hands in radian measure.
  ::时钟的手显示 4: 15 。 以弧度表示时空和小手的急性角度 。

  

  播放段落

  Because there are 12 increments on a clock, the angle between each hour marking on the clock is $\begin{array}{r}\frac{2\pi }{12}=\frac{\pi }{6}\end{array}$ (or $\begin{array}{r}{30}^{\circ }\end{array}$ ). So, the angle between the 3 (which is where the minute hand is located when it is 15 minutes after the hour) and the 4 is $\begin{array}{r}\frac{\pi }{6}\end{array}$ (or $\begin{array}{r}{30}^{\circ }\end{array}$ ). Further, since the minute hand has moved one quarter of the way around the hour, we can infer that the hour hand has moved one quarter of the way between four and five, which is $\begin{array}{r}\frac{1}{4}\times \frac{\pi }{6}=\frac{\pi }{24}\end{array}$ . Adding these numbers gives: $\begin{array}{r}\frac{\pi }{6}+\frac{\pi }{24}=\frac{4\pi }{24}+\frac{\pi }{24}=\frac{5\pi }{24}\end{array}$ .
  ::由于时钟有12个加分, 时钟每小时标记之间的角是 2126 (或 30)。 因此, 时钟3( 时钟后15分钟是分钟手的位置) 与 4( 时钟后15分钟) 之间的角是 6 (或 30) 。 此外, 由于时钟每小时移动四分之一, 我们可以推断, 时钟手移动了四分之一 4到 5, 即 14624 。 加上这些数字, 则显示: 624= 424= 524 。

  播放段落

  3. The hands of a clock show 2:30. Express the acute angle formed by the hour and minute hands in radian measure.
  ::3. 时钟手掌显示2:30,用弧度表示时空和小手的急角。

  

  播放段落

  Because there are 12 increments on a clock, the angle between each hour marking on the clock is $\begin{array}{r}\frac{2\pi }{12}=\frac{\pi }{6}\end{array}$ (or $\begin{array}{r}{30}^{\circ }\end{array}$ ). Since the hour hand would actually be partway between the 2 and the 3 at 2:30, start by determining the angular distance between the 3 and the 6, then you can add the additional portion between the 2 and the 3:
  ::由于时钟上加了12个加分, 时钟上每小时标记之间的角是 2126 (或 30 ) 。 由于小时手在 2 : 30时实际上是 2 : 2 : 3 : 3 : 3 : 6 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 2 : : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : 3 : : : 2 : : 2 : : 2 : 2 : : : 3 3 : 3 : : : : : 30 3 3 : 3 : 3 : : 3 3 3 : 3 : : 3 3 : 3 3 : 2 : 2 : 2 : 2 : 2 : 2 : : : 2 : : : 2 : : : : 2 3 3 3 3 : : : : : : : 2 : : : : : : 2 : : 2 : : : : : : : : : 2 : 2 : 2 : 2 : : : : : : : : : : : : : 2 : 2 : 2 : : 2 : 2 3 3 3 3 3 : : : : : : 2 3 : : 2 : 2 : 2 : 2 : 2 : : 2 : 2 : 2 : 2 : 2

  播放段落
  • The angle between the 3 and the 6 (which is where the minute hand is at 30 minutes after the hour) is $\begin{array}{r}3\times \frac{\pi }{6}=\frac{3\pi }{6}=\frac{\pi }{2}\end{array}$ (or $\begin{array}{r}{90}^{\circ }\end{array}$ ).
    ::3 和 6 之间的角度(即分钟手在时后30分钟)是 3 6= 3 6 Q 2(或 90 Q) 。
  播放段落
  • Because the rotation from 12 to 6 is one-half of a complete rotation, it seems reasonable to assume that the hour hand is moving continuously and has therefore moved one-half of the distance between the 2 and the 3. This means that the angle between the hour hand and the 3 is one-half of the distance between the 2 and the 3. So, $\begin{array}{r}\frac{1}{2}\times \frac{\pi }{6}=\frac{\pi }{12}.\end{array}$
    ::因为12到6的旋转是完全旋转的一半,所以似乎有理由假定小时手在不断移动,因此移动了2到3之间的距离的一半,这意味着小时手与3之间的角是2到3之间的距离的一半,所以是12612。
  播放段落
  • The total measure of the angle is therefore $\begin{array}{r}\frac{\pi }{12}+\frac{\pi }{2}=\frac{\pi }{12}+\frac{6\pi }{12}=\frac{7\pi }{12}\end{array}$ .
    ::因此,角度的总度量是... 122212+612=712。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked if you can determine the angle between the two hands of a clock. 
  ::早些时候,有人问您能否确定时钟两只手之间的角。

  播放段落

  Since you now know that the angle between the hours on a clock is $\begin{array}{r}\frac{\pi }{6}={30}^{\circ }\end{array}$ , you can use this information to construct an answer. There are three hours between the 9 and the 12 on a clock, so the answer is:
  ::既然你现在知道时钟时数之间的角度是 '6=30\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"6\\\\\\\\\\\\\\"6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  $\begin{array}{r}3\times \frac{\pi }{6}=\frac{3\pi }{6}=\frac{\pi }{2}={90}^{\circ }\end{array}$

  播放段落

  So there are $\begin{array}{r}{90}^{\circ }\end{array}$ degrees between the 9 and 12 on the clock.
  ::所以在9点到12点之间有90度

  播放段落

  The following image shows a 24-hour clock.
  ::以下图像显示24小时24小时。

  

  播放段落

  Example 2
  ::例2

  播放段落

  What is the angle between each number of the clock expressed in exact radian measure in terms of $\begin{array}{r}\pi \end{array}$ ?
  ::以精确弧度度量表示的每个钟数之间的角度是什么?

  播放段落

  Since there are $\begin{array}{r}2\pi \end{array}$ radians in a circle, and there are 24 separate increments, the answer is $\begin{array}{r}\frac{2\pi }{24}=\frac{\pi }{12}\end{array}$
  ::由于圆圈里有2弧度, 并且有24个单独的递增, 答案是 22412 。

  播放段落

  Example 3
  ::例3

  播放段落

  What is the angle between each number of the clock expressed to the nearest tenth of a radian? What about in degree measure?
  ::表示为最接近十分之一弧度的时钟数之间的角是多少? 度量如何?

  播放段落

   Since there are $\begin{array}{r}2\pi \end{array}$ radians in a circle, the number of radians in each of 24 different divisions is $\begin{array}{r}\frac{2\pi }{24}\approx .3\end{array}$ . In degrees we can do the same by taking the number of degrees in a circle and dividing it by 12: $\begin{array}{r}\frac{360}{24}={15}^{\circ }\end{array}$ .
  ::由于圆内有2弧度, 24个不同的分区中每个分区的弧度数为 2243. 。 在度上, 我们可以通过在圆内取出度数, 将其除以 12: 36024=15\ 来做相同的事情 。

  播放段落

  Example 4
  ::例4

  播放段落

  Estimate the measure of the angle between the hands at the time shown to the nearest whole degree. And then in radian measure in terms of $\begin{array}{r}\pi \end{array}$ .
  ::估计显示时手与手之间的角度到最接近的整度。然后用弧度测量 。

  播放段落

  $\begin{array}{r}{20}^{\circ }\end{array}$ . Answers may vary, anything above $\begin{array}{r}{15}^{\circ }\end{array}$ and less than $\begin{array}{r}{25}^{\circ }\end{array}$ is reasonable. In radians, this is $\begin{array}{r}\frac{\pi }{9}\end{array}$ . Again, answers may vary.
  ::20。 答案可能不同, 任何高于 15 和小于 25 的答案都是合理的。 在弧度中, 这是 9 。 答案也可能不同 。

  播放段落

  Review
  ::回顾

  播放段落

  Use the clock below to help you find the angle between the hour hand and minute hand at each of the following times. Express your answer in degrees less than $\begin{array}{r}{180}^{\circ }\end{array}$ . Then express your answer in radian measure in terms of $\begin{array}{r}\pi \end{array}$ .
  ::使用下面的时钟来帮助您在接下来的每个时间找到小时手与分钟手之间的角。 以小于 180 度表示您的回答。 然后以 ° 表示您的回答, 以弧度表示 ° 表示 。

  

  1. 3:30
  2. 5:15
  3. 4:45
  4. 6:30
  5. 6:15
  6. 2:30
  7. 12:30
  8. 9:30
  9. 10:15
  10. 11:30
  11. 3:45
  12. 2:15
  13. 7:15
  播放段落
  14. How many times in 12 hours will the hour and minute hands overlap?
      ::12小时12小时的时空和小手会重叠多少次?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。