2.5弧的长度

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 弧的长度

  Collapse Expand

  弧的长度

  播放段落

  You have taken your little cousin to the amusement park for the day. While there, she decides she would like a ride on the carousel. After the ride, she excitedly bounces over to you. She is amazed that she went around, but in a way ‘‘didn't go anywhere’’, since she ended up where she started.
  ::你带小表妹去游乐园玩了一天,她决定搭顺风车,在车后,她兴奋地跳到你身边。她很惊讶她绕圈子,但从某种意义上说,她没有去任何地方,因为她从她开始的地方来到了那里。

  播放段落

  ‘‘How far did I go when I was halfway around the turn?’’, she asks.
  ::转弯时我走了多远?

  播放段落

  You know that the radius of the carousel is 7 meters. Can you tell your little cousin how far she went in one half of a turn around the ride?
  ::你知道旋转木马的半径是7米 你能告诉你的小表弟 她转半圈的车程有多远吗?

  播放段落

  Length of an Arc
  ::弧的长度

  播放段落

  The length of an arc on a circle depends on both the angle of rotation and the radius length of the circle. If you recall from the last lesson, the measure of an angle in radians is defined as the length of the arc cut off by one radius length. What if the radius is 4 cm? Then, the length of the half-circle arc would be $\begin{array}{r}\pi \end{array}$ multiplied by the radius length, or $\begin{array}{r}4\pi \end{array}$ cm in length.
  ::圆的弧长度取决于圆的旋转角度和圆的半径长度。如果您从最后一个课中记得,弧度中角的测量值被定义为弧以半径长度截断的弧长度。如果半径为 4 厘米呢? 那么半圆弧的长度会乘以 + 乘以半径长度, 或 4 cm 长度。

  

  播放段落

  This results in a formula that can be used to calculate the length of any arc.
  ::这将产生一个公式, 可用于计算任何弧的长度 。

  播放段落

  $$\begin{array}{r}s=r\theta ,\end{array}$$

  
  ::s=r,

  播放段落

  where $\begin{array}{r}s\end{array}$ is the length of the arc, $\begin{array}{r}r\end{array}$ is the radius, and $\begin{array}{r}\theta \end{array}$ is the measure of the angle in radians.
  ::s 是弧的长度, r 是半径, \ 是以弧度衡量角。

  播放段落

  Solving this equation for $\begin{array}{r}\theta \end{array}$ will give us a formula for finding the given the arc length and the radius length.
  ::解决 % 的方程将给我们一个公式, 找到给定的弧长度和半径长度 。

  播放段落

  Let's look at some problems involving arc length. 
  ::让我们来看看一些问题 涉及弧长度。

  播放段落

  1. Find the length of the arcs
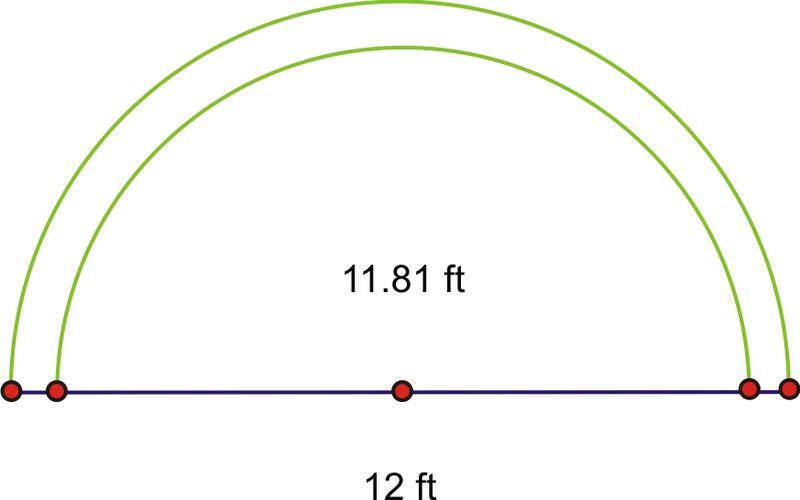
  ::1. 查找弧的长度

  播放段落

  The free-throw line on an NCAA basketball court is 12 ft wide. In international competition, it is only about 11.81 ft. How much longer is the half circle above the free-throw line on the NCAA court?
  ::NCAA篮球场的自由发射线宽12英尺,在国际竞争中,只有11.81英尺。 NCAA法院的自由发射线上方的半圈还有多久?

  

  播放段落

  Find both arc lengths.
  ::查找两个弧长度 。

  播放段落

  $$\begin{array}{rlrl}& \text{NCAA}& & \text{INTERNATIONAL}\\ & s_1=r\theta & & s_2=r\theta \\ & s_1=\frac{12}{2}(\pi )& & s_2\approx \frac{11.81}{2}(\pi )\\ & s_1=6\pi & & s_2\approx 5.905\pi \end{array}$$

  
  ::NCAINTIONs1=rQs2=rQs1=122()s211.812()s1=6Qs25.905}

  播放段落

  So the answer is approximately $\begin{array}{r}6\pi -5.905\pi \approx 0.095\pi \end{array}$
  ::所以答案大约是 65.9050.095

  

  播放段落

  This is approximately 0.3 ft, or about 3.6 inches longer.
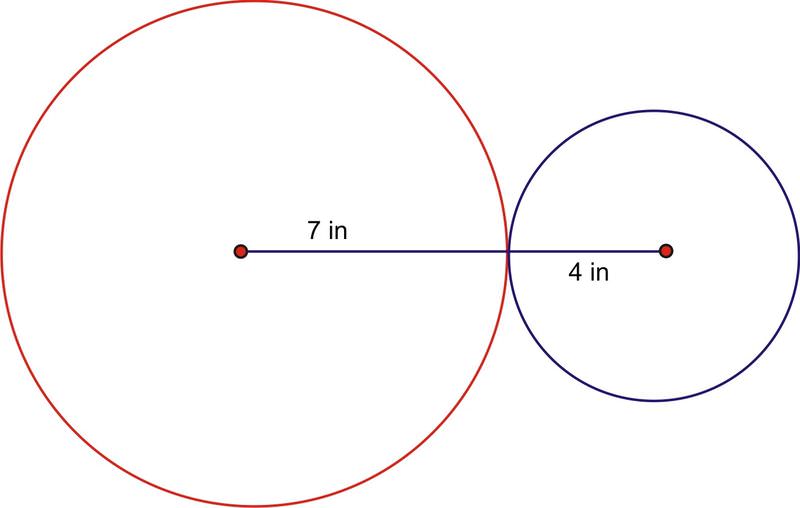
  ::大约为0.3英尺,或3.6英寸长。

  播放段落

  2. Two connected gears are rotating. The smaller gear has a radius of 4 inches and the larger gear’s radius is 7 inches. What is the angle through which the larger gear has rotated when the smaller gear has made one complete rotation?
  ::2. 两个连接的齿轮在旋转,较小的齿轮半径为4英寸,较大的齿轮半径为7英寸。

  

  播放段落

  Because the blue gear performs one complete rotation, the length of the arc traveled is:
  ::因为蓝色渔具是一个完整的旋转, 航程的弧长度是:

  播放段落

  $$\begin{array}{rl}s& =r\theta \\ s& =4\times 2\pi \end{array}$$

  
  ::s=rs=4×2

  播放段落

  So, an $\begin{array}{r}8\pi \end{array}$ arc length on the larger circle would form an angle as follows:
  ::因此,大圆上的8-弧长度将形成如下角度:

  播放段落

  $$\begin{array}{rl}\theta & =\frac{s}{r}\\ \theta & =\frac{8\pi }{7}\\ \theta & \approx 3.6\end{array}$$

  
  ::873.6

  播放段落

  So the angle is approximately 3.6 radians.
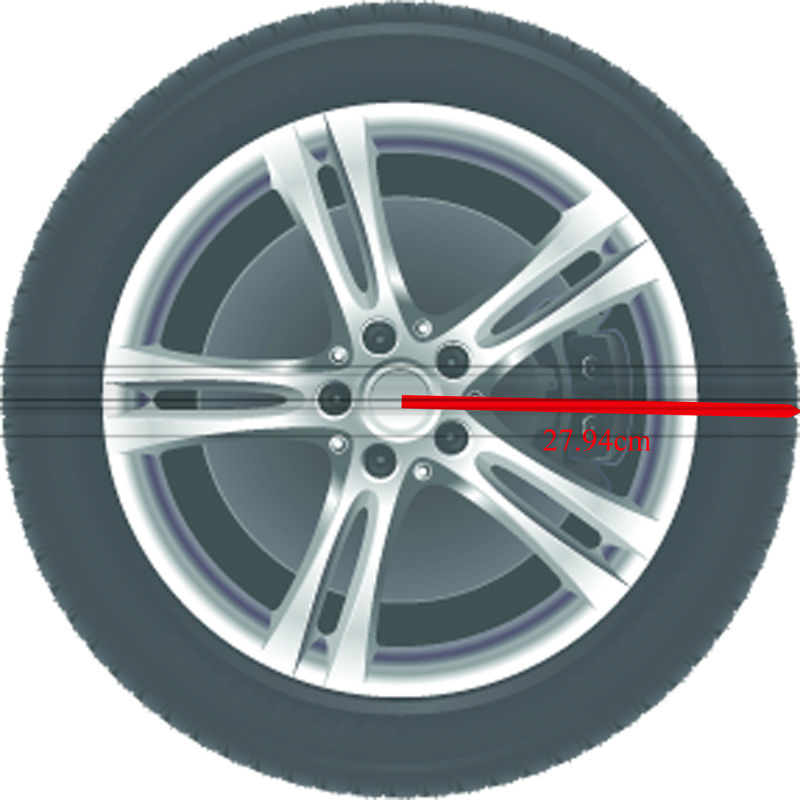
  ::角度大约是3.6弧度

  $$\begin{array}{r}3.6\times \frac{180}{\pi }\approx {206}^{\circ }\end{array}$$

  播放段落

  3. The radius of a standard car tire is 27.94 cm. How far does a car go in one revolution of the tire?
  ::3. 标准车胎半径为27.94厘米。 一辆车在一次轮胎革命中能走多远?

  

  播放段落

  Since the distance traveled by the tire is equal to the distance around the tire, we can use the circumference of the tire to answer the question.
  ::由于轮胎行驶的距离相当于轮胎周围的距离,我们可以使用轮胎的环绕来回答问题。

  播放段落

  $$\begin{array}{rl}s& =r\theta \\ s& =(27.94)(2\pi )\\ s& =175.46\end{array}$$

  
  ::s=rs=(27.94)(2)s=175.46

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked can you tell your little cousin how far she went in one half of a turn around the ride. 
  ::之前有人问过你 你能告诉你的小表弟 她转半圈的车程有多远吗?

  播放段落

  Since you now know that you can measure an arc length using $\begin{array}{r}s=r\theta \end{array}$ , you can use this to find a solution to your cousin's question. Since your cousin wants to know how far she went around when she went $\begin{array}{r}\frac{1}{2}\end{array}$ of a rotation, and the radius of the ride is 7 meters, you can calculate her arc length:
  ::既然你现在知道可以使用 s=r 来测量弧长度, 您可以用这个来找到解决你堂兄问题的办法。 由于你的堂弟想知道当她转12圈时她走多远, 车的半径是7米, 您可以计算她的弧长度 :

  播放段落

  $\begin{array}{r}s=r\theta =7\pi \approx 21.98meters\end{array}$
  ::21.98 公尺

   

  播放段落

  Example 2
  ::例2

  播放段落

  You are trying to push your car after it has broken down. Unfortunately, you aren't very strong, and so the car is just rocking back and forth instead of rolling as you push. If the radius of your car's tire is 14 inches, and the change in the tire's angle is $\begin{array}{r}\frac{\pi }{2}\end{array}$ radians, how far did the tire move?
  ::你试图在车坏了之后推车。 不幸的是,你并不很强壮,所以汽车只是来回摇晃,而不是在推车时滚动。如果车胎的半径是14英寸,轮胎角度的改变是2弧度,轮胎移动了多远?

  播放段落

  Since the distance the tire moved is equal to the length of the arc the tire rolled, you can use the equation $\begin{array}{r}s=r\theta \end{array}$ to determine how far the tire went:
  ::由于轮胎移动的距离等于轮胎滚动弧的长度,你可以使用方程式s=r确定轮胎走多远:

  播放段落

  $$\begin{array}{r}s=r\theta \\ s=(14)(\frac{\pi }{2})\\ s=7\pi \\ s\approx 21.98in\end{array}$$

  
  ::s=rs=( 14) (%2)s= 7s=21. 98in

   

  播放段落

  Example 3
  ::例3

  播放段落

  If an object with a radius of 10 cm spins so that its arc covers 54 cm, what is the change in angle of the object?
  ::如果一个半径为 10 厘米旋转的物体使其弧覆盖54 厘米,则对象角度的变化是什么?

   

  播放段落

  You can again use the equation $\begin{array}{r}s=r\theta \end{array}$ to solve this problem:
  ::您可以再次使用公式 s=r 来解决这个问题 :

  播放段落

  $$\begin{array}{r}s=r\theta \\ \theta =\frac{s}{r}=\frac{54}{10}=5.4\end{array}$$

  
  ::s=rsr=5410=5.4

  播放段落

  The disk moves 5.4 radians, which is a little less than a complete rotation, since a complete rotation is approximately 6.28 radians.
  ::磁盘移动5.4弧度,略低于完全旋转,因为完全旋转约为6.28弧度。

  播放段落

  Example 4
  ::例4

  播放段落

  If your DVD has a radius of 4.5 inches, how far does a point on the disk spin if the player turns it $\begin{array}{r}\frac{\pi }{2}\end{array}$ radians?
  ::如果您的 DVD 半径为 4.5 英寸, 如果播放器旋转 2 弧度, 磁盘旋转的点有多远 ?

  播放段落

  Using $\begin{array}{r}s=r\theta \end{array}$ ,
  ::使用 s=r,

  播放段落

  $$\begin{array}{r}s=r\theta \\ s=(4.5)(\frac{\pi }{2})\\ s=2.25\pi \approx 7.065\end{array}$$

  
  ::s=rs=(4.5)(2)s=2.257.65

  播放段落

  A point on the disk turns 7.065 inches.
  ::磁盘上的一个点翻转7.065英寸

  播放段落

  Review
  ::回顾

  播放段落

  The radius of a carousel is 8 meters. Use this information to answer questions 1-3.
  ::旋转木马的半径是8米 使用此信息回答问题1 -3

  播放段落
  1. You are half way around the carousel. How far did you travel?
     ::你绕着旋转木马绕了半个路程 你走了多远?
  播放段落
  2. You are all the way around the carousel. How far did you travel?
     ::你绕着旋转木马到处跑 你跑到哪里去了?
  播放段落
  3. You have now traveled all the way around the carousel twice. How far did you travel?
     ::你们已经绕着旋转木马绕了两次路了 你们跑到哪里去了?

  播放段落

  A pizza has a radius of 10in. Use this information to answer questions 4-6.
  ::披萨半径为10英寸 用这个信息回答问题4 -6

  播放段落
  4. A slice is removed. The length of the crust of the missing slice is 3in. What is the central angle of the missing slice?
     ::切片被切除。 遗漏切片的地壳长度是 3 英寸。 遗漏切片的中心角度是什么 ?
  播放段落
  5. You eat three pieces with a central angle of $\begin{array}{r}\frac{4\pi }{5}\end{array}$ . What is the length of the crust you ate?
     ::你吃三片,中央角度是4 5,你吃地壳的长度是多少?
  播放段落
  6. A large pizza has a radius of 12in. What is the length of the crust of half of the large pizza?
     ::大披萨的半径是12英寸 大披萨一半的地壳长度是多少?

  播放段落

  The diameter of a tire is 35in. Use this information to answer questions 7-10.
  ::轮胎直径为35英寸,使用这些信息回答问题7-10。

  播放段落
  7. What is the length around the whole tire?
     ::整个轮胎的长度是多少?
  播放段落
  8. The tire travels one mile (5280 ft). How many revolutions did the tire make?
     ::轮胎行驶1英里(5280英尺)。轮胎进行了多少次革命?
  播放段落
  9. You roll the tire so it rotates $\begin{array}{r}7\pi \end{array}$ radians. How far did it move?
     ::你把轮胎卷起来,然后它旋转7弧度 它移动了多远?
  播放段落
  10. The tire travels half a mile. How many radians did the tire rotate?
      ::轮胎转动了多少弧度?

  播放段落

  Consider a standard 12 hour clock like the one below with a radius of 5 inches. Use this to answer questions 11-15.
  ::考虑一个标准的12小时钟, 和下面的一样, 半径为 5 英寸。 用它回答问题 11-15 。

  

  播放段落
  11. What is the length of the arc between the 3 and the 7?
      ::3和7之间的弧长度是多少?
  播放段落
  12. What is the length of the arc between the 3 and the 2?
      ::3和2之间的弧长度是多少?
  播放段落
  13. It is 12:30. What is the length of the arc between the minute and hour hands?
      ::现在是12: 30 分钟与小时之间方弧的长度是多少?
  播放段落
  14. It is 7:20. What is the length of the arc between the minute and hour hands?
      ::现在是7: 20。 分钟与小时之间的弧长度是多少?
  播放段落
  15. It is 1:25. What is the length of the arc between the minute and hour hands?
      ::现在是1: 25 。 分钟与小时手之间的弧长度是多少?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。