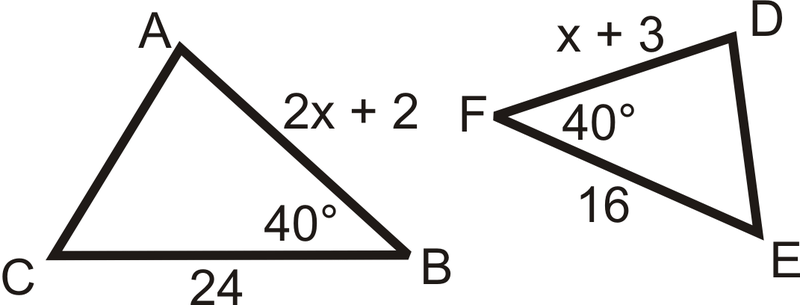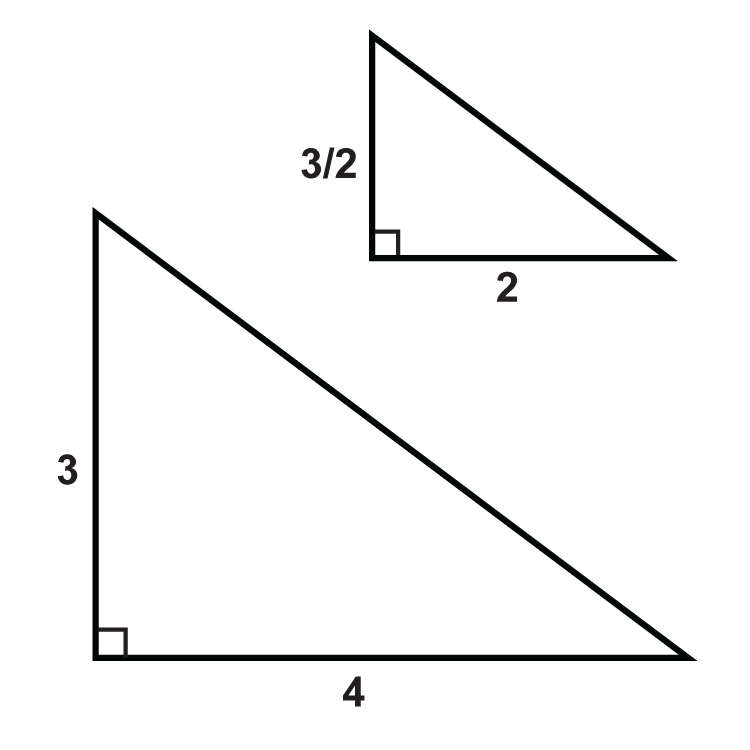7.7 SAS 相似性

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section SAS SAS 相似性

  Collapse Expand

  SAS SAS 相似性

  播放段落

  SAS Similarity Theorem
  ::SAS 相似理论

  播放段落

  By definition, two triangles are similar if all their are congruent and their corresponding sides are proportional. It is not necessary to check all angles and sides in order to tell if two triangles are similar. In fact, if you know only that two pairs of sides are proportional and their included angles are congruent, that is enough information to know that the triangles are similar. This is called the SAS Similarity Theorem .
  ::按定义,如果两个三角形都一致,而相应的两边是成比例的,则两个三角形是相似的。没有必要检查所有角度和两边来判断两个三角形是否相似。事实上,如果你只知道两对边是成比例的,而且它们包含的角是相匹配的,那么,这足以说明三角形是相似的。这被称为SAS相似性定理。

  播放段落

  SAS Similarity Theorem: If two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar.
  ::SAS 相似性理论:如果一个三角的两边与另一个三角的两边成正比,而两者中包括的角是相同的,那么这两个三角是相似的。

  播放段落

  If $\begin{align*}\frac{AB}{XY} = \frac{AC}{XZ}\end{align*}$ and $\begin{align*}\angle A \cong \angle X\end{align*}$ , then $\begin{align*}\triangle ABC \sim \triangle XYZ\end{align*}$ .
  ::如果ABXY=ACXZ和ZAX,那么AABC=XYZ。

  播放段落

  What if you were given a pair of triangles, the lengths of two of their sides, and the measure of the angle between those two sides? How could you use this information to determine if the two triangles are similar?
  ::如果你们获得一对三角形、两边的长度和两边角的度量呢?你们如何利用这一信息来确定这两个三角形是否相似?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Determine if the following triangles are similar. If so, write the similarity theorem and statement.
  ::确定以下三角形是否相似。 如果是, 请写入相似的定理和语句 。

  

  播放段落

  We can see that $\begin{align*}\angle{B} \cong \angle{F}\end{align*}$ and these are both included angles. We just have to check that the sides around the angles are proportional.
  ::我们可以看到这些都包含角度。我们只需要检查角度周围的侧面是比例的。

  播放段落

  $\begin{align*}\frac{AB}{DF}=\frac{12}{8}=\frac{3}{2}\end{align*}$
  ::ABDF=128=32

  播放段落

  $\begin{align*}\frac{BC}{FE}=\frac{24}{16}=\frac{3}{2}\end{align*}$
  ::BCFE=2416=32

  播放段落

  Since the ratios are the same $\begin{align*}\triangle ABC \sim \triangle DFE \end{align*}$ by the SAS Similarity Theorem.
  ::由于该比率与SAS相似理论中的比率相同,所以该比率与SAS相似理论相同。

  播放段落

  Example 2
  ::例2

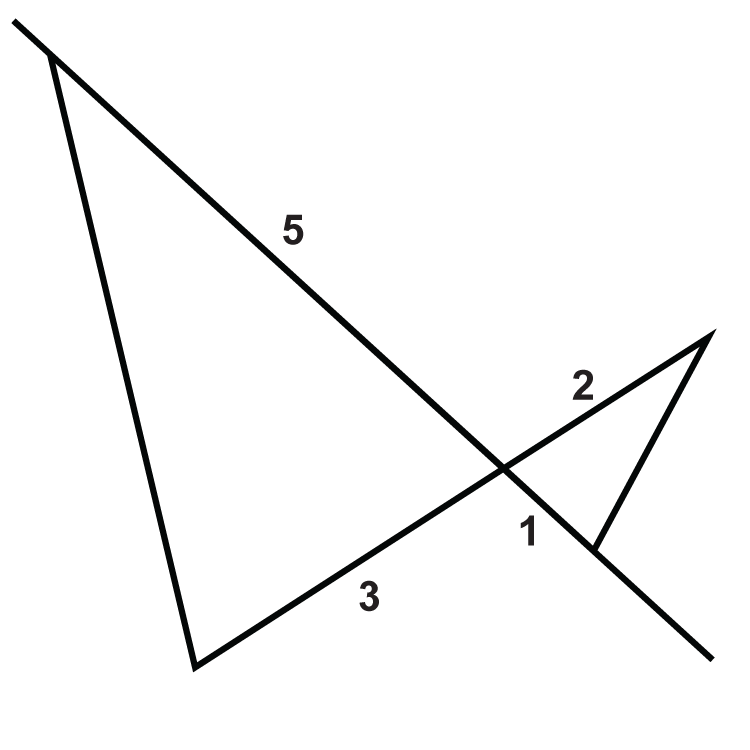
  播放段落

  Determine if the following triangles are similar. If so, write the similarity theorem and statement.
  ::确定以下三角形是否相似。 如果是, 请写入相似的定理和语句 。

  

  播放段落

  The triangles are not similar because the angle is not the included angle for both triangles.
  ::三角形不相似, 因为角不是两个三角形的包含角 。

  播放段落

  Example 3
  ::例3

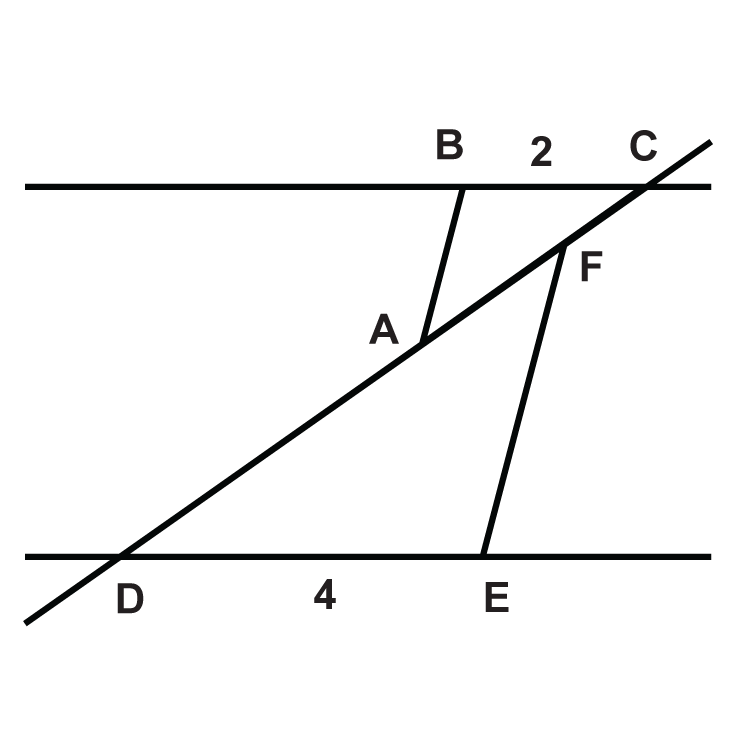
  播放段落

  Are the two triangles similar? How do you know?
  ::两个三角形相似吗?

  

  播放段落

  We know that $\begin{align*}\angle B \cong \angle Z\end{align*}$ because they are both right angles and $\begin{align*}\frac{10}{15} = \frac{24}{36}\end{align*}$ . So, $\begin{align*}\frac{AB}{XZ} = \frac{BC}{ZY}\end{align*}$ and $\begin{align*}\triangle ABC \sim \triangle XZY\end{align*}$ by .
  ::因为他们是右角度 和1015=2436。所以,ABXBZY 和 ABCXZY。

  播放段落

  Example 4
  ::例4

  播放段落

  Are there any similar triangles in the figure? How do you know?
  ::图表中是否有相似的三角形? 你怎么知道?

  

  播放段落

  $\begin{align*}\angle A\end{align*}$ is shared by $\begin{align*}\triangle EAB\end{align*}$ and $\begin{align*}\triangle DAC\end{align*}$ , so it is congruent to itself. Let’s see if $\begin{align*}\frac{AE}{AD} = \frac{AB}{AC}\end{align*}$ .
  ::“A”与“EAB”和“DAC”相同,因此彼此一致。让我们看看是否AEAD=ABAC。

  播放段落

  $$\begin{align*}\frac{9}{9+3} &= \frac{12}{12+5}\\ \frac{9}{12} &= \frac{3}{4} \neq \frac{12}{17} && \text {The two triangles are} \ not \ \text{similar.}\end{align*}$$
  ::99+3=1212+5912=341217 两个三角形不相似

  播放段落

  Example 5
  ::例5

  播放段落

  From Example 4, what should $\begin{align*}BC\end{align*}$ equal for $\begin{align*}\triangle EAB \sim \triangle DAC\end{align*}$ ?
  ::从例4来看,《巴塞尔公约》与“EAB”和“发援会”的“BC”等值是多少?

  播放段落

  The proportion we ended up with was $\begin{align*}\frac{9}{12} = \frac{3}{4} \neq \frac{12}{17}\end{align*}$ . $\begin{align*}AC\end{align*}$ needs to equal 16, so that $\begin{align*}\frac{12}{16} = \frac{3}{4}\end{align*}$ . $\begin{align*}AC = AB + BC\end{align*}$ and $\begin{align*}16 = 12 + BC\end{align*}$ . $\begin{align*}BC\end{align*}$ should equal 4.
  ::我们最后得出的比例是912=341117。 丙烷需要等于16, 因此, 1216=34。 丙烷=AB+BC, 16=12+BC。 BC应该等于4。 BC应该等于4。

  播放段落

  Review
  ::回顾

  播放段落

  Fill in the blanks.
  ::填满空白。

  播放段落
  1. If two sides in one triangle are _________________ to two sides in another and the ________________ angles are _________________, then the triangles are ______________.
     ::如果一个三角形的两边是++++和另一边的两边, 角度是++++, 那么三角形是 +++++ 。

  播放段落

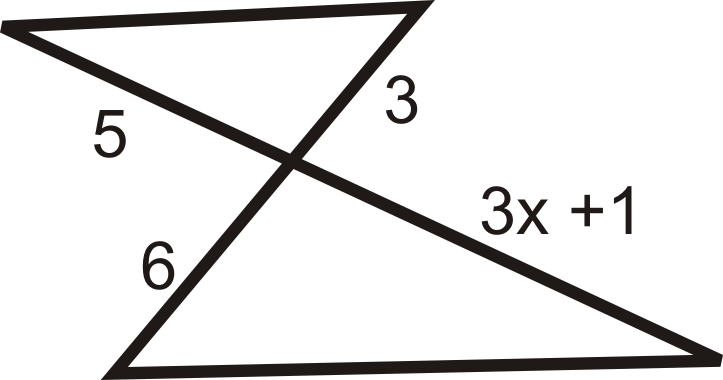
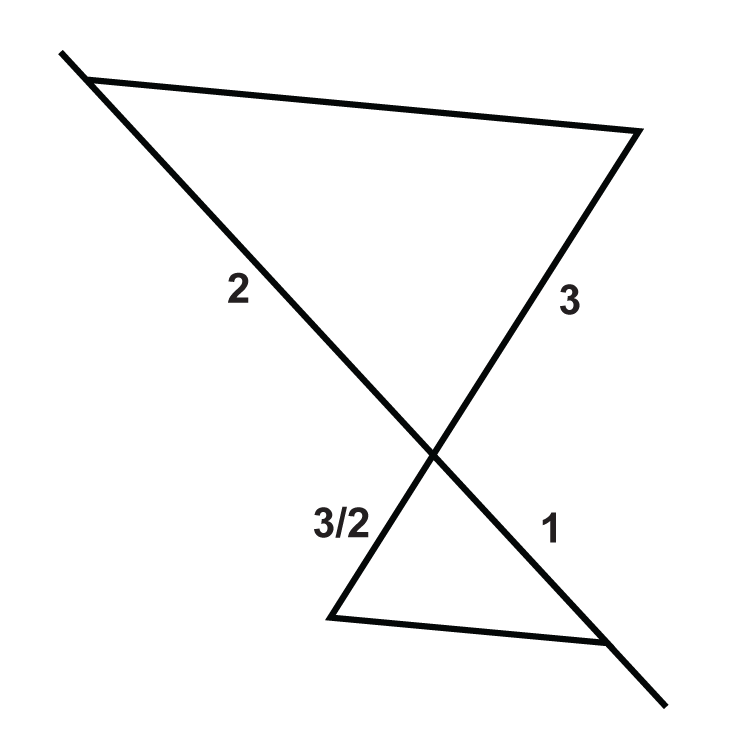
  Determine if the following triangles are similar. If so, write the similarity theorem and statement.
  ::确定以下三角形是否相似。 如果是, 请写入相似的定理和语句 。

  2. 

  播放段落

  Find the value of the missing variable(s) that makes the two triangles similar.
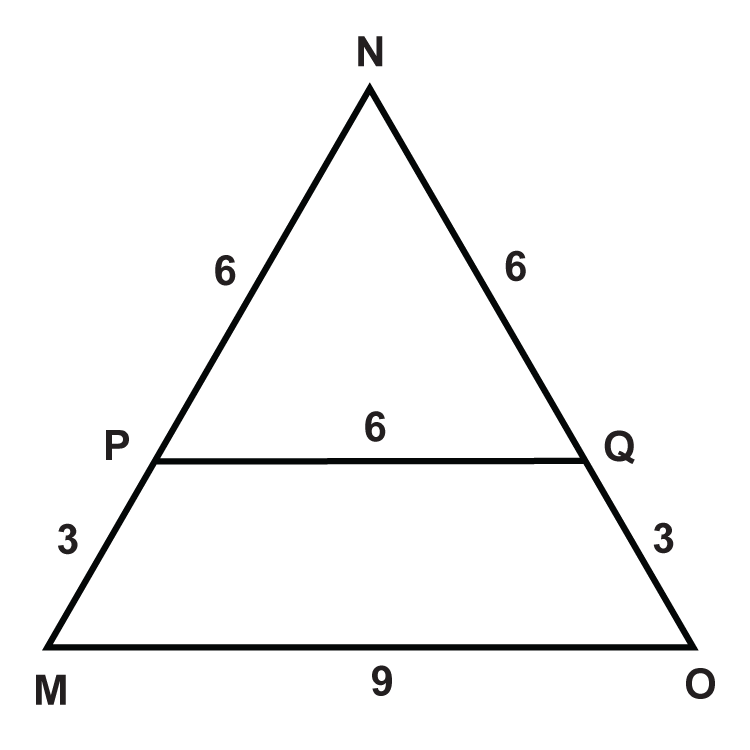
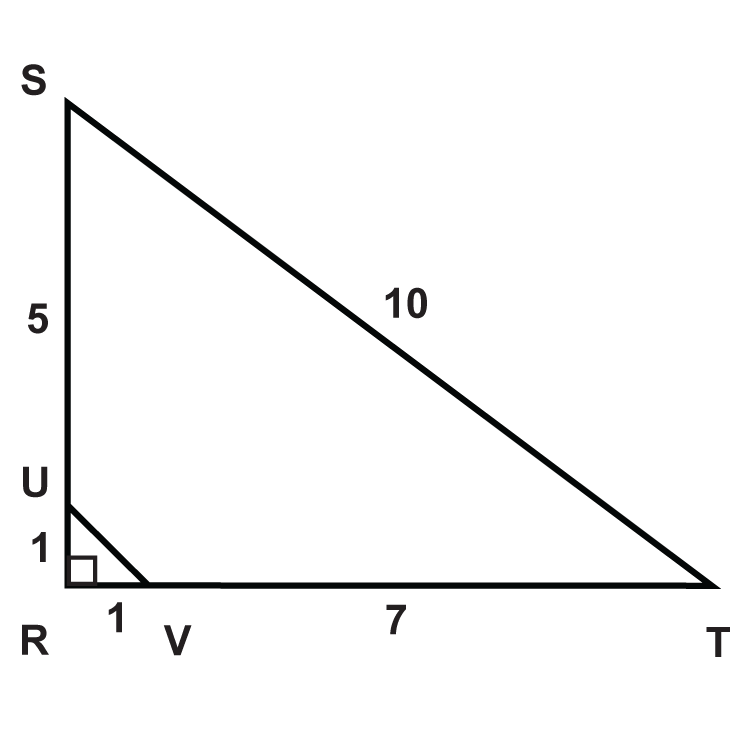
  ::查找使两个三角形相似的缺失变量值。

  3. 
  4. 
  5. 

  播放段落

  Determine if the triangles are similar. If so, write the similarity theorem and statement.
  ::确定三角形是否相似。 如果是, 请写入相似的定理和语句 。

  播放段落
  6. $\begin{align*}\Delta ABC\end{align*}$ is a right triangle with legs that measure 3 and 4. $\begin{align*}\Delta DEF\end{align*}$ is a right triangle with legs that measure 6 and 8.
     ::ABC是右三角形,腿的尺寸为3和4。 ZDEF是右三角形,腿的尺寸为6和8。
  播放段落
  7. $\begin{align*}\Delta GHI\end{align*}$ is a right triangle with a leg that measures 12 and a hypotenuse that measures 13. $\begin{align*}\Delta JKL\end{align*}$ is a right triangle with legs that measure 1 and 2.
     ::“GHI”是一个右三角形,右三角形的腿测量12度,下三角形测量13度。“JKL”是一个右三角形,右三角形的腿测量1和2度。
  8. 
  9. 
  10. 
  播放段落
  11. $\begin{align*}\overline{AC} = 3\end{align*}$ and  $\begin{align*}\overline{DF} = 6\end{align*}$  
      ::AC=3和DF=6 AC=3和DF=6

  

  12. 
  13. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源