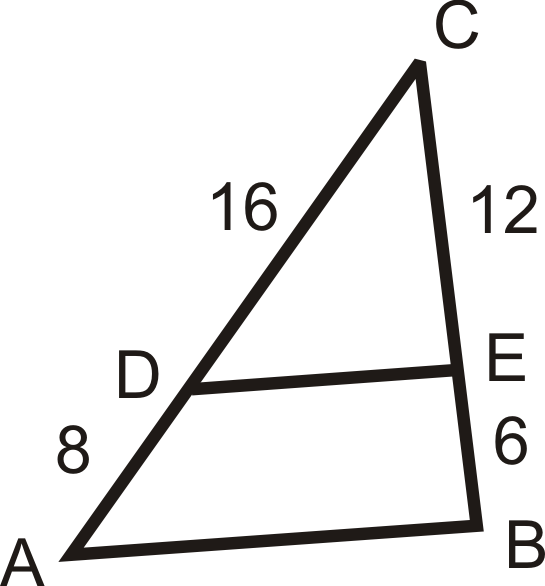7.8 三角相对性
章节大纲
-
Triangle Proportionality Theorem
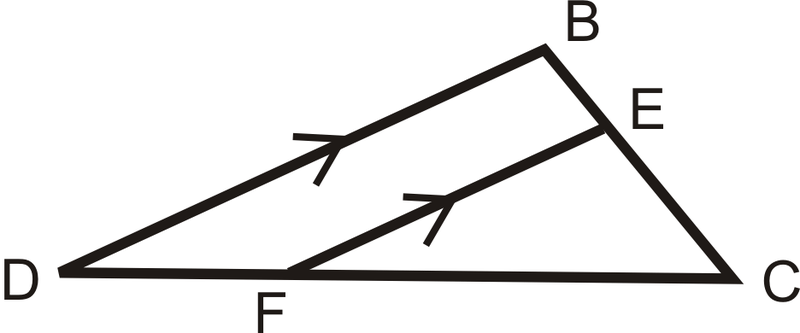
::三角交配性定理Think about a midsegment of a triangle . A midsegment is parallel to one side of a triangle and divides the other two sides into congruent halves. The midsegment divides those two sides proportionally. But what about another line that is parallel, but does not divide the other two sides into congruent halves? In fact, such a line will still divide the sides proportionally. This is called the Triangle Proportionality Theorem .
::想象一下三角形的中间部分。 中间部分与三角形的一边平行, 将另外两边分割成两半。 中间部分将这两边按比例分割。 但是, 另一条线是平行的, 而不是将另外两边分割成两半。 事实上, 这样一条线仍然会按比例分割两边。 这叫做三角形比例定理 。Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
::三角比例定理:如果一条直线与三角形一面平行的直线相互交错,则该直线将两侧按比例分割。If , then . ( is also a true proportion . )
:DABD=ECBE也是真实比例。 )
The converse of this theorem is also true.
::这一定理的反义也是对的。Triangle Proportionality Theorem Converse : If a line divides two sides of a triangle proportionally, then it is parallel to the third side.
::三角对称性理论对立:如果一条线按比例分割三角形两侧,则与第三侧平行。If , then .
::如果BDDA=BEEC, 那么DE AC'。What if you were given a triangle with a line segment drawn through it from one side to the other? How could you use information about the triangle's side lengths to determine if that line segment is parallel to the third side?
::如果给您一个三角形, 从一面拖过一条线段到另一面? 您如何使用三角形侧边长度的信息来确定该线段是否与第三面平行 ?Examples
::实例Use the diagram to answers Examples 1 and 2. .
::使用图表解答例1和例2, DB FE'。Example 1
::例1Name the similar triangles . Write the similarity statement.
::命名相似的三角形。写相近声明。
::* DBC*FECExample 2
::例2
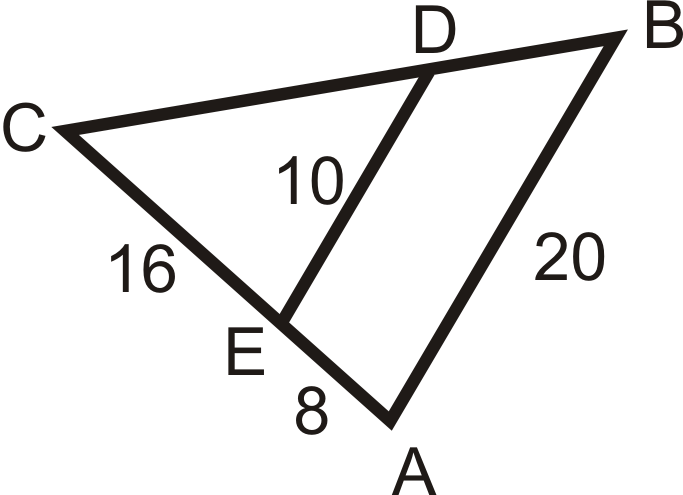
::FC+? FC==? FEFA=? FC+? FC=? FFE=?DF; DB
::DF; DB 的 DF; DBExample 3
::例3A triangle with its midsegment is drawn below. What is the ratio that the midsegment divides the sides into?
::一个带有中间部分的三角形画在下面。中间部分将两侧分割成什么比例?The midsegment splits the sides evenly. The ratio would be 8:8 or 10:10, which both reduce to 1:1.
::中间部分将两侧均匀分割。 比例为 8: 8 或 10: 10, 两者均降至 1:1 。Example 4
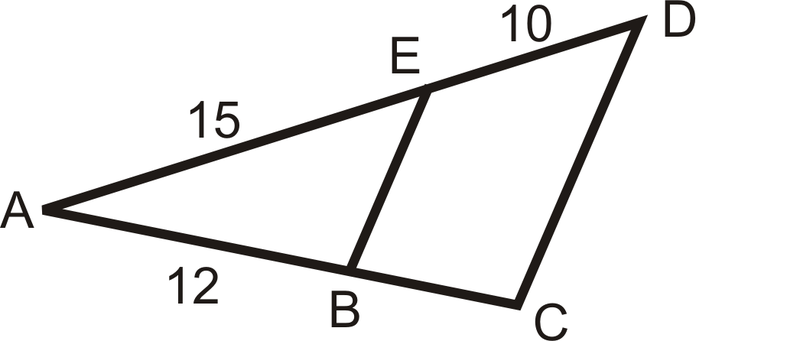
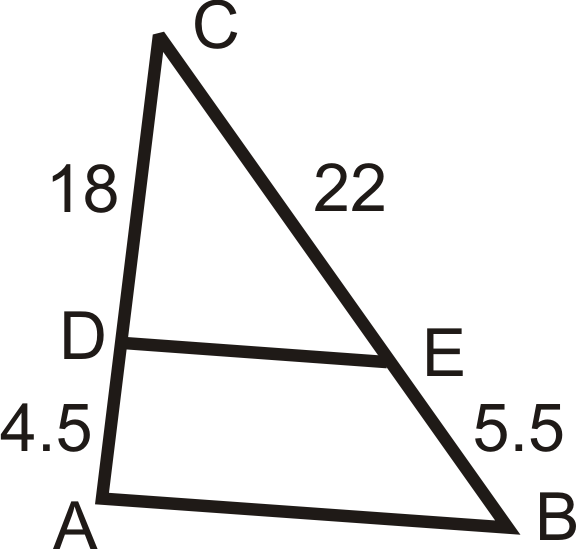
::例4In the diagram below, . Find .
::在下图中,EB CD 找到BCTo solve, set up a proportion.
::要解决, 设定比例 。
::1015=BC1215(BC)=120BC=8Example 5
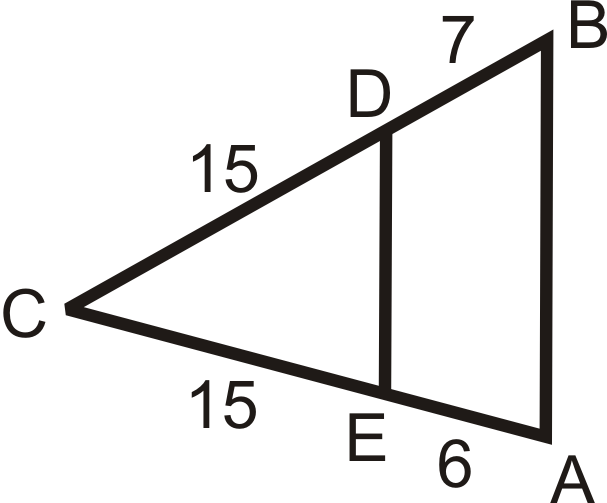
::例5Is ?
::德・・・・・・・・・・If the ratios are equal, then the lines are parallel.
::如果比率相等,则线线平行。Because the ratios are equal, .
::因为比率是相等的, DE・CB'。Review
::回顾Use the diagram to answer questions 1-7. .
::用图解答问题1 -7-
Find
.
::找到BD. 找到BD. 找到BD. -
Find
.
::寻找DC。 -
Find
.
::寻找DE。 -
Find
.
::寻找AC。 -
What is
?
::什么是BD:DC? -
What is
?
::DC:BC是什么? -
Why
?
::为什么是BC?
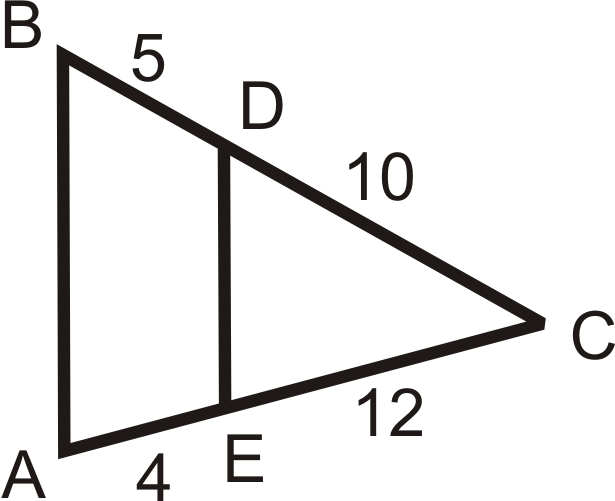
Use the given lengths to determine if .
::使用给定长度来确定是否AB===========================================================================================================================================================Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。Resources
::资源 -
Find
.