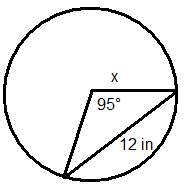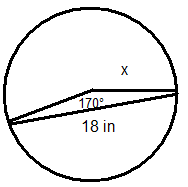Course: 2.7 弦的长度 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 弦的长度

Collapse Expand
弦的长度
You have been asked to help the younger students at your school with their Physical Education class. While working one afternoon, you are asked to take out a parachute that the students can play with. As the students are playing, one of them walks across a small portion of the parachute instead of under it like she is supposed to. If the chute is shaped like a circle with a radius of 6 meters, and the path the student walked across the chute covered an angle of $\begin{align*}50^\circ\end{align*}$ , what is the length of the path she walked across the parachute?
::有人要求你帮助学校的年轻学生上体育课。在下午工作时,你被要求拿出学生可以玩的降落伞。当学生们在玩耍时,其中一人走过降落伞的一小部分,而不是像她想象的那样在降落伞下。如果降落伞的形状像圆形一样,半径为6米,而学生们穿过降落伞的路径覆盖了50英寸的角,那么她穿过降落伞的路长度是多少?

Length of a Chord
::弦的长度

You may recall from your Geometry studies that a chord is a segment that begins and ends on a circle.
::从你的几何研究中你可能记得和弦是圆上开始和结束的部分

$\begin{align*}\overline{AB}\end{align*}$ is a chord in the circle.
::AB是圆圈的和弦

We can calculate the length of any chord if we know the angle measure and the length of the radius. Because each endpoint of the chord is on the circle, the distance from the center to $\begin{align*}A\end{align*}$ and $\begin{align*}B\end{align*}$ is the same as the radius length.
::如果我们知道角度量和半径长度,我们可以计算任何和弦的长度。因为和弦的每个端点都在圆上,从中间到A和B的距离与半径长度相同。

Next, if we bisect the angle, the angle bisector must be perpendicular to the chord and bisect it (we will leave the proof of this to your Geometry class). This forms a right triangle.
::接下来,如果我们将角度分成两部分, 角两部分必须与和弦垂直, 并且将它分为两部分( 我们将把证据留给您的几何等级) 。这将形成一个右三角。

We can now use a simple sine ratio to find half the chord, called $\begin{align*}c\end{align*}$ here, and double the result to find the length of the chord.
::我们现在可以用一个简单的正弦比来找到一半的和弦, 叫C在这里, 并翻倍的结果来找到和弦的长度。

$\begin{aligned} \sin \frac{θ}{2} = \frac{c}{r} \\ c = r \times \sin \frac{θ}{2} \end{aligned}$
$\begin{align*}& \sin \frac{\theta}{2}=\frac{c}{r}\\ & c=r \times \sin \frac{\theta}{2}\end{align*}$
::sin% 2 = crc=rxsin% 2 = crc=rrxsin

So the length of the chord is:
::所以和弦的长度是:

$\begin{aligned} 2 c = 2 r \sin \frac{θ}{2} \end{aligned}$
$\begin{align*}2c=2r \sin \frac{\theta}{2}\end{align*}$
::2c=2rsin=2

Finding the Length of a Chord
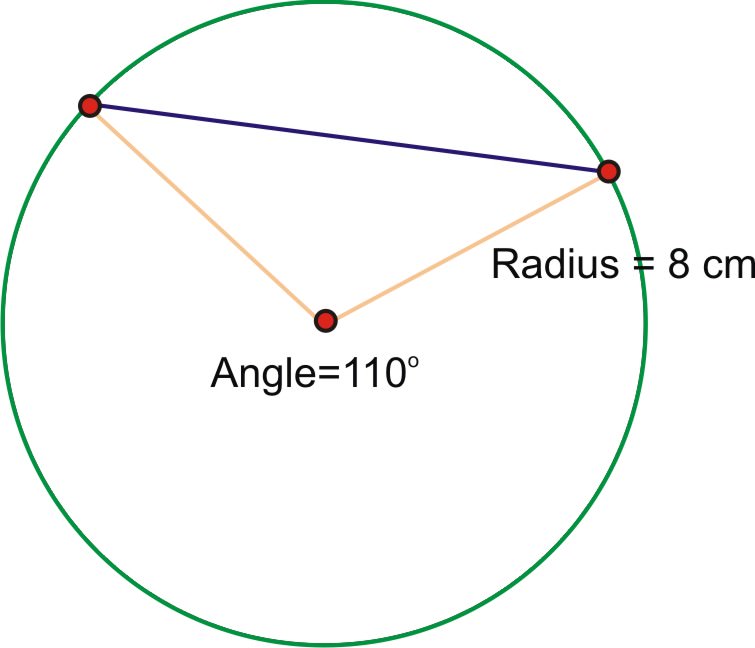
::查找弦的长度

1. Find the length of the chord of a circle with radius 8 cm and a central angle of $\begin{align*}110^\circ\end{align*}$ . Approximate your answer to the nearest mm.
::1. 查找圆圆的和弦长度,圆半径8厘米,中角110英寸。答案接近最接近的毫米。

We must first convert the angle measure to radians:
::我们必须首先将角度量度转换为弧度 :

$\begin{aligned} 110 \times \frac{π}{180} = \frac{11 π}{18} \end{aligned}$
$\begin{align*}110 \times \frac{\pi}{180}=\frac{11\pi}{18}\end{align*}$

Using the formula, half of the chord length should be the radius of the circle times the sine of half the angle.
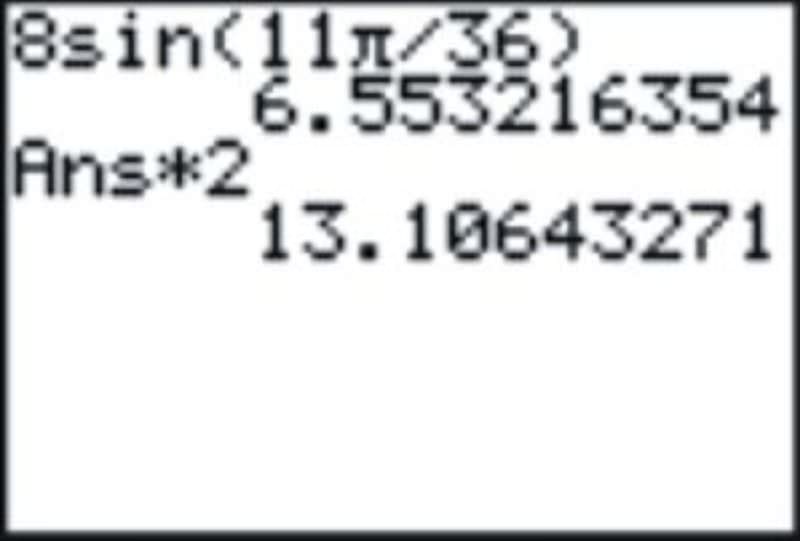
::使用公式,弦长度的一半应该是圆半径乘角的正弦值。

$\begin{aligned} \frac{11 π}{18} \times \frac{1}{2} = \frac{11 π}{36} \\ 8 \times \sin \frac{11 π}{36} \end{aligned}$
$\begin{align*}& \frac{11\pi}{18} \times \frac{1}{2}=\frac{11\pi}{36}\\ & 8 \times \sin \frac{11\pi}{36}\end{align*}$
::1118×12=11368×sin1136

Multiply this result by 2.
::乘以这个结果乘以 2。

So, the length of the chord is approximately 13.1 cm.
::因此,和弦长度约为13.1厘米。

2. Find the length of the chord of a circle with a radius of 2 m that has a central angle of $\begin{align*}90^\circ\end{align*}$ .
::2. 查找圆圆的和弦长度,半径为2米,中心角为90。

First convert the angle to radians:
::首先将角度转换为弧度 :

$\begin{aligned} 90 \times \frac{π}{180} = \frac{π}{2} \end{aligned}$
$\begin{align*}90 \times \frac{\pi}{180}=\frac{\pi}{2}\end{align*}$

Using the formula, half of the chord length should be the radius of the circle times the sine of half the angle.
::使用公式,弦长度的一半应该是圆半径乘角的正弦值。

$\begin{aligned} \frac{π}{2} \times \frac{1}{2} = \frac{π}{4} \\ 2 \times \sin \frac{π}{4} \end{aligned}$
$\begin{align*}& \frac{\pi}{2} \times \frac{1}{2}=\frac{\pi}{4}\\ & 2 \times \sin \frac{\pi}{4}\end{align*}$
::2x1242×sin4

Multiply this result by 2.
::乘以这个结果乘以 2。

So the answer is approximately 2.83 meters.
::答案大约是2.83米

3. Find the length of the chord of a circle with radius 1 m and a central angle of $\begin{align*}170^\circ\end{align*}$ .
::3. 查找圆的和弦长度,半径1米,中角170。

We must first convert the angle measure to radians:
::我们必须首先将角度量度转换为弧度 :

$\begin{aligned} 170 \times \frac{π}{180} = \frac{17 π}{18} \end{aligned}$
$\begin{align*}170 \times \frac{\pi}{180}=\frac{17\pi}{18}\end{align*}$

Using the formula, half of the chord length should be the radius of the circle times the sine of half the angle.
::使用公式,弦长度的一半应该是圆半径乘角的正弦值。

$\begin{aligned} \frac{17 π}{18} \times \frac{1}{2} = \frac{17 π}{36} \\ 1 \times \sin \frac{17 π}{36} = .996 \end{aligned}$
$\begin{align*}& \frac{17\pi}{18} \times \frac{1}{2}=\frac{17\pi}{36}\\ & 1 \times \sin \frac{17\pi}{36} = .996\end{align*}$
::1718×12=17361×sin1736=.996

Multiply this result by 2.
::乘以这个结果乘以 2。

So, the length of the arc is approximately 1.992
::所以弧的长度大约是1.992

Notice that the length of the chord is almost 2 meters, which would be the diameter of the circle. If the angle had been 180 degrees, the chord would have just been the distance all the way across the circle going through the middle, which is the diameter.
::注意和弦的长度接近2米, 也就是圆的直径。如果角度是180度, 和弦的长度就是圆的距离, 穿过圆的中间, 也就是直径。

Examples
::实例

Example 1
::例1

Earlier, you were asked what is the length of the path she walked across the parachute.
::之前有人问过你她穿过降落伞的路程有多长

With the equation for the length of a chord in hand, you can calculate the distance the student ran across the parachute:
::用手头的和弦长度方程式, 您可以计算学生穿越降落伞的距离 :

First convert the measure in degrees to radians:
::先将度量转换为弧度:

$\begin{align*}50 \times \frac{\pi}{180} \approx .27\pi\end{align*}$

$\begin{align*}2r \sin \frac{\theta}{2} = (2)(6) \sin \frac{.27\pi}{2} = 12 \sin .135\pi \approx 4.94 meters\end{align*}$
::2rsin2=(2)(6)(6)(6)272=12sin1354.94公尺

Example 2
::例2

If you run a piece of string across a doughnut you are eating, and the radius between the endpoints of the string to the center of the doughnut is 4 inches, how long is the string if the angle swept out by the chord is $\begin{align*}20^\circ\end{align*}$ ?
::如果你在吃一个甜甜圈上运行一个字符串, 而线条端点与甜甜圈中间之间的半径是4英寸, 如果弦的角被合唱团冲出是20英寸, 弦的半径是多久?

You can use the equation $\begin{align*}C = 2r\sin \left( \frac{\theta}{2} \right)\end{align*}$ to solve this problem: (Don't forget to convert angles to radians)
::您可以使用方程式 C=2rsin {{{{{{{}} (%2) 来解决这个问题不要忘记将角度转换为弧度)

$\begin{aligned} C = 2 r \sin (\frac{θ}{2}) \\ C = (2) (4) \sin (\frac{.349}{2}) \\ C = 8 (.1736) \\ C = 1.388 \\ i n c h e s \end{aligned}$
$\begin{align*} C = 2r\sin \left( \frac{\theta}{2} \right)\\ C = (2)(4)\sin \left( \frac{.349}{2} \right)\\ C = 8(.1736)\\ C = 1.388\\ inches \end{align*}$
::C=2rsin(2)C=(2)(4)sin(.3492)C=8(1736)C=1.388英寸

Example 3
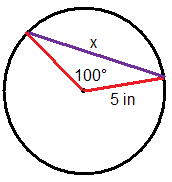
::例3

You are eating dinner one night with your family at the local Italian restaurant. A piece of spaghetti makes a chord across your plate. You know that the length of the spaghetti strand is 5 inches, and the radius of the plate is 7 inches. What is the angle swept out by the chord?
::你知道意大利面条长度是5英寸,盘子半径是7英寸。什么角度被和弦冲出?

Since the radius of the plate and the length of the chord are known, you can solve for the angle:
::由于已知道板盘的半径和和弦长度,您可以解答角度 :

$\begin{aligned} C = 2 r \sin (\frac{θ}{2}) \\ \frac{C}{2 r} = \sin (\frac{θ}{2}) \\ \sin^{- 1} (\frac{c}{2 r}) = \frac{θ}{2} \\ \sin^{- 1} (\frac{5}{14}) = \frac{θ}{2} \\ .365 = \frac{θ}{2} \\ θ = .73 \end{aligned}$
$\begin{align*} C = 2r\sin \left( \frac{\theta}{2} \right)\\ \frac{C}{2r} = \sin \left( \frac{\theta}{2} \right)\\ \sin^{-1} \left( \frac{c}{2r} \right) = \frac{\theta}{2}\\ \sin^{-1} \left( \frac{5}{14} \right) = \frac{\theta}{2}\\ .365 = \frac{\theta}{2}\\ \theta = .73\\ \end{align*}$
::C=2rsin(2)C2r=sin(2)sin-1(2r)2sin-11(514)2.365273。

The angle spanned by the spaghetti is .73 radians.
::意大利面的角宽度是.73弧度。

Example 4
::例4

If you draw a chord across a circle and make a chord across it that has a length of 15 inches, sweeping out an angle of $\begin{align*}\pi\end{align*}$ radians, what is the radius of the circle you drew?
::如果在圆上画一条和弦,然后在圆上画一条长度为15英寸的和弦,扫出弧度角,那么您画的圆的半径是多少?

Using the equation for the length of a chord:
::用方程式来表示和弦的长度 :

$\begin{aligned} c = 2 r \sin (\frac{θ}{2}) \\ 15 = (2 r) \sin (\frac{π}{2}) \\ r = 7.5 \end{aligned}$
$\begin{align*} c = 2r\sin \left( \frac{\theta}{2} \right)\\ 15 = (2r)\sin \left( \frac{\pi}{2} \right)\\ r = 7.5\\ \end{align*}$
::c=2rsin(2)15=(2r)sin(2r=7.5)

As you can see, the radius of the circle is 7.5 inches. This is what you should expect, since the chord sweeps out an angle of $\begin{align*}\pi\end{align*}$ . This means that it sweeps out half of the circle, so that the chord is actually going across the whole diameter of the circle. So if the chord is going across the diameter and has a length of 15 inches, then the radius of the circle should be 7.5 inches.
::正如您所看到的,圆的半径是7.5英寸。这是您应该期望的, 因为和弦扫出的角。这意味着它扫出圆的半径, 所以和弦实际上横跨圆的整个直径。所以如果和弦横穿直径, 长度为15英寸, 那么圆的半径应该是7.5英寸。

Review
::回顾

Find the length of the chord of a circle with radius 1 m and a central angle of $\begin{align*}100^\circ\end{align*}$ .
::查找圆的和弦长度,圆半径为1米,中心角为100。

Find the length of the chord of a circle with radius 8 km and a central angle of $\begin{align*}130^\circ\end{align*}$ .
::查找圆的和弦长度,圆半径为8公里,中心角为130。

Find the length of the chord of a circle with radius 4 in and a central angle of $\begin{align*}45^\circ\end{align*}$ .
::查找圆的和弦长度,圆的半径 4 英寸,中角 45 。

Find the length of the chord of a circle with radius 3 ft and a central angle of $\begin{align*}32^\circ\end{align*}$ .
::查找圆的和弦长度,圆半径为3英尺,中心角为32英寸。

Find the length of the chord of a circle with radius 2 cm and a central angle of $\begin{align*}112^\circ\end{align*}$ .
::查找圆的和弦长度,圆半径为2厘米,中心角为112。

Find the length of the chord of a circle with radius 7 in and a central angle of $\begin{align*}135^\circ\end{align*}$ .
::查找圆的和弦长度,圆半径7英寸,中心角135。

Solve for the missing variable in each circle.
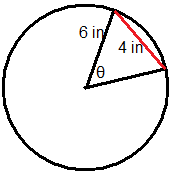
::解决每个圆圈中缺失的变量。

Use the picture below for questions 13-15.
::问题13-15请使用下面的图片。

Suppose you knew the length of the chord, the length of the radius, and the central angle of the above circle. Describe one way to find the length of the red segment using the Pythagorean Theorem.
::假设您知道和弦的长度, 半径的长度, 以及上面圆的中心角。描述使用 Pythagorean Theorem 找到红段长度的方法。

Suppose you knew the length of the chord, the length of the radius, and the central angle of the above circle. Describe one way to find the length of the red segment using cosine.
::假设您知道和弦的长度, 半径的长度, 以及上面圆的中心角。描述一个使用 cosine 找到红段长度的方法。

What would you need to know in order to find the area of the circle segment (the portion of the circle between the chord and the edge of the circle)? Describe how to find the area of this region.
::您需要知道什么才能找到圆段的区域( 圆和圆边缘之间的圆段部分) ? 描述如何找到这个区域的区域。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

弦的长度

Length of a Chord ::弦的长度

Finding the Length of a Chord ::查找弦的长度

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Length of a Chord
::弦的长度

Finding the Length of a Chord
::查找弦的长度

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)