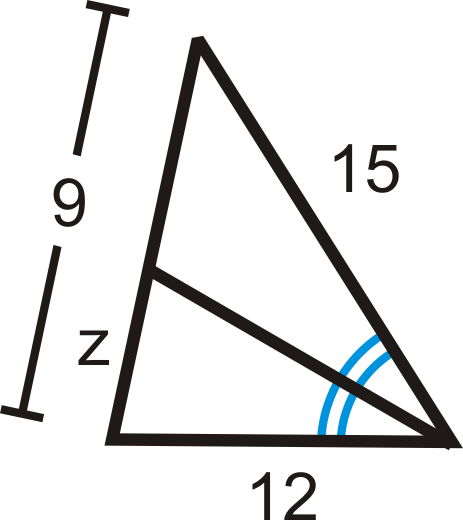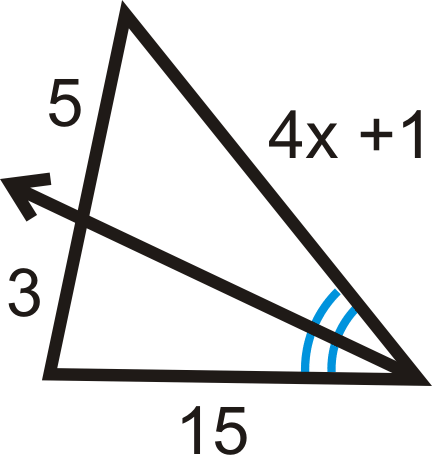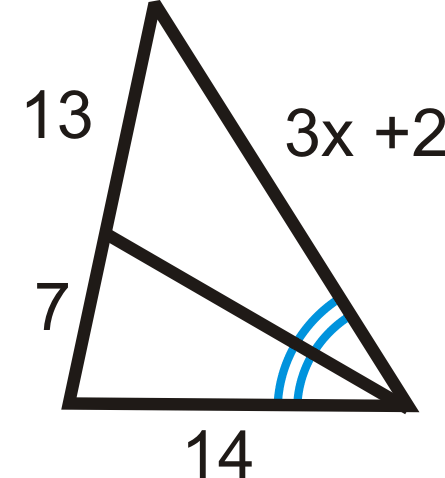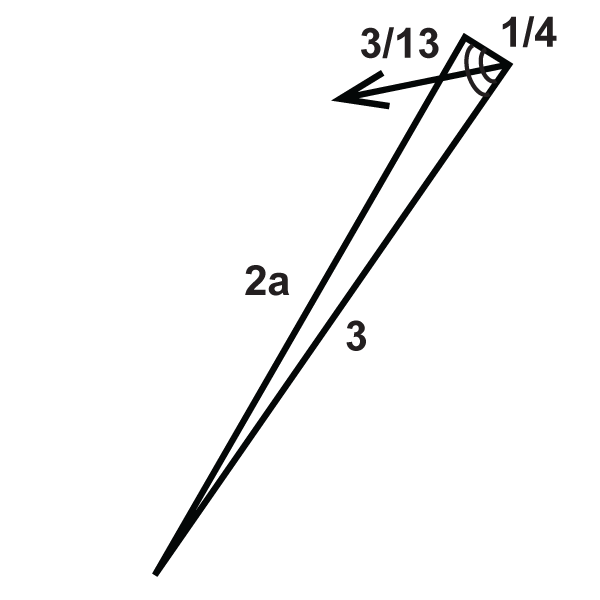Section outline

  • General

    Collapse all Expand all

  • 带有角分区的比例比例

    Angle Bisector Theorem
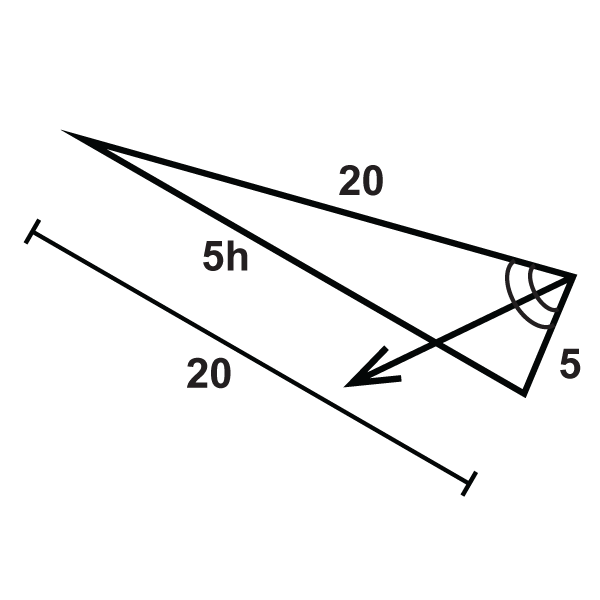
    ::角双两区定理

    When an angle within a triangle is bisected, the bisector divides the triangle proportionally. This idea is called the Angle Bisector Theorem .
    ::当三角形内的角被双切时, 分区会按比例分割三角形 。 这个想法叫做 Agle 双区定理 。

    Angle Bisector Theorem: If a ray bisects an angle of a triangle, then it divides the opposite side into segments that are proportional to the lengths of the other two sides. 
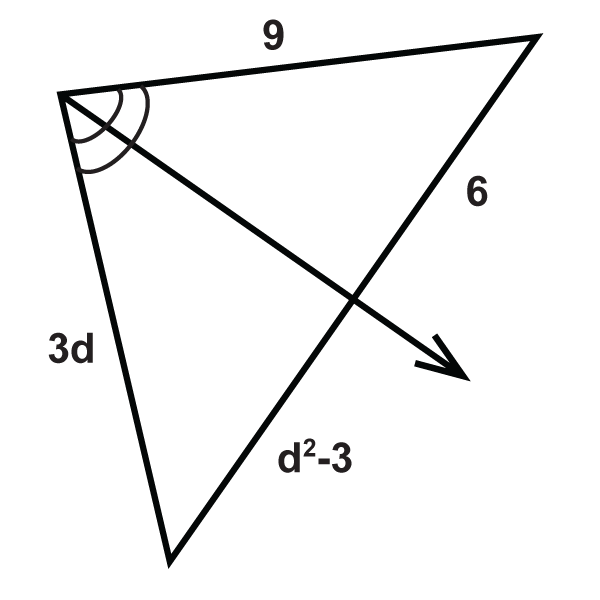
    ::角双区定理:如果一射线两截成三角形角,则将对面分为与另外两侧长度成正比的区段。

    If △ B A C ∼ △ C A D , then B C C D = A B A D .
    ::如果BACCAD,那么BCD=ABAD。

    What if you were told that a ray was an angle bisector of a triangle? How would you use this fact to find unknown values regarding the triangle's side lengths?
    ::如果有人告诉你射线是三角形的角角对角部分呢?你如何利用这个事实来发现三角形侧边长度的未知值?

    Examples
    ::实例

    Example 1
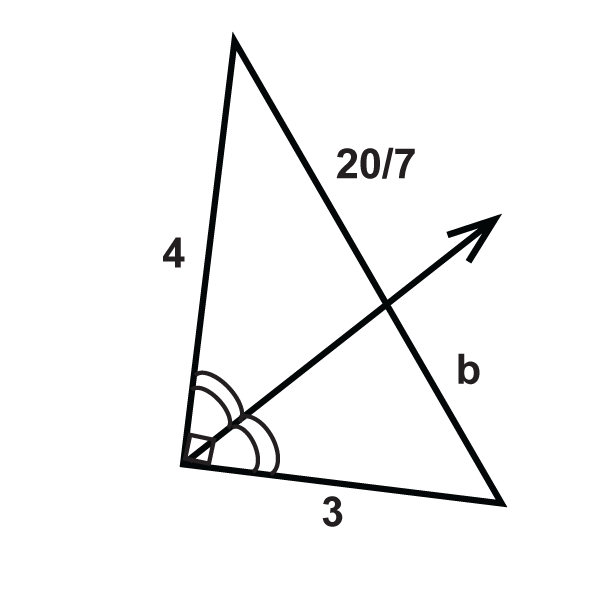
    ::例1

    Fill in the missing variable:
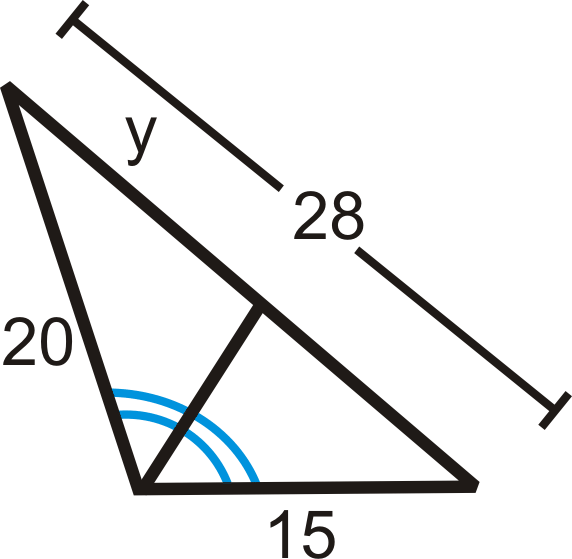
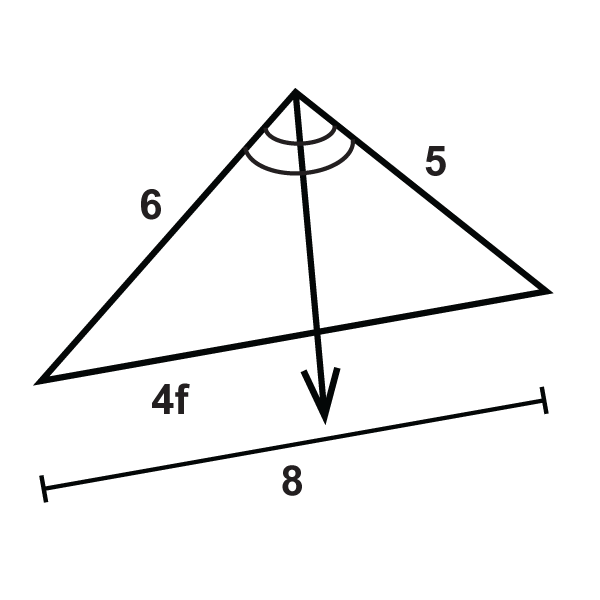
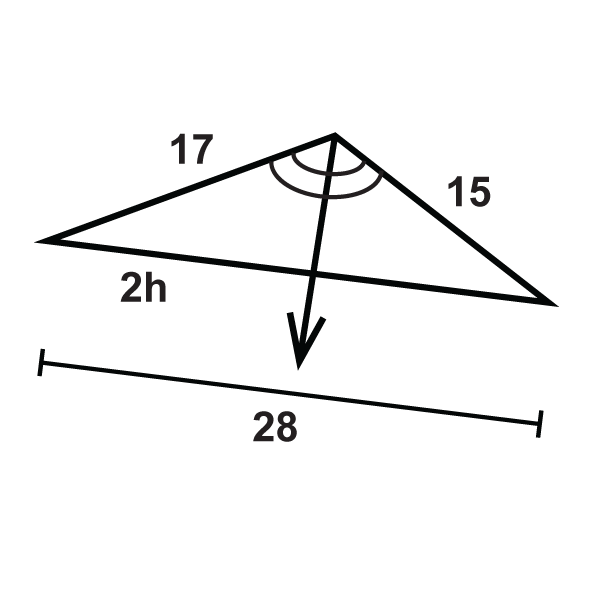
    ::填充缺失变量 :

    Set up a proportion and solve.
    ::设定一个比例并解决。

    20 y = 15 28 − y 15 y = 20 ( 28 − y ) 15 y = 560 − 20 y 35 y = 560 y = 16

    ::20y=1528-yy15y=20(28-y)15y=560-20y35y=560y=16

    Example 2
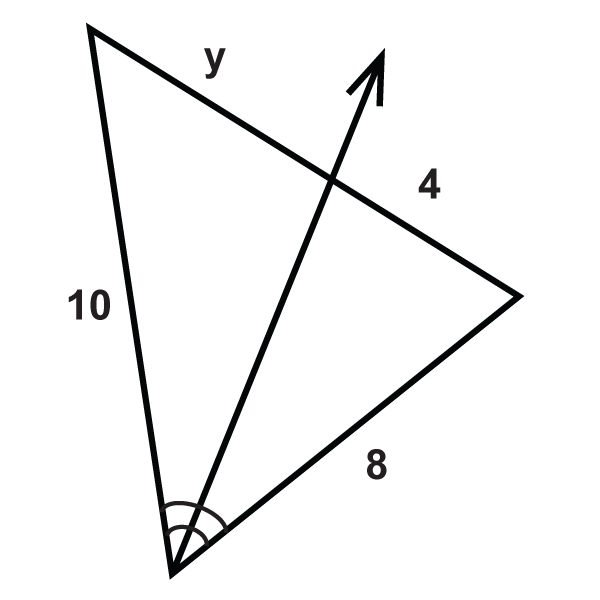
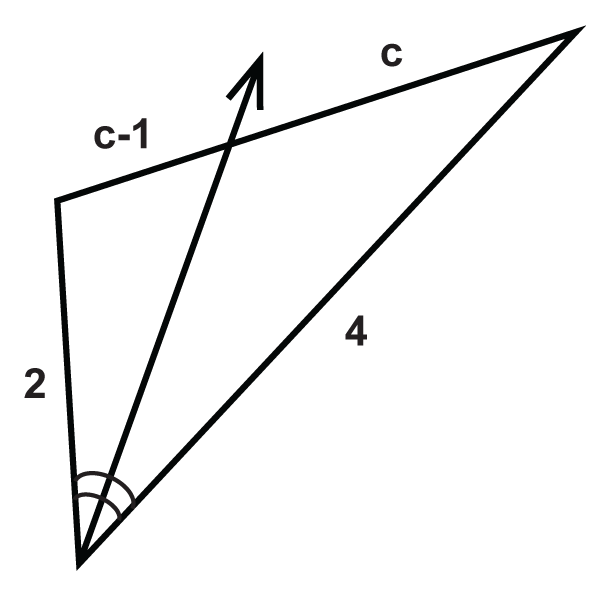
    ::例2

    Fill in the missing variable:
    ::填充缺失变量 :

    Set up a proportion and solve.
    ::设定一个比例并解决。

    12 z = 15 9 − z 15 z = 12 ( 9 − z ) 15 z = 108 = 12 z 27 z = 108 z = 4

    ::12z=159-z15z=12(9-z)15z=108=12z27z=108z=4

    Example 3
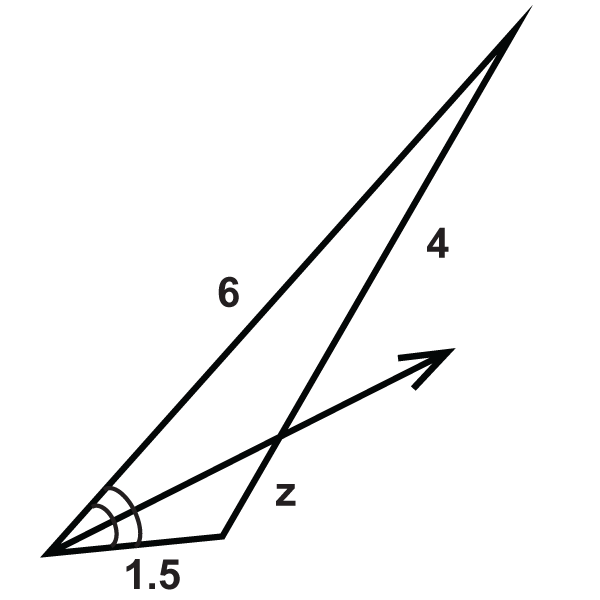
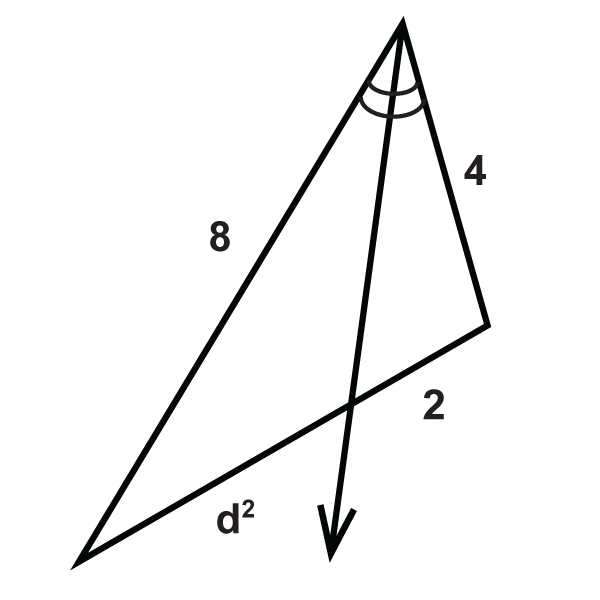
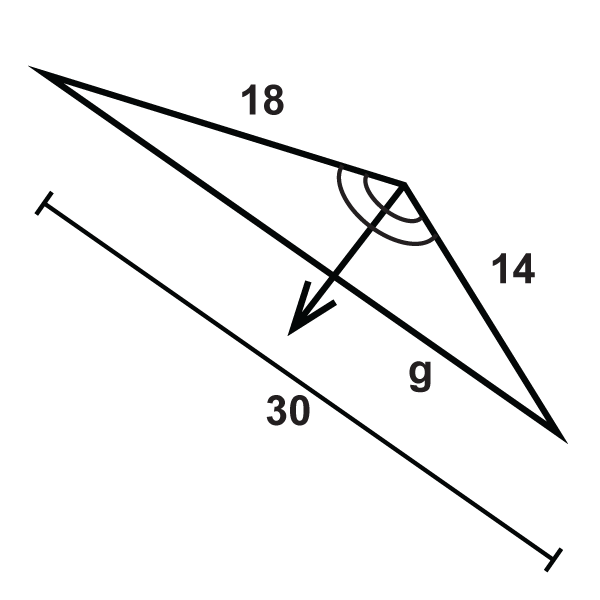
    ::例3

    Find x .
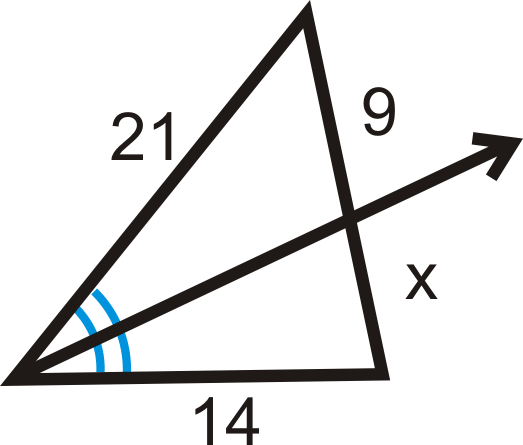
    ::查找 x.

    The ray is the angle bisector and it splits the opposite side in the same ratio as the other two sides. The proportion is:
    ::射线是角度的对角,它与其他两边的对面以相同比例分裂。 比例是:

    9 x = 21 14 21 x = 126 x = 6

    ::9x=211421x=126x=6

    Example 4
    ::例4

    Find the value of x that would make the proportion true.
    ::查找 x 的值, 使比例变为真实 。

    You can set up this proportion like the previous example.
    ::您可以像上一个示例一样设置此比例 。

    5 3 = 4 x + 1 15 75 = 3 ( 4 x + 1 ) 75 = 12 x + 3 72 = 12 x 6 = x

    ::53=4x+11575=3(4x+1)75=12x+372=12x6=x

    Example 5
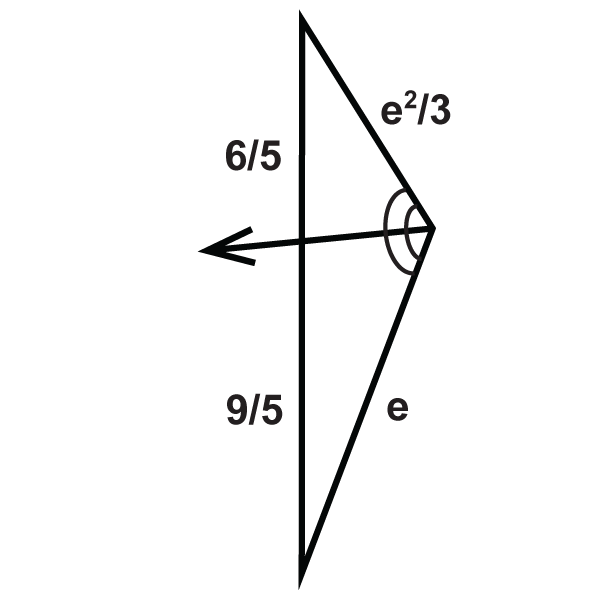
    ::例5

    Find the missing variable:
    ::查找缺失变量 :

    Set up a proportion and solve like in the previous examples.
    ::设置比例和解析, 如在前一例中 。

    12 4 = x 3 36 = 4 x x = 9

    ::124=x336=4xx=9

    Review
    ::回顾

    Find the value of the missing variable(s).
    ::查找缺失变量的值。

    Solve for the unknown variable. Round your answers to the nearest hundredths place.
    ::解决未知变量。 将您的答案转至最近的一百个位置 。

    Review (Answers)
    ::回顾(答复)

    Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
    ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

    Resources
    ::资源