Course: 2.9 松树和大豆石图

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section Sine 和 Cosescant 图形

Collapse Expand
Sine 和 Cosescant 图形
Imagine for a moment that you have a clock that has only one hand - that rotates counterclockwise! However, the hand is very slim all the way until the tip, where there is a ball on the end. In fact, the hand is so slim you won't notice it. You only notice the ball on the end of the rotating hand. This hand is rotating faster than normal. Here is a picture of the clock:
::想象一下, 你有一个只有一只手的时钟—— 即逆时旋转的时钟。但是, 手总是非常小, 直到尖端, 上面有一个球。事实上, 手是如此小, 你看不到它。您只注意到旋转手的末端的球。手的旋转速度比正常的要快。下面是时钟的图片 :

Consider what it would be like if you put a light next to the clock and let the shadow of the hands fall on the far wall.
::想想看,如果你把灯光放在时钟旁边,让手的影子落在远墙上,那会是什么样子。

What pattern would that shadow trace out? If you think about it, you might realize that the shadow would make an up and down motion, over and over as the hand of the clock rotated. Now imagine that instead of a wall, there was a large piece of paper for the shadow to fall on. And wherever the shadow fell, there would be a mark on the paper. Finally, imagine moving the paper as the clock rotates. Can you imagine sort of pattern this would trace out?
::阴影会追溯到什么模式? 如果你仔细想一想, 你可能会意识到, 阴影会随着钟的旋转而从上到下移动。现在想象一下, 与墙相反, 阴影会掉下一大块纸。无论影子落到哪里, 纸上都会留下一个标记。最后, 想象一下, 当钟旋转时, 纸会移动。你能想象一下, 这会追踪到什么模式吗 ?

Sine and Cosecant Graphs
::Sine 和 Cosescant 图形

By now, you have become very familiar with the specific values of sine, cosine, and tangents for certain angles of rotation around the coordinate grid. In mathematics, we can often learn a lot by looking at how one quantity changes as we consistently vary another. We will be looking at the sine value as a function of the angle of rotation around the coordinate plane. We refer to any such function as a circular function , because they can be defined using the unit circle . Recall from earlier sections that the sine of an angle in standard position is the ratio of $\begin{aligned} \frac{y}{r} \end{aligned}$ , where $\begin{aligned} y \end{aligned}$ is the $\begin{aligned} y - \end{aligned}$ coordinate of any point on the circle and $\begin{aligned} r \end{aligned}$ is the distance from the origin to that point.
::现在,您已经非常熟悉正弦、正弦、正弦和正弦的具体值, 以及坐标网周围某些旋转角度的具体值。在数学中, 我们通常可以通过查看一个数量的变化来学到很多东西, 当我们始终在另一个变化时。我们将将正弦值作为坐标平面周围旋转角度的函数来看待。我们把任何这样的函数都当作一个循环函数, 因为它们可以用单位圆来定义。回顾前面的章节, 标准位置角度的正弦值是 y 之比, y 是圆上任何点的Y- 坐标, r 是起始点到那个点的距离。

Because the ratios are the same for a given angle, regardless of the length of the radius $\begin{aligned} r \end{aligned}$ , we can use the unit circle as a basis for all calculations.
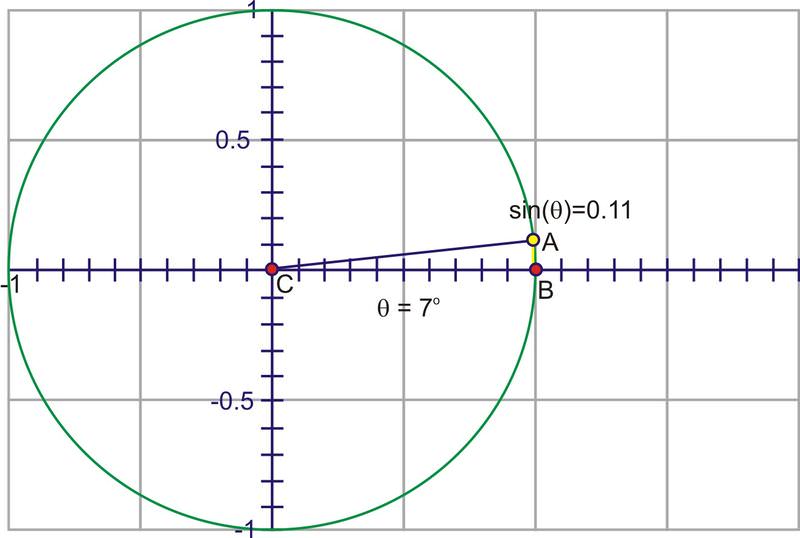
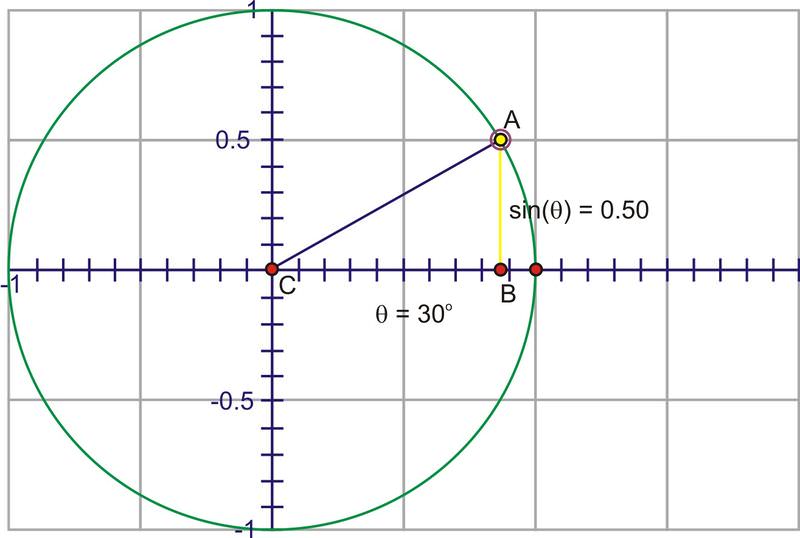
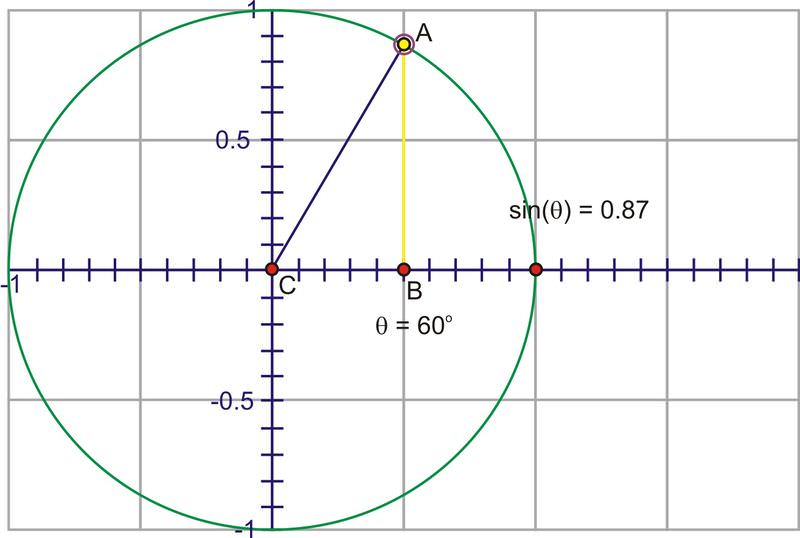
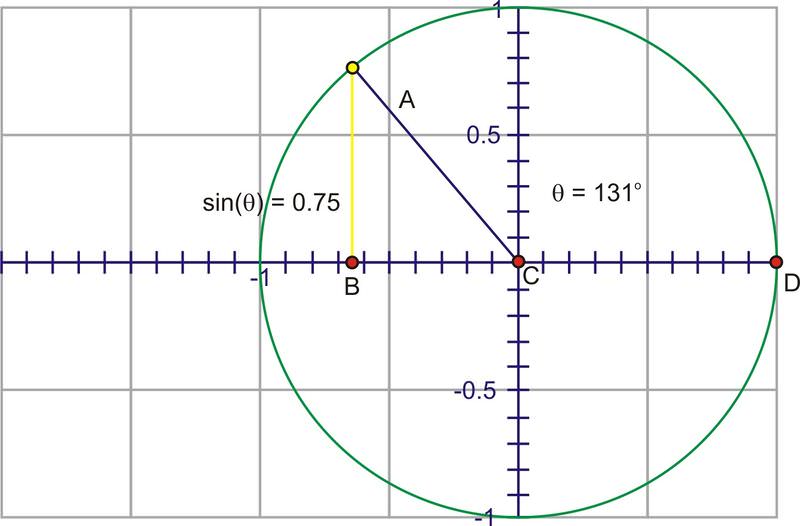
::因为对于某个角度,比率是一样的, 不论半径 r 的长度, 我们可以使用单位圆作为所有计算的基础。

The denominator is now 1, so we have the simpler expression, $\begin{aligned} \sin x = y \end{aligned}$ . The advantage to this is that we can use the $\begin{aligned} y - \end{aligned}$ coordinate of the point on the unit circle to trace the value of $\begin{aligned} \sin θ \end{aligned}$ through a complete rotation. Imagine if we start at 0 and then rotate counter-clockwise through gradually increasing angles. Since the $\begin{aligned} y - \end{aligned}$ coordinate is the sine value, watch the height of the point as you rotate.
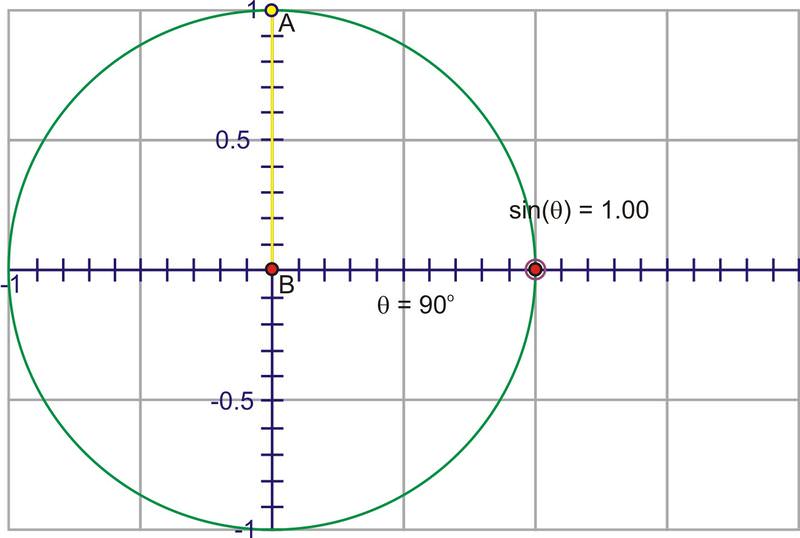
::分母为 1, 因此我们有一个简单的表达式, sinx=y。其优点是, 我们可以使用单位圆上的点的 Y - 坐标来通过一个完全旋转来追踪 sin 值。想象如果我们在 0 时开始, 然后反时针旋转, 通过逐渐增加的角度。由于 y - 坐标是正弦值, 请在旋转时注意点的高度。

Through Quadrant I that height gets larger, starting at 0, increasing quickly at first, then slower until the angle reaches $\begin{aligned} 90^{\circ} \end{aligned}$ , at which point, the height is at its maximum value, 1.
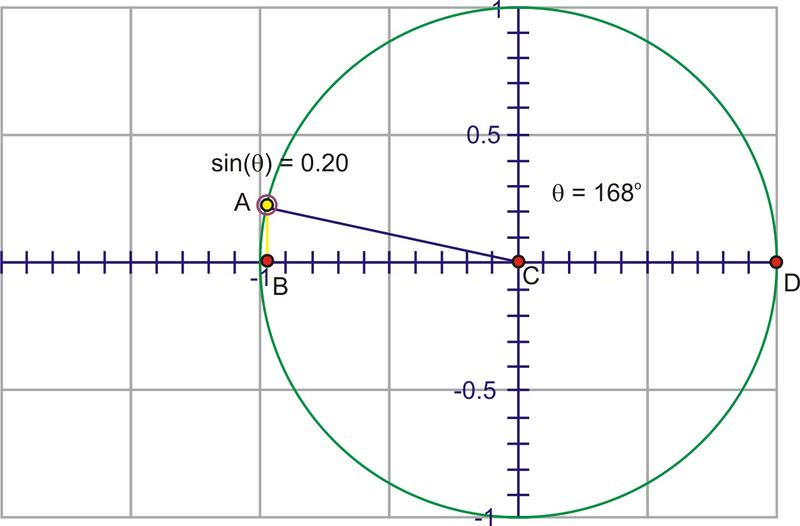
::通过 Quadrant I , 高度越高越大, 从0开始, 开始越快增长, 开始越快, 然后越慢, 直到角达到 90 , 在那个点, 高度是最大值, 1 。

As you rotate into the second quadrant, the height starts to decrease towards zero.
::当您旋转到第二个象限时,高度开始下降到零。

When you start to rotate into the third and fourth quadrants, the length of the segment increases, but this time in a negative direction, growing to -1 at $\begin{aligned} 270^{\circ} \end{aligned}$ and heading back toward 0 at $\begin{aligned} 360^{\circ} \end{aligned}$ .
::当您开始旋转到第三和第四方位时, 段的长度会增加, 但这一次向负方向, 在 270 ° 时增长到 - 1, 在 360 ° 时返回 0 。

After one complete rotation, even though the angle continues to increase, the sine values will repeat themselves. The same would have been true if we chose to rotate clockwise to investigate negative angles, and this is why the sine function is a periodic function . The period is $\begin{aligned} 2 π \end{aligned}$ because that is the angle measure before the sine of the angle will repeat its values.
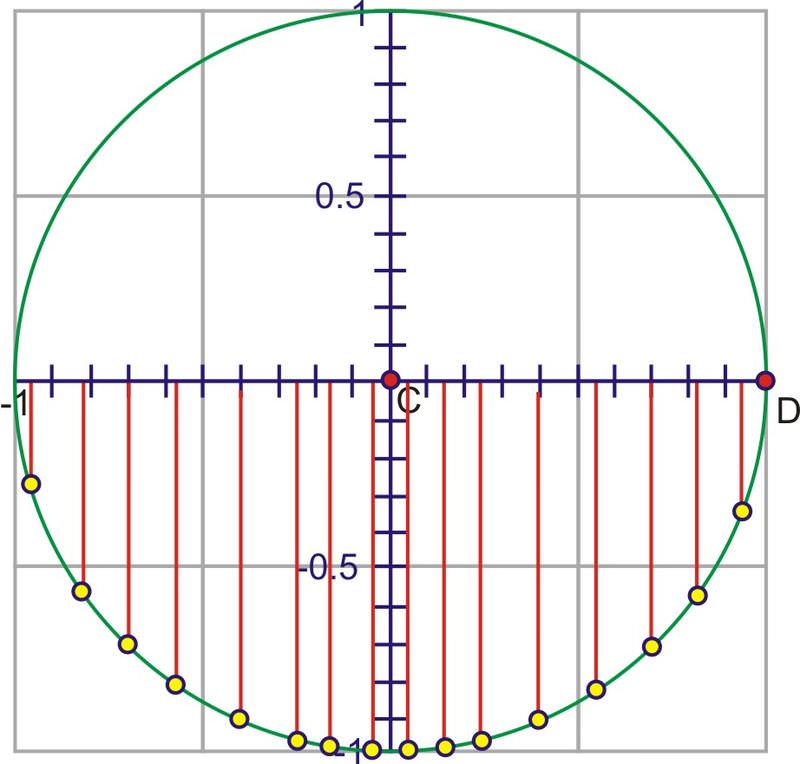
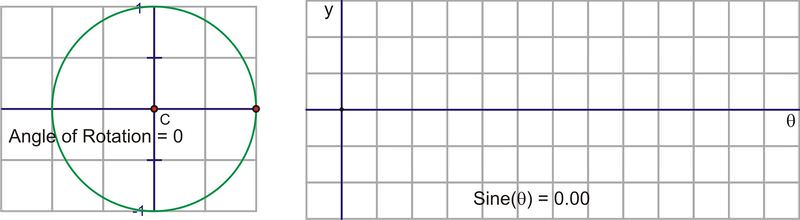
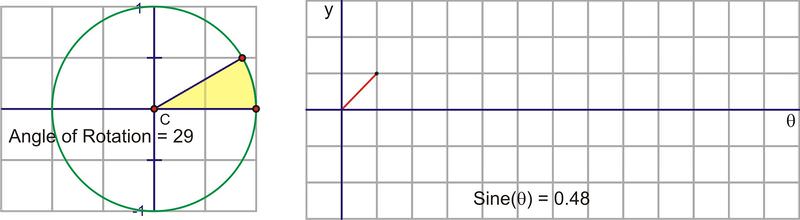
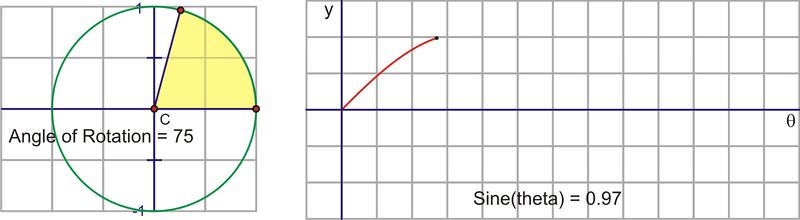
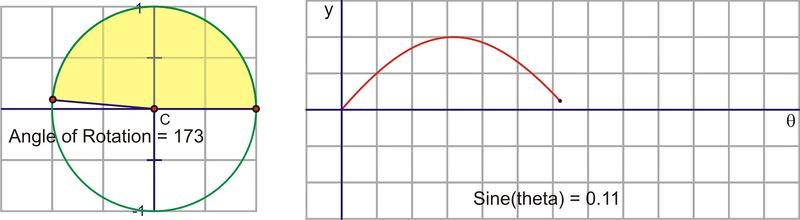
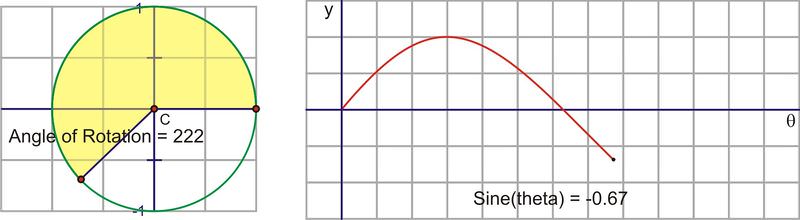
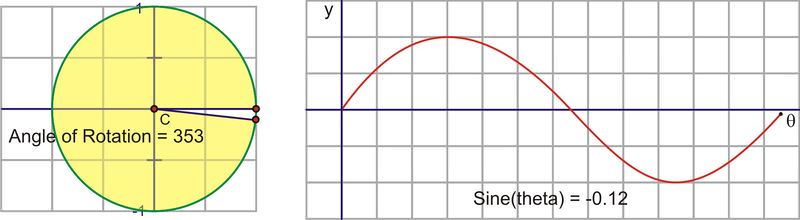
::一个完整的旋转后,即使角度继续增加,正弦值也会重复。如果我们选择顺时针旋转来调查负面角度,那么正弦值也会重复。这就是正弦函数是一个周期函数的原因。这个周期是 2+ , 因为角的正弦值会重复其值之前的角度测量值。

Let’s translate this circular motion into a graph of the sine value vs. the angle of rotation. The following sequence of pictures demonstrates the connection. These pictures plot $\begin{aligned} (θ, \sin θ) \end{aligned}$ on the coordinate plane as $\begin{aligned} (x, y) \end{aligned}$ .
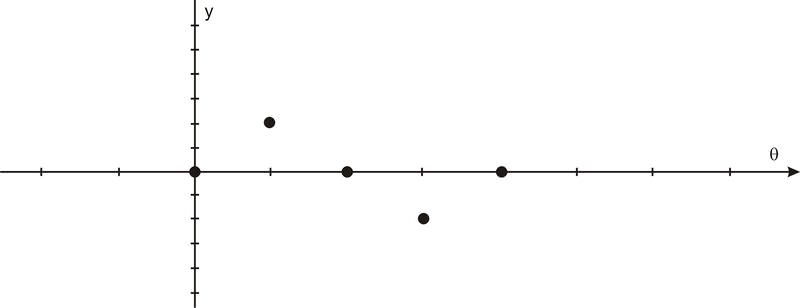
::让我们将这个圆形动作转换为正弦值与旋转角度的图形。以下的图片序列显示了连接。这些图片图( , sin) 以( x, y) 表示在坐标平面上的图( , sin) 。

After we rotate around the circle once, the values start repeating. Therefore, the sine curve, or “wave,” also continues to repeat. The easiest way to sketch a sine curve is to plot the points for the quadrant angles. The value of $\begin{aligned} \sin θ \end{aligned}$ goes from 0 to 1 to 0 to -1 and back to 0. Graphed along a horizontal axis, it would look like this:
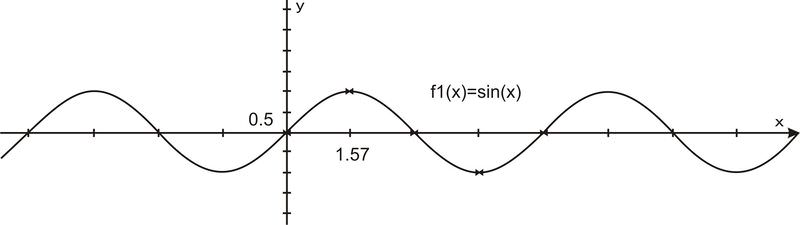
::当我们环绕圆圈旋转一次后,数值开始重复。因此,正弦曲线或“波”也继续重复。绘制正弦曲线的最简单方法是为四角绘制点。罪的值从0到1到0到1,然后又回到0。按水平轴绘制,它看起来是这样的:

Filling in the gaps in between and allowing for multiple rotations as well as negative angles results in the graph of $\begin{aligned} y = \sin x \end{aligned}$ where $\begin{aligned} x \end{aligned}$ is any angle of rotation, in radians.
::填补多个旋转和允许多个旋转之间的空白以及负角度导致 y=sinx 的图形,其中 x 是任何旋转角度, 以弧度表示。

As we have already mentioned, $\begin{aligned} \sin x \end{aligned}$ has a period of $\begin{aligned} 2 π \end{aligned}$ . You should also note that the $\begin{aligned} y - \end{aligned}$ values never go above 1 or below -1, so the range of a sine curve is $\begin{aligned} {- 1 \leq y \leq 1} \end{aligned}$ . Because angles can be any value and will continue to rotate around the circle infinitely, there is no restriction on the angle $\begin{aligned} x \end{aligned}$ , so the domain of $\begin{aligned} \sin x \end{aligned}$ is all reals.
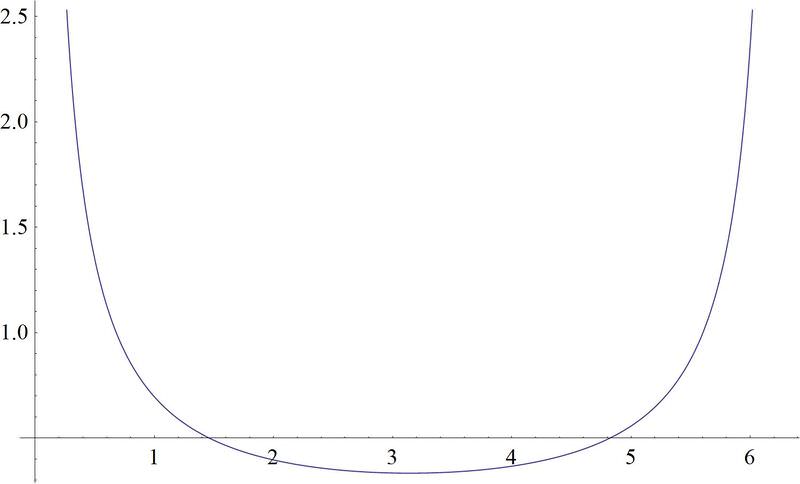
::正如我们已经提到的那样, sinx 有2。您也应该注意, y- 值从未超过 1 或低于 1-1, 所以正弦曲线的范围是 {1\\\\ y1}。因为角度可以是任何值, 并且将继续无限地围绕圆圈旋转, 角度 x 没有限制, 所以 sinx 的域是真实的。

Cosecant is the reciprocal of sine, or $\begin{aligned} \frac{1}{y} \end{aligned}$ . Therefore, whenever the sine is zero, the cosecant is going to have a vertical asymptote because it will be undefined. It also has the same sign as the sine function in the same quadrants. Here is the graph.
::Cosecant 是正弦或正弦的对等函数。因此, 当正弦为零时, 共弦就会有一个垂直的静态, 因为它是未定义的。共弦函数也具有相同的符号。这是图表。

The period of the function is $\begin{aligned} 2 π \end{aligned}$ , just like sine. The domain of the function is all real numbers, except multiples of $\begin{aligned} π {\dots - 2 π, - π, 0, π, 2 π \dots} \end{aligned}$ . The range is all real numbers greater than or equal to 1, as well as all real numbers less than or equal to -1. Notice that the range is everything except where sine is defined (other than the points at the top and bottom of the sine curve).
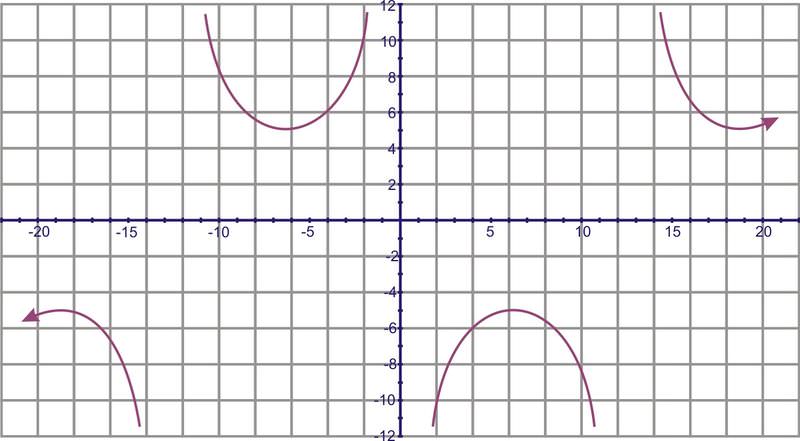
::函数的期间为 2 , 和正弦一样。函数的域是所有实际数字, 除了% ─ -2 , , , , , , , , , , , , ... } 。该范围是所有实际数字大于或等于 1 , 以及所有实际数字小于或等于-1 。请注意, 除确定正弦外( 除正弦曲线顶部和底部的点 ) , 该范围是全部区域。

Notice again the reciprocal relationships at 0 and the asymptotes. Also look at the intersection points of the graphs at 1 and -1. Many students are reminded of parabolas when they look at the half-period of the cosecant graph. While they are similar in that they each have a local minimum or maximum and they have the same beginning and ending behavior, the comparisons end there. Parabolas are not restricted by asymptotes, whereas the cosecant curve is.
::提醒注意 0 和零之间的对等关系。还要看看 1 和 - 1 的图形的交叉点。许多学生在查看 cosecant 图形的半期时会被提醒注意 parabolas 。虽然它们相似, 它们各自都有本地最低或最高限, 并且有相同的开始和结束行为 , 但比较结束于此。 Parabolas 不受 asymptotes 的限制, 而 cosecant 曲线是。

Graphing Functions
::图图函数

Graph the following functions:
::绘制以下函数图 :

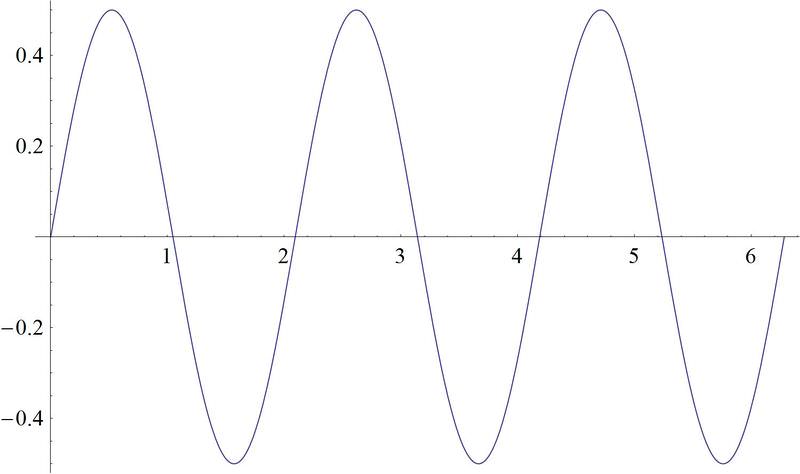
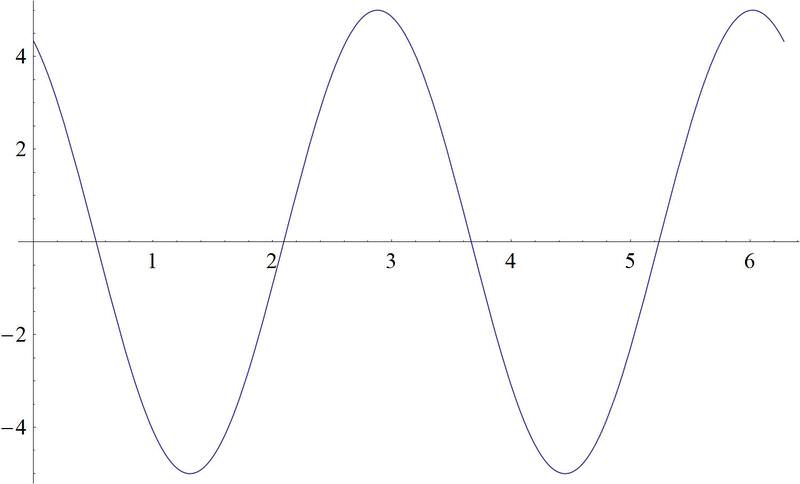
1. $\begin{aligned} g (x) = \frac{1}{2} \sin (3 x) \end{aligned}$ .
::1. g(x)=12sin(3x)

As you can see from the graph, the $\begin{aligned} \frac{1}{2} \end{aligned}$ in front of the function reduces the function's height, while the 3 inside the argument of the function makes the function "squished" along the "x" axis.
::从图中可以看到,函数前面的 12 函数会降低函数的高度, 而函数参数参数中的 3 则使函数沿着“ x” 轴“ 崩溃 ” 。

2. $\begin{aligned} f (x) = \frac{1}{3} \csc (\frac{1}{2} x) \end{aligned}$ .
::2. f(x)=13csc(12x)

3. $\begin{aligned} f (x) = 5 \sin (2 (x + \frac{π}{3})) \end{aligned}$ .
::3. f(x)=5sin(2(x)3))。

Examples
::实例

Example 1
::例1

Earlier, you were asked what pattern the shadow would trace out.
::之前有人问你影子会追踪到什么模式

As you have seen in this lesson, the shadow of a light applied vertically to a rotating clock hand would trace out a sine graph. The graph would begin at zero when the hand is lying flat along the positive "x" axis. It would then increase until the hand was vertical. It would then decrease until the rotating hand was pointing straight down. Finally, the graph would increase again to zero when the hand is returning to the positive "x" axis.
::正如你们从这个教训中看到的那样,光的阴影垂直应用到旋转时钟的手上,可以追溯一个正弦图。当手沿着正“x”轴平躺时,图将开始于零,然后会增加,直到手是垂直的。然后它会减少,直到旋转时的手正向下。最后,当手回到正“x”轴时,图将再次增加为零。

Example 2
::例2

Graph $\begin{aligned} g (x) = 5 \csc (\frac{1}{4} (x + π)) \end{aligned}$ .
::图g(x)=5csc(14(x))。

Example 3
::例3

Determine the function creating this graph:
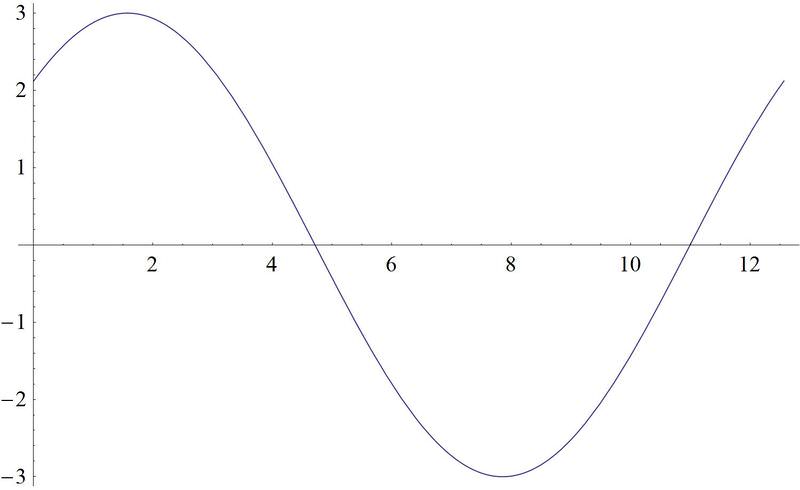
::确定创建此图的函数 :

This could be either a secant or cosecant function. We will use a cosecant model. First, the vertical shift is -1. The period is the difference between the two given $\begin{aligned} x - \end{aligned}$ values, $\begin{aligned} \frac{7 π}{4} - \frac{3 π}{4} = π \end{aligned}$ , so the frequency is $\begin{aligned} \frac{2 π}{π} = 2 \end{aligned}$ . The horizontal shift incorporates the frequency, so in $\begin{aligned} y = \csc x \end{aligned}$ the corresponding $\begin{aligned} x - \end{aligned}$ value to $\begin{aligned} (\frac{3 π}{4}, 0) \end{aligned}$ is $\begin{aligned} (\frac{π}{2}, 1) \end{aligned}$ . The difference between the $\begin{aligned} x - \end{aligned}$ values is $\begin{aligned} \frac{3 π}{4} - \frac{π}{2} = \frac{3 π}{4} - \frac{2 π}{4} = \frac{π}{4} \end{aligned}$ and then multiply it by the frequency, $\begin{aligned} 2 \cdot \frac{π}{4} = \frac{π}{2} \end{aligned}$ . The equation is $\begin{aligned} y = - 1 + \csc (2 (x - \frac{π}{2})) \end{aligned}$ .
::可以是偏移函数, 也可以是 cosecant 函数。我们将使用 cosecant 模型。首先, 垂直转换为 - 1. 时间段是给定的 x- 值之间的差值, 74 - 34 4 4 , 所以频率是 22 。水平转换包含频率, 所以在 y= cscx 中, 相应的 x- 值 (34, 0) 是 (%2, 2) 。 x- 值之间的差值是 34 2= 34 - 24 4, 然后乘以频率 24 2 。方程式是 y1+ csc ( 2x) 。

Example 4
::例4

Graph $\begin{aligned} h (x) = 3 \sin (\frac{1}{2} (x + \frac{π}{2})) \end{aligned}$ .
::图h(x)=3sin(12(x)2)。

Review
::回顾

Graph each of the following functions.
::绘制下列函数的每一个图。

$\begin{aligned} f (x) = \sin (x) \end{aligned}$ .
:xx) =sin(x) 。

$\begin{aligned} h (x) = \sin (2 x) \end{aligned}$ .
::h(x) =sin(2x) 。

$\begin{aligned} k (x) = \sin (2 x + π) \end{aligned}$ .
: kx) =sin( 2x) 。

$\begin{aligned} m (x) = 2 \sin (2 x + π) \end{aligned}$ .
:x) = 2sin(2x) 。

$\begin{aligned} g (x) = 2 \sin (2 x + π) + 2 \end{aligned}$ .
::g(x) = 2sin @ (2x) +2 。

$\begin{aligned} f (x) = \csc (x) \end{aligned}$ .
:fx) = csc(x) 。

$\begin{aligned} h (x) = \csc (2 x) \end{aligned}$ .
::h(x) = csc(2x) 。

$\begin{aligned} k (x) = \csc (2 x + π) \end{aligned}$ .
: kx) = csc( 2x) 。

$\begin{aligned} m (x) = 2 \csc (2 x + π) \end{aligned}$ .
:x)=2csc(2x)

$\begin{aligned} g (x) = 2 \csc (2 x + π) + 2 \end{aligned}$ .
::g(x)=2csc(2x)+2。

$\begin{aligned} h (x) = \sin (3 x) \end{aligned}$ .
::h(x) =sin(3x) 。

$\begin{aligned} k (x) = \sin (3 x + \frac{π}{2}) \end{aligned}$ .
: kx) =sin( 3x2) 。

$\begin{aligned} m (x) = 3 \sin (3 x + \frac{π}{2}) \end{aligned}$ .
:x)=3sin(3x)2。

$\begin{aligned} g (x) = 3 \sin (3 x + \frac{π}{2}) + 3 \end{aligned}$ .
::g(x) = 3sin(3x2)+3。

$\begin{aligned} h (x) = \csc (3 x) \end{aligned}$ .
::h(x) = csc(3x) 。

$\begin{aligned} k (x) = \csc (3 x + \frac{3 π}{2}) \end{aligned}$ .
:xx) = csc(3x+32)。

$\begin{aligned} m (x) = 4 \csc (3 x + \frac{3 π}{2}) \end{aligned}$ .
:x)=4csc(3x+32)。

$\begin{aligned} g (x) = 4 \csc (3 x + \frac{3 π}{2}) - 3 \end{aligned}$ .
::g(x)=4csc(3x+32)-3。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

Sine 和 Cosescant 图形

Sine and Cosecant Graphs ::Sine 和 Cosescant 图形

Graphing Functions ::图图函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Sine and Cosecant Graphs
::Sine 和 Cosescant 图形

Graphing Functions
::图图函数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)