2.10 脊椎和清扫图

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 余弦和清扫图

  Collapse Expand

  余弦和清扫图

  播放段落

  Imagine for a moment that you have a clock that has only one hand - that rotates counterclockwise!. However, the hand is very slim all the way until the tip, where there is a ball on the end. In fact, the hand is so slim you won't notice it. You only notice the ball on the end of the rotating hand. This hand is rotating faster than normal.
  ::想象一下, 你有一个只有一只手的时钟—— 即逆时旋转! 但是, 手会一直很瘦, 直到尖端, 上面有一个球。 事实上, 手是如此的瘦, 您不会注意到它。 您只注意到旋转手的尾端的球。 此手的旋转速度比正常的要快 。

  

  播放段落

  Consider what it would be like if you put a light above the clock and let the shadow of the hands fall on the wall under the clock. What pattern would that shadow trace out? If you think about it, you might realize that the shadow would make an left and right motion, over and over as the hand of the clock rotated. Now imagine that instead of a wall, there was a large piece of paper for the shadow to fall on. And wherever the shadow fell, there would be a mark on the paper. Finally, imagine moving the paper as the clock rotates. Can you imagine sort of pattern this would trace out?
  ::想象一下,如果你把光照在时钟上方,让手的影子在时钟下落在墙上,那会是什么样子。那个影子会追溯到什么模式?如果你想到它,你可能会意识到,当时钟旋转时,阴影会向左和向右移动。现在想象一下,不是墙,阴影会掉落,而是有一大块纸。不管影子掉落到哪里,纸上都会有一个标记。最后,想象一下,当时钟旋转时,纸会移动。你能想象出这样可以追溯的模式吗?

  播放段落

  Cosine and Secant Graphs
  ::余弦和清扫图

  播放段落

  If you have read other Trigonometry sections in this course, you may have learned that are very closely related. The cosine of an angle is the same as the sine of its complementary angle. So, it should not be a surprise that sine and cosine waves are very similar in that they are both periodic with a period of $\begin{align*}2\pi\end{align*}$ , a range from -1 to 1, and a domain of all real angles.
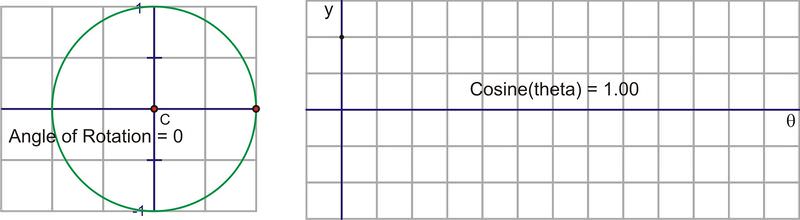
  ::如果您读过这门课中的其他三角测量部分, 您可能已经学到了非常密切关联的部分。 一个角度的余弦与其互补角度的正弦相同。 因此, 弦和弦波非常相似并不令人惊讶, 因为两者的周期性是2°, 从-1到1°, 以及所有实际角度的域 。

  播放段落

  The cosine of an angle is the ratio of $\begin{align*}\frac{x}{r}\end{align*}$ , so in the unit circle , the cosine is the $\begin{align*}x-\end{align*}$ coordinate of the point of rotation. If we trace the $\begin{align*}x-\end{align*}$ coordinate through a rotation, notice the change in the distance of $\begin{align*}\cos x\end{align*}$ starts at one. The $\begin{align*}x-\end{align*}$ coordinate at $\begin{align*}0^\circ\end{align*}$ is 1 and the $\begin{align*}x-\end{align*}$ coordinate for $\begin{align*}90^\circ\end{align*}$ is 0, so the cosine value is decreasing from 1 to 0 through the $\begin{align*}1^{st}\end{align*}$ quadrant.
  ::角的余弦是 xr 之比, 所以在单位圆中, 余弦是旋转点的 x - 坐标。 如果我们通过旋转追踪 x - 坐标, 注意COsx从一时开始的距离变化 。 0 ° 的 x - 坐标为 1 , 90 ° 的 x - 坐标为 0 , 因此共弦值从 1 到 0 到 1 象限 。

  

  

  

  

  播放段落

  Here is a sequence of rotations. Compare the $\begin{align*}x-\end{align*}$ coordinate of the point of rotation with the height of the point as it traces along the horizontal. These pictures plot $\begin{align*}(\theta, \cos \theta)\end{align*}$ on the coordinate plane as $\begin{align*}(x, y)\end{align*}$ .
  ::下面是旋转的顺序。 比较旋转点的 x - 坐标和点沿水平的高度。 这些坐标平面上的图片图( , cos) 以 (x,y) 表示 。

  

  

  

  

  

  播放段落

  Plotting the quadrant angles and filling in the in-between values shows the graph of $\begin{align*}y = \cos x\end{align*}$
  ::绘制象形角度和填充介于数值之间的值时显示 y=cosx 的图形

  

  

  播放段落

  The graph of $\begin{align*}y = \cos x\end{align*}$ has a period of $\begin{align*}2\pi\end{align*}$ . The range of a cosine curve is $\begin{align*}\left \{-1 \le y \le 1 \right \}\end{align*}$ and the domain of $\begin{align*}\cos x\end{align*}$ is all reals. If you've studied the sine function, you may notice that the shape of the curve is exactly the same, but shifted by $\begin{align*}\frac{\pi}{2}\end{align*}$ .
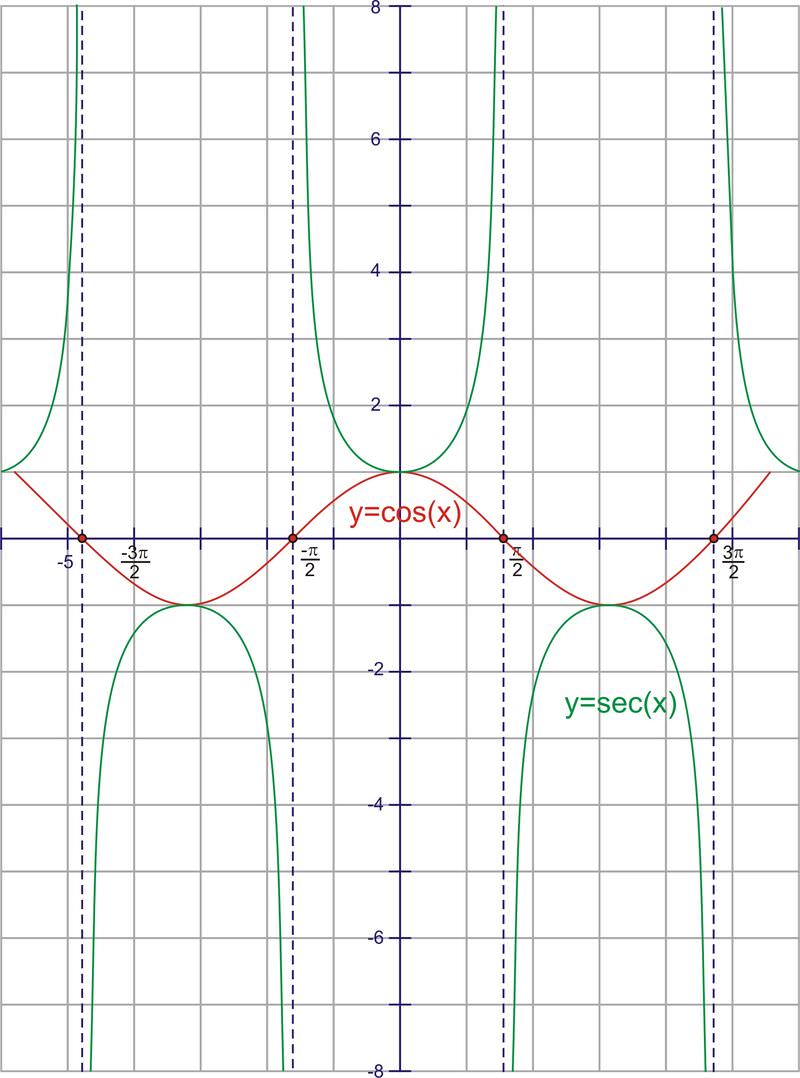
  ::y=cosx 的图形有2°Q的时段。 余弦曲线的范围是\\\\\\\\\y\\\1} , 共弦曲线的域是真实的。 如果您研究了正弦函数, 您可以注意到曲线的形状完全相同, 但被 \\\\ 2 移动了 。

  播放段落

  Secant is the reciprocal of cosine, or $\begin{align*}\frac{1}{x}\end{align*}$ . Therefore, whenever the cosine is zero, the secant is going to have a vertical asymptote because it will be undefined. It also has the same sign as the cosine function in the same quadrants. Here is the graph.
  ::secant 是 cosine 或 1x 的对等 。 因此, 当 cosine 是 零 时, secant 将会有一个垂直的静态, 因为它是未定义的 。 它也具有与 相同 夸度 的 cosine 函数相同的符号 。 以下是图表 。

  

  播放段落

  The period of the function is $\begin{align*}2\pi\end{align*}$ , just like cosine. The domain of the function is all real numbers, except multiples of $\begin{align*}\pi\end{align*}$ starting at $\begin{align*}\frac{\pi}{2}. \left \{ \ldots \frac{-\pi}{2}, \frac{\pi}{2}, 0, \frac{3\pi}{2}, \frac{5\pi}{2} \ldots \right \}\end{align*}$ . The range is all real numbers greater than or equal to 1 as well as all real numbers less than or equal to -1. Notice that the range is everything except where cosine is defined (other than the tops and bottoms of the cosine curve).
  ::函数的周期为 2 , 和 余弦一样。 函数的域是所有真实数字, 除了% 2 {...\\\\\\\\\\\\\\\\\\\\\\\\\\2, 0,3\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  

  播放段落

  Notice again the reciprocal relationships at 0 and the asymptotes. Also look at the intersection points of the graphs at 1 and -1. Again, this graph looks parabolic, but it is not.
  ::再次注意 0 的对等关系和 asymptotes 。 还要查看 1 和 - 1 的图形的交叉点 。 另外, 此图表看起来是抛物线, 但并非如此 。

  播放段落

  Sketch the graph
  ::绘制图形

  播放段落

  Sketch a graph of $\begin{align*}h(x)=5+\frac{1}{2} \sec 4x\end{align*}$ over the interval $\begin{align*}[0, 2\pi]\end{align*}$ .
  ::在间隔[0,2]内绘制 h(x)=5+12sec4x的图。

  播放段落

  If you compare this example to $\begin{align*}f(x)=\sec x\end{align*}$ , it will be translated 5 units up, with an of $\begin{align*}\frac{1}{2}\end{align*}$ and a frequency of 4. This means in our interval of 0 to $\begin{align*}2\pi\end{align*}$ , there will be 4 secant curves.
  ::如果您将该示例比作 f( x) =secx, 它将被翻译为 5 个单位向上, 12 个单位向上, 频率为 4 个单位向上 。 这意味着在 0 到 2 之间, 将会有 4 秒曲线 。

  

  播放段落

  Find the equation for the graph below.
  ::查找下图的方程式 。

  

  播放段落

  First of all, this could be either a secant or cosecant function. Let’s say this is a secant function. Secant usually intersects the $\begin{align*}y-\end{align*}$ axis at $\begin{align*}(0, 1)\end{align*}$ at a minimum. Now, that corresponding minimum is $\begin{align*}\left(\frac{\pi}{2}, -2\right)\end{align*}$ . Because there is no amplitude change, we can say that the vertical shift is the difference between the two $\begin{align*}y-\end{align*}$ values, -3. It looks like there is a phase shift and a period change. From minimum to minimum is one period, which is $\begin{align*}\frac{9\pi}{2}-\frac{\pi}{2}=\frac{8\pi}{2}=4\pi\end{align*}$ and $\begin{align*}B=\frac{2\pi}{4\pi}=\frac{1}{2}\end{align*}$ . Lastly, we need to find the horizontal shift. Since secant usually intersects the $\begin{align*}y-\end{align*}$ axis at $\begin{align*}(0, 1)\end{align*}$ at a minimum, and now the corresponding minimum is $\begin{align*}\left(\frac{\pi}{2}, -2\right)\end{align*}$ , we can say that the horizontal shift is the difference between the two $\begin{align*}x-\end{align*}$ values, $\begin{align*}\frac{\pi}{2}\end{align*}$ . Therefore, our equation is $\begin{align*}f(x)=-3+ \sec \left(\frac{1}{2}(x-\frac{\pi}{2} \right))\end{align*}$ .
  ::首先,这可以是偏移函数,也可以是 cosecant 函数。 可以说这是一个偏移函数。 secant 通常在最小值( 0, 1) 时将 y - oxis 交叉。 现在, 相应的最小值是 (2, - 2) 。 因为没有振幅变化, 我们可以说垂直变化是两个 y - 值之间的差别, - 3 。 它看起来像是一个阶段变化和一个时期的变化。 从最小值到最小值为 一个时期, 即 92 2= 82= 4 和 B= 24 12。 最后, 我们需要找到水平变化 。 因为 偏移通常在最小值( 0, 1) 时将 y - oxis 交叉开, 而现在相应的最小值是 (2) 。 我们可以说, 水平变化是两个 x - 值之间的差别 。 2。 因此, 我们的方程式是 f (x) 3+sec ( 12 (x) 2) 。

  播放段落

  Graph the function $\begin{align*}h(x)=2 - 3 \cos 4x\end{align*}$
  ::函数 h( x) =2 - 3cos4x

  

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked what would the shadow trace out. 
  ::之前有人问你 影子会追踪到什么

  播放段落

  As you have learned in this section, a light shining down on the rotating hand would create a shadow in the pattern of a cosine function, starting at a maximum value as the hand is lying along the "x" axis, going through zero to a maximum negative value when the hand is lying along the negative "y" axis. It would then begin to increase until it returned to a maximum value when the rotating hand was again lying along the positive "x" axis.
  ::正如您在本节中所学到的, 旋转手上的光照下, 会在余弦函数模式中产生阴影, 开始于最大值, 因为手正躺在“ x” 轴上, 穿过零到最大负值, 当手躺在负“ y” 轴上。 然后它开始增加, 直到旋转手又躺在正“ x” 轴上, 返回到最大值 。

  播放段落

  Example 2
  ::例2

  播放段落

  Graph $\begin{align*}y=-2+\frac{1}{2} \sec(4(x-1))\end{align*}$ .
  ::图y2+12sec(4(x-1)).

  

  播放段落

  Example 3
  ::例3

  播放段落

  Determine the function creating this graph:
  ::确定创建此图的函数 :

  

   

  播放段落

  This could be either a secant or cosecant function. We will use a cosecant model. First, the vertical shift is -1. The period is the difference between the two given $\begin{align*}x-\end{align*}$ values, $\begin{align*}\frac{7\pi}{4}-\frac{3\pi}{4}=\pi\end{align*}$ , so the frequency is $\begin{align*}\frac{2\pi}{\pi}=2\end{align*}$ . The horizontal shift incorporates the frequency, so in $\begin{align*}y=\csc x\end{align*}$ the corresponding $\begin{align*}x-\end{align*}$ value to $\begin{align*}\left(\frac{3\pi}{4}, 0\right)\end{align*}$ is $\begin{align*}\left(\frac{\pi}{2}, 1\right)\end{align*}$ . The difference between the $\begin{align*}x-\end{align*}$ values is $\begin{align*}\frac{3\pi}{4}-\frac{\pi}{2}=\frac{3\pi}{4}-\frac{2\pi}{4}=\frac{\pi}{4}\end{align*}$ and then multiply it by the frequency, $\begin{align*}2 \cdot \frac{\pi}{4}=\frac{\pi}{2}\end{align*}$ . The equation is $\begin{align*}y=-1+ \csc \left(2(x-\frac{\pi}{2}\right))\end{align*}$ .
  ::可以是偏移函数, 也可以是 cosecant 函数 。 我们将使用 cosecant 模型。 首先, 垂直转换为 - 1. 时间段是给定的 x- 值之间的差值, 74 - 34 4 4 , 频率为 22 。 水平转换包含频率, 所以在 y= cscx 中, 相应的 x- 值为 (34, 0) (%2) 。 x- 值之间的差值是 34 2 = 34 - 24 4 4 4, 乘以频率 24 2 。 方程式是 y1+ csc (2( x2 ) 。

  播放段落

  Example 4
  ::例4

  播放段落

  Graph $\begin{align*}h(x)=\frac{1}{3} \cos 2x\end{align*}$
  ::图h(x)=13cos2x

  

  播放段落

  Review
  ::回顾

  播放段落

  Graph each of the following functions.
  ::绘制下列函数的每一个图。

  播放段落
  1. $\begin{align*}f(x)=\cos(x)\end{align*}$ .
     :x) =cos(x) 。
  播放段落
  2. $\begin{align*}h(x)=\cos(2x)\end{align*}$ .
     ::h(x) = cos( 2x) 。
  播放段落
  3. $\begin{align*}k(x)=\cos(2x+\pi)\end{align*}$ .
     :kx) = cos( 2x) 。
  播放段落
  4. $\begin{align*}m(x)=-2\cos(2x+\pi)\end{align*}$ .
     :x)%%%2cos(2x%) 。
  播放段落
  5. $\begin{align*}g(x)=-2\cos(2x+\pi)+1\end{align*}$ .
     ::g(x) 2cos( 2x) +1 。
  播放段落
  6. $\begin{align*}f(x)=\sec(x)\end{align*}$ .
     :fx) =sec(x) 。
  播放段落
  7. $\begin{align*}h(x)=\sec(3x)\end{align*}$ .
     ::h(x) =sec(3x) 。
  播放段落
  8. $\begin{align*}k(x)=\sec(3x+\pi)\end{align*}$ .
     : kx) =sec( 3x) 。
  播放段落
  9. $\begin{align*}m(x)=2\sec(3x+\pi)\end{align*}$ .
     :x)=2sec(3x)
  播放段落
  10. $\begin{align*}g(x)=3+2\sec(3x+\pi)\end{align*}$ .
      ::g(x) =3+2sec(3x) 。
  播放段落
  11. $\begin{align*}h(x)=\cos(\frac{x}{2})\end{align*}$ .
      ::h(x) = cos(x2) 。
  播放段落
  12. $\begin{align*}k(x)=\cos(\frac{x}{2}+\frac{\pi}{2})\end{align*}$ .
      :kx) = cos(x2\% 2) 。
  播放段落
  13. $\begin{align*}m(x)=2\cos(\frac{x}{2}+\frac{\pi}{2})\end{align*}$ .
      :x) = 2cos(x2) = 2。
  播放段落
  14. $\begin{align*}g(x)=2\cos(\frac{x}{2}+\frac{\pi}{2})-3\end{align*}$ .
      ::g(x) = 2cos(x22) - 3。
  播放段落
  15. $\begin{align*}h(x)=\sec(\frac{x}{4})\end{align*}$ .
      ::h(x) =sec(x4) 。
  播放段落
  16. $\begin{align*}k(x)=\sec(\frac{x}{4}+\frac{3\pi}{2})\end{align*}$ .
      :xx) = sec(x4+3) 。
  播放段落
  17. $\begin{align*}m(x)=-3\sec(\frac{x}{4}+\frac{3\pi}{2})\end{align*}$ .
      :x)%3sec(x4+3)2。
  播放段落
  18. $\begin{align*}g(x)=2-3\sec(\frac{x}{4}+\frac{3\pi}{2})\end{align*}$ .
      ::g(x) =2- 3sec(x4+32)。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。