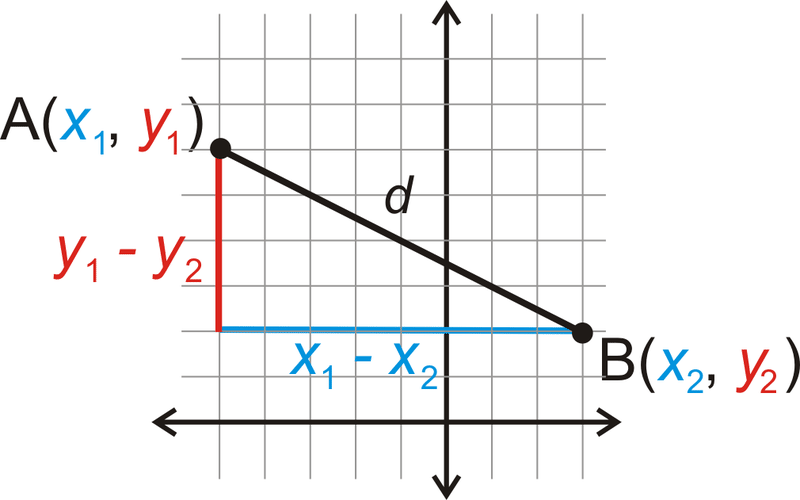Course: 8.3 毕达哥里安神论的应用

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 毕达哥里安神论应用

Collapse Expand
毕达哥里安神论应用
Applications of the Pythagorean Theorem
::毕达哥里安神论应用

Find the Height of an Isosceles Triangle
::查找 Isosceles 三角的高度

One way to use The Pythagorean Theorem is to find the height of an isosceles triangle (see Example 1).
::使用Pytagorean定理的一个方法就是找到等分形三角形的高度(见例1)。

Prove the Distance Formula
::证明距离公式

Another application of the Pythagorean Theorem is the Distance Formula. We will prove it here.
::Pytagoren定理的另一个应用是距离公式。我们将在这里证明它。

Let’s start with point $\begin{aligned} A (x_{1}, y_{1}) \end{aligned}$ and point $\begin{aligned} B (x_{2}, y_{2}) \end{aligned}$ . We will call the distance between $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B, d \end{aligned}$ .
::我们先从A(x1,y1)点和B(x2,y2)点开始,然后调用A与B(d)之间的距离。

Draw the vertical and horizontal lengths to make a right triangle .
::绘制垂直和水平长度以建立右三角形。

Now that we have a right triangle, we can use the Pythagorean Theorem to find the hypotenuse , $\begin{aligned} d \end{aligned}$ .
::现在我们有一个正确的三角形, 我们可以利用毕达哥里安神话来找到下限, d.

$\begin{aligned} d^{2} & = (x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2} \\ d & = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}} \end{aligned}$

::d2=(x1-x2)2+(y1-y2)2+(y1-y2)2d=(x1-x2)2+(y1-y2)2+2

Distance Formula: The distance between $\begin{aligned} A (x_{1}, y_{1}) \end{aligned}$ and $\begin{aligned} B (x_{2}, y_{2}) \end{aligned}$ is $\begin{aligned} d = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}} \end{aligned}$ .
::距离公式: A( x1,y1) 和 B( x2,y2) 之间的距离是 d= (x1 - x2) 2+ (y1 -y2) 。

Classify a Triangle as Acute, Right, or Obtuse
::三角形分类为急性、右或阻塞

We can extend the to determine if a triangle is an obtuse or acute triangle .
::我们可以扩展三角形,以确定三角形是隐形还是尖形三角形。

Acute Triangles: If the sum of the squares of the two shorter sides in a right triangle is greater than the square of the longest side, then the triangle is acute.
::急性三角形:如果右三角形中两个较短边的平方大于最长边的平方,则三角形为急性。

For $\begin{aligned} b < c \end{aligned}$ and $\begin{aligned} a < c \end{aligned}$ , if $\begin{aligned} a^{2} + b^{2} > c^{2} \end{aligned}$ , then the triangle is acute.
::b<c 和 a<c, 如果 a2+b2>c2, 那么三角形是急性的。

Obtuse Triangles: If the sum of the squares of the two shorter sides in a right triangle is less than the square of the longest side, then the triangle is obtuse.
::障碍三角:如果右三角形中两边短方的平方和小于最长边的平方,则三角形是模糊的。

For $\begin{aligned} b < c \end{aligned}$ and $\begin{aligned} a < c \end{aligned}$ , if $\begin{aligned} a^{2} + b^{2} < c^{2} \end{aligned}$ , then the triangle is obtuse.
::b<c 和 a<c, 如果 a2+b2 < c2, 那么三角形是模糊的。

What if you were given an in which all the sides measured 4 inches? How could you use the Pythagorean Theorem to find the triangle's ?
::假若你们获得一个四公分宽四英寸的柱子,你们怎能用毕达哥伦定理仪找到三角形呢?

Examples
::实例

Example 1
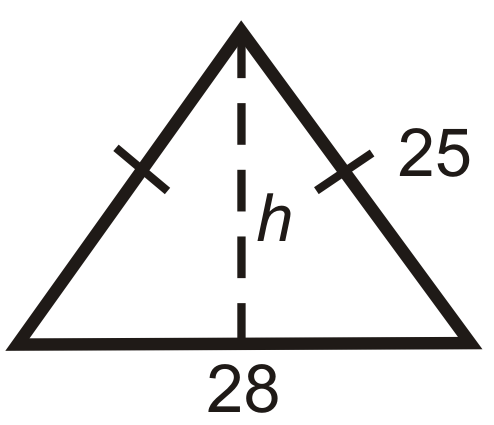
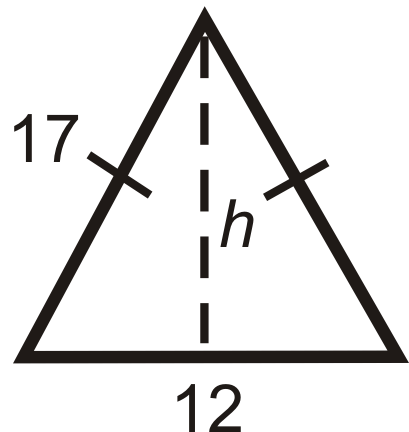
::例1

What is the height of the isosceles triangle?
::等分形三角形的高度是多少?

Draw the altitude from the vertex between the congruent sides, which will bisect the base.
::从相近两侧的顶端中绘制高度,使底部两分。

$\begin{aligned} 7^{2} + h^{2} & = 9^{2} \\ 49 + h^{2} & = 81 \\ h^{2} & = 32 \\ h & = \sqrt{32} = \sqrt{16 \cdot 2} = 4 \sqrt{2} \end{aligned}$

::72+h2=9249+h2=81h2=32h=32=16_2=42

Example 2
::例2

Find the distance between (1, 5) and (5, 2).
::查找(1,5)和(5,2)之间的距离。

Make $\begin{aligned} A (1, 5) \end{aligned}$ and $\begin{aligned} B (5, 2) \end{aligned}$ . Plug into the distance formula.
::Make A( 1, 5) 和 B( 5, 2) 。插入距离公式。

$\begin{aligned} d & = \sqrt{(1 - 5)^{2} + (5 - 2)^{2}} \\ = \sqrt{(- 4)^{2} + (3)^{2}} \\ = \sqrt{16 + 9} = \sqrt{25} = 5 \end{aligned}$

::d=(1-5)2+(5-2)2=(-4)2+(3)2=16+9=25=5

Just like the lengths of the sides of a triangle, distances are always positive.
::就像三角形两边的长度一样距离总是正数

Example 3
::例3

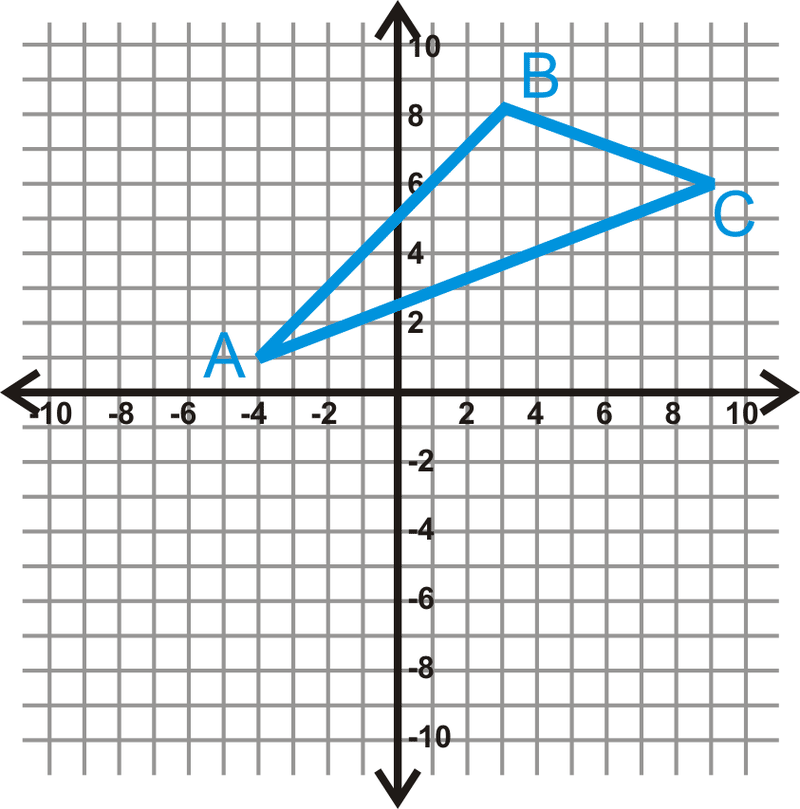
Graph $\begin{aligned} A (- 4, 1), B (3, 8) \end{aligned}$ , and $\begin{aligned} C (9, 6) \end{aligned}$ . Determine if $\begin{aligned} △ A B C \end{aligned}$ is acute, obtuse, or right.
::图A(-4,1),B(3,8)和C(9,6),确定ABC是急性、延迟或右。

Use the distance formula to find the length of each side.
::使用距离公式查找每侧的长度。

$\begin{aligned} A B & = \sqrt{(- 4 - 3)^{2} + (1 - 8)^{2}} = \sqrt{49 + 49} = \sqrt{98} \\ B C & = \sqrt{(3 - 9)^{2} + (8 - 6)^{2}} = \sqrt{36 + 4} = \sqrt{40} \\ A C & = \sqrt{(- 4 - 9)^{2} + (1 - 6)^{2}} = \sqrt{169 + 25} = \sqrt{194} \end{aligned}$

::AB=(-4-3)2+(1-8)2+(1-8)2=49+49=98BC=(3-9)2+(8-6)2=36+4=40AC=(-4-9)2+(1-6)2=169+25=194

Plug these lengths into the Pythagorean Theorem.
::把这些长度插进毕达哥里安神话

$\begin{aligned} {(\sqrt{98})}^{2} + {(\sqrt{40})}^{2} & ? {(\sqrt{194})}^{2} \\ 98 + 40 & ? 194 \\ 138 & < 194 \end{aligned}$

$\begin{aligned} △ A B C \end{aligned}$ is an obtuse triangle .
::ABC是一个隐形三角形。

For Examples 4 and 5, determine if the triangles are acute, right or obtuse.
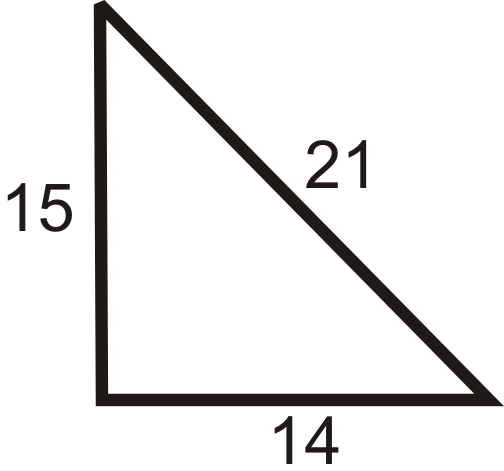
::对于例4和例5,确定三角形是尖尖的、右的还是斜的。

Example 4
::例4

Set the longest side to $\begin{aligned} c \end{aligned}$ .
::将最长的边设为 c 。

$\begin{aligned} 15^{2} + 14^{2} & ? 21^{2} \\ 225 + 196 & ? 441 \\ 421 & < 441 \end{aligned}$

The triangle is obtuse.
::三角形是模糊的。

Example 5
::例5

Set the longest side to $\begin{aligned} c \end{aligned}$ .
::将最长的边设为 c 。

A triangle with side lengths 5, 12, 13.
::侧长5,12,13的三角形

$\begin{aligned} 5^{2} + 12^{2} = 13^{2} \end{aligned}$ so this triangle is right.
::52+122=132 所以三角形是对的

Review
::回顾

Find the height of each isosceles triangle below. Simplify all radicals.
::查找下方每个等分三角形的高度。简化所有基体。

Find the length between each pair of points.
::查找每对点之间的长度。

(-1, 6) and (7, 2)
:-1,6)和(7,2)

(10, -3) and (-12, -6)
:10,3)和(12,6)

(1, 3) and (-8, 16)
:第1款、第3款)和(第8条、第16条)

Standard definition TVs have a length and width ratio of 4:3. What are the length and width of a 42” Standard definition TV? Round your answer to the nearest tenth.
::标准定义电视的长度和宽度比例为4:3,42“标准定义电视”的长度和宽度是多少?

Determine whether the following triangles are acute, right or obtuse.
::确定以下三角形是尖锐的、右的还是隐蔽的。

7, 8, 9

14, 48, 50

5, 12, 15

13, 84, 85

20, 20, 24

35, 40, 51

39, 80, 89

20, 21, 38

48, 55, 76

Graph each set of points and determine whether $\begin{aligned} △ A B C \end{aligned}$ is acute, right, or obtuse, using the distance formula.
::使用距离公式, 绘制每组点数的图, 并确定 ABC 是急性、右、或斜度。

$\begin{aligned} A (3, - 5), B (- 5, - 8), C (- 2, 7) \end{aligned}$
::A(3,-5),B(-5,-8),C(-2,7)

$\begin{aligned} A (5, 3), B (2, - 7), C (- 1, 5) \end{aligned}$
::A(5,3),B(2,-7),C(-1,5)

$\begin{aligned} A (1, 6), B (5, 2), C (- 2, 3) \end{aligned}$
::A(1,6,B(5,5,5),C(-2,3)

$\begin{aligned} A (- 6, 1), B (- 4, - 5), C (5, - 2) \end{aligned}$
::A(6)1,B(-4)-5,C(5)-2,A(6)1,B(-4)-5,C(5)-2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

Section outline

General

毕达哥里安神论应用

Applications of the Pythagorean Theorem ::毕达哥里安神论应用

Find the Height of an Isosceles Triangle ::查找 Isosceles 三角的高度

Prove the Distance Formula ::证明距离公式

Classify a Triangle as Acute, Right, or Obtuse ::三角形分类为急性、右或阻塞

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Applications of the Pythagorean Theorem
::毕达哥里安神论应用

Find the Height of an Isosceles Triangle
::查找 Isosceles 三角的高度

Prove the Distance Formula
::证明距离公式

Classify a Triangle as Acute, Right, or Obtuse
::三角形分类为急性、右或阻塞

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源