Course: 8.4 类似三角 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

类似三角形

Inscribed Similar Triangles Theorem
::类似三角类似定理

Remember that if two objects are similar , their are congruent and their sides are proportional in length. The of a right triangle creates similar triangles .
::记住,如果两个对象相似,它们是相近的,两边的长度是成比例的。右三角形创建相似的三角形。

Inscribed Similar Triangles Theorem : If an altitude is drawn from the right angle of any right triangle, then the two triangles formed are similar to the original triangle and all three triangles are similar to each other.
::类似三角形的定理:如果从右三角形的右角引出一个高度,则形成的两个三角形与原来的三角形相似,所有三个三角形都相似。

In $\begin{align*}\triangle ADB, m \angle A = 90^{\circ}\end{align*}$ and $\begin{align*}\overline{AC} \bot \overline{DB}\end{align*}$ :
::在亚行,mA=90 和AC=DB:

So, $\begin{align*}\triangle ADB \sim \triangle CDA \sim \triangle CAB\end{align*}$ :
::那么,亚历山德拉・卡巴:

This means that all of the corresponding sides are proportional. You can use this fact to find missing lengths in right triangles.
::这意味着所有对应的侧面都是比例的。您可以使用这个事实在右三角形中找到缺失的长度。

What if you drew a line from the right angle of a right triangle perpendicular to the side that is opposite that angle ? How could you determine the length of that line?
::如果您从右三角形右角直直到对面的侧边划线, 如何确定该直线的长度 ?

Examples
::实例

Example 1
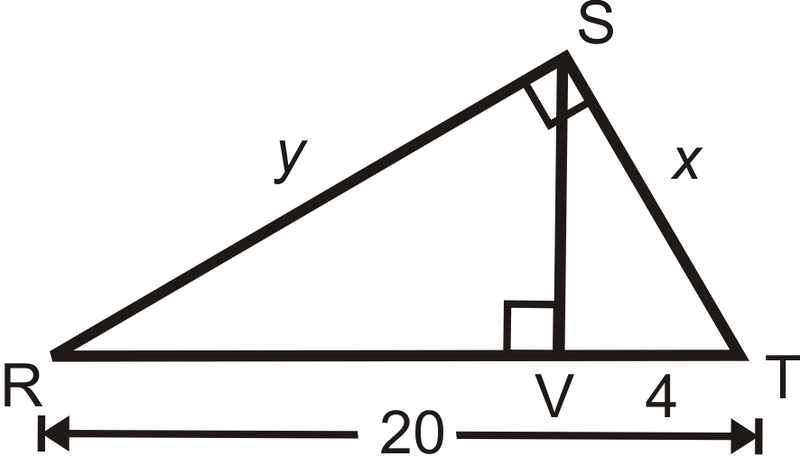
::例1

Find the value of $\begin{align*}x\end{align*}$ .
::查找 x 的值。

Set up a proportion .
::定一个比例。

\begin{aligned} \frac{shorter leg in △ S V T}{shorter leg in △ R S T} & = \frac{hypotenuse in △ S V T}{hypotenuse in △ R S T} \\ \frac{4}{x} & = \frac{x}{20} \\ x^{2} & = 80 \\ x & = \sqrt{80} = 4 \sqrt{5} \end{aligned}

$\begin{align*}\frac{\text{shorter leg in} \ \triangle SVT}{\text{shorter leg in} \ \triangle RST} &= \frac{\text{hypotenuse in} \ \triangle SVT}{\text{hypotenuse in} \ \triangle RST}\\ \frac{4}{x} &= \frac{x}{20}\\ x^2 &= 80\\ x &= \sqrt{80} = 4 \sqrt{5}\end{align*}$
::在\\\RST=hypotenuse \\\\\\\RST4x=x20x2=80x=80=45 \\\\\SVThypotenuse\\\\\SVThypotenuse\\\\\\SVT\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x20x2=80x=80x=80x=80=45\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Example 2
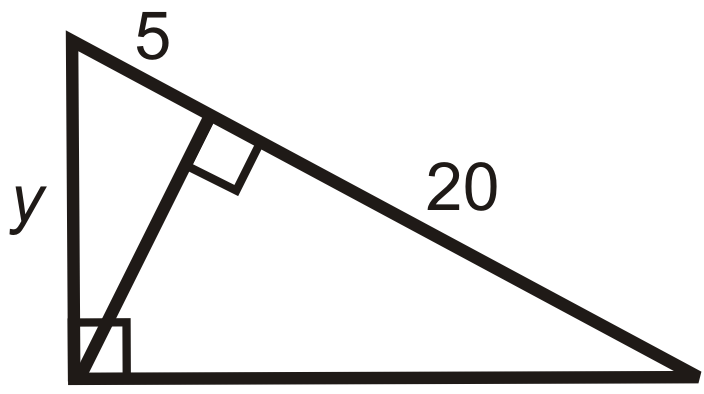
::例2

Now find the value of $\begin{align*}y\end{align*}$ in $\begin{align*}\triangle RST\end{align*}$ above.
::现在在上面的 RST 中查找 y 值。

Use the Pythagorean Theorem .
::使用毕达哥里神话

\begin{aligned} y^{2} + {(4 \sqrt{5})}^{2} & = 20^{2} \\ y^{2} + 80 & = 400 \\ y^{2} & = 320 \\ y & = \sqrt{320} = 8 \sqrt{5} \end{aligned}

$\begin{align*}y^2 + \left( 4 \sqrt{5} \right )^2 &= 20^2\\ y^2 + 80 &= 400\\ y^2 &= 320\\ y &= \sqrt{320} = 8 \sqrt{5}\end{align*}$
::y2+(452)=202y2+80=40000y2=320y=320=85

Example 3
::例3

Find the value of $\begin{align*}x\end{align*}$ .
::查找 x 的值。

Separate the triangles to find the corresponding sides.
::将三角形分隔开以找到对应的边。

Set up a proportion.
::定一个比例。

\begin{aligned} \frac{shorter leg in △ E D G}{shorter leg in △ D F G} & = \frac{hypotenuse in △ E D G}{hypotenuse in △ D F G} \\ \frac{6}{x} & = \frac{10}{8} \\ 48 & = 10 x \\ 4.8 & = x \end{aligned}

$\begin{align*}\frac{\text{shorter leg in} \ \triangle EDG}{\text{shorter leg in} \ \triangle DFG} &= \frac{\text{hypotenuse in} \ \triangle EDG}{\text{hypotenuse in} \ \triangle DFG}\\ \frac{6}{x} &= \frac{10}{8}\\ 48 &= 10x\\ 4.8 &= x\end{align*}$
::DFG=Hypotenuse DFG6x=10848=10x4.8=x

Example 4
::例4

Find the value of $\begin{align*}x\end{align*}$ .
::查找 x 的值。

Set up a proportion.
::定一个比例。

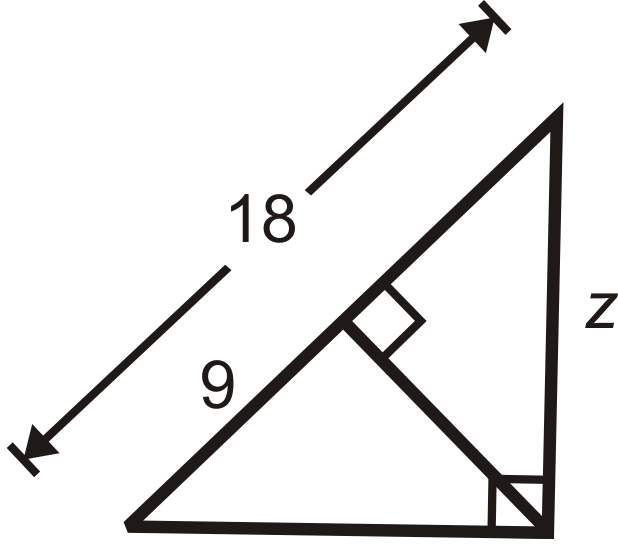
\begin{aligned} \frac{s h o r t e r l e g o f s m a l l e s t △}{s h o r t e r l e g o f m i d d l e △} & = \frac{l o n g e r l e g o f s m a l l e s t △}{l o n g e r l e g o f m i d d l e △} \\ \frac{9}{x} & = \frac{x}{27} \\ x^{2} & = 243 \\ x & = \sqrt{243} = 9 \sqrt{3} \end{aligned}

$\begin{align*}\frac{shorter \ leg \ of \ smallest \ \triangle}{shorter \ leg \ of \ middle \ \triangle} &= \frac{longer \ leg \ of \ smallest \ \triangle}{longer \ leg \ of \ middle \ \triangle}\\ \frac{9}{x} &= \frac{x}{27}\\ x^2 &= 243\\ x &= \sqrt{243} = 9 \sqrt{3}\end{align*}$
::最小腿短腿中腿短腿中腿长腿中腿长腿 9x=x27x2=243x=243=93

Example 5
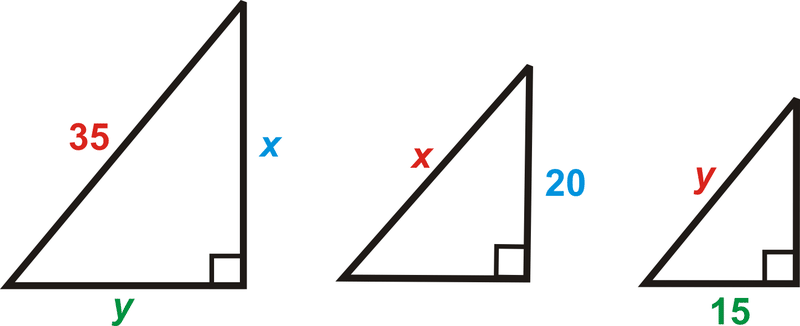
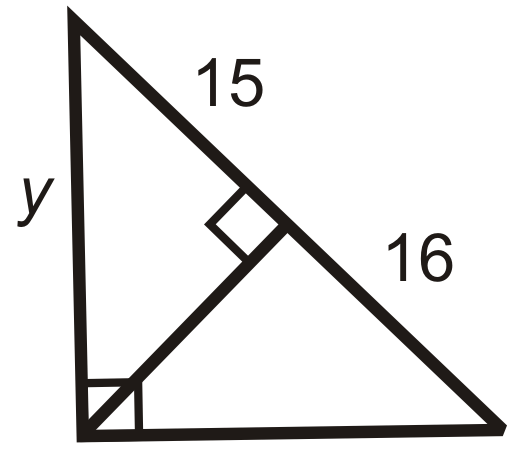
::例5

Find the values of $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ .
::查找 x 和 y 的值。

Separate the triangles. Write a proportion for $\begin{align*}x\end{align*}$ .
::将三角形分开。为 x 写一个比例。

\begin{aligned} \frac{20}{x} & = \frac{x}{35} \\ x^{2} & = 20 \cdot 35 \\ x & = \sqrt{20 \cdot 35} \\ x & = 10 \sqrt{7} \end{aligned}

$\begin{align*}\frac{20}{x} &= \frac{x}{35}\\ x^2 &= 20 \cdot 35\\ x &= \sqrt{20 \cdot 35}\\ x &= 10 \sqrt{7}\end{align*}$
::20x=x35x2=20_35x=20_35x=107

Set up a proportion for $\begin{align*}y\end{align*}$ . Or, now that you know the value of $\begin{align*}x\end{align*}$ you can use the Pythagorean Theorem to solve for $\begin{align*}y\end{align*}$ . Use the method you feel most comfortable with.
::设置y. 的比例, 或者, 如果您知道 x 的值, 您可以使用 Pytagoren 理论解析 y。使用您认为最满意的方法。

\begin{aligned} \frac{15}{y} & = \frac{y}{35} & (10 \sqrt{7})^{2} + y^{2} = 35^{2} \\ y^{2} & = 15 \cdot 35 & 700 + y^{2} = 1225 \\ y & = \sqrt{15 \cdot 35} & y = \sqrt{525} = 5 \sqrt{21} \\ y & = 5 \sqrt{21} \end{aligned}

$\begin{align*}\frac{15}{y} &= \frac{y}{35} && (10 \sqrt{7})^2 + y^2 = 35^2\\ y^2 &= 15 \cdot 35 && \qquad 700 + y^2 =1225\\ y &= \sqrt{15 \cdot 35} && \qquad \qquad \quad \ y = \sqrt{525} = 5 \sqrt{21}\\ y &= 5 \sqrt{21}\end{align*}$
::15y=y35(107)2+y2=352y2=1535700+y2=1225y=1535y=525=521y=521

Review
::回顾

Fill in the blanks.
::填满空白。

$\begin{align*}\triangle BAD \sim \triangle \underline{\;\;\;\;\;\;\;\;\;} \sim \triangle \underline{\;\;\;\;\;\;\;\;\;}\end{align*}$
::

$\begin{align*}\frac{BC}{?} = \frac{?}{CD}\end{align*}$
::BC= CD吗?

$\begin{align*}\frac{BC}{AB} = \frac{AB}{?}\end{align*}$
::BCAB=AB? AB=AB? AB=AB? AB=AB? AB=AB? AB=AB? AB=AB? AB=AB? AB=AB?

$\begin{align*}\frac{?}{AD} = \frac{AD}{BD}\end{align*}$
:AD=亚行)

Write the similarity statement for the right triangles in each diagram.
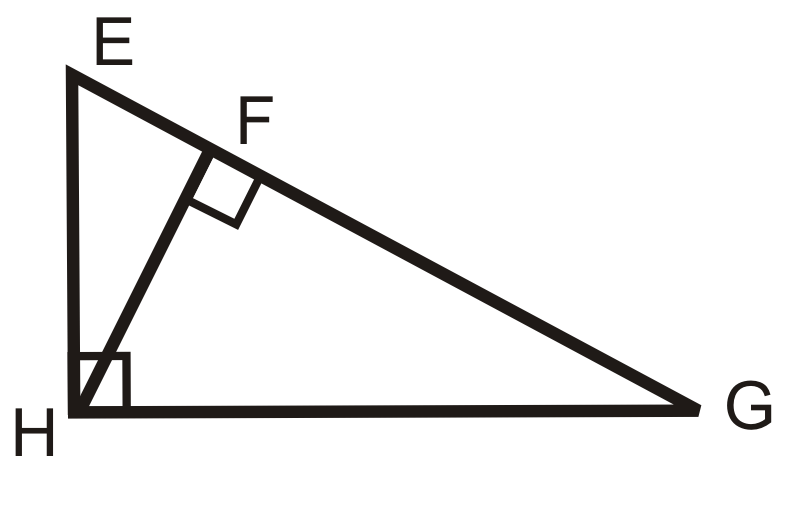
::每个图表中右三角形的相似性说明写出来。

Use the diagram to answer questions 7-10.
::用图表回答问题7 -10

If $\begin{align*}JM = 12\end{align*}$ and $\begin{align*}ML = 9\end{align*}$ , find $\begin{align*}KM\end{align*}$ .
::如果JM=12和ML=9, 找到KM。

Find $\begin{align*}JK\end{align*}$ .
::找到JK。找到JK。

Find $\begin{align*}KL\end{align*}$ .
::寻找 KL 。

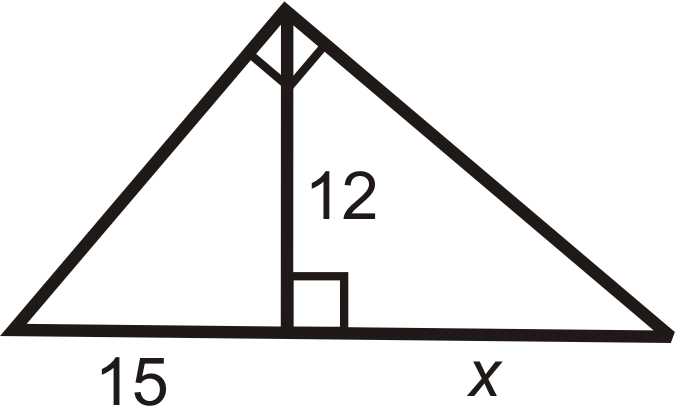
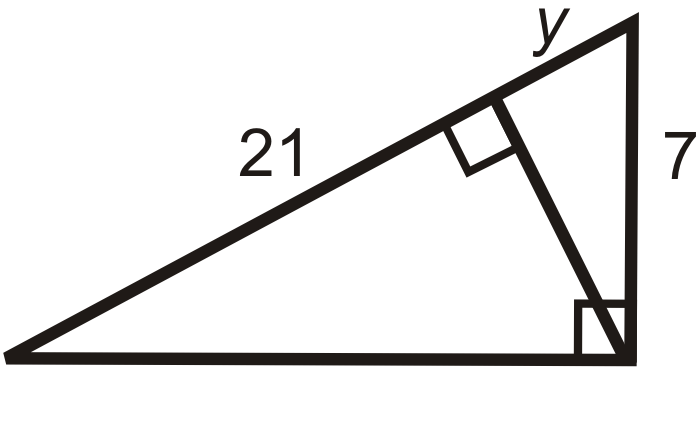
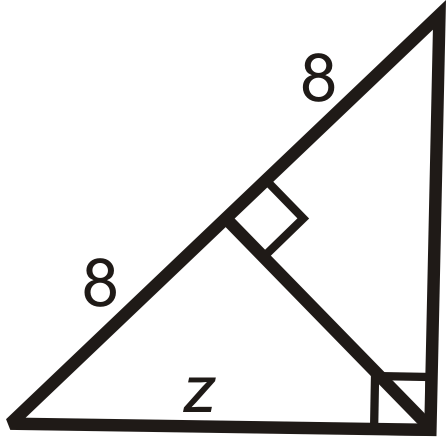
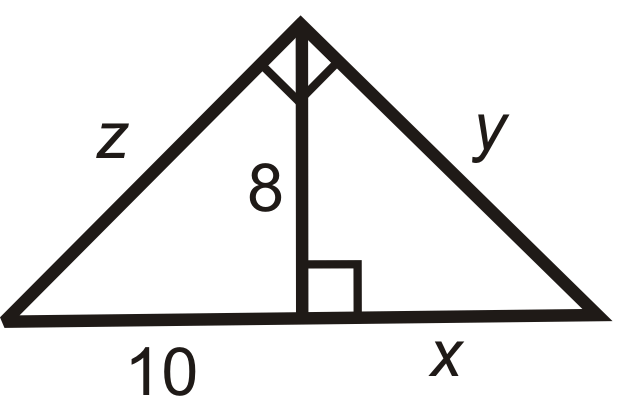
Find the length of the missing variable(s). Simplify all radicals.
::查找缺失变量的长度。简化所有基数。

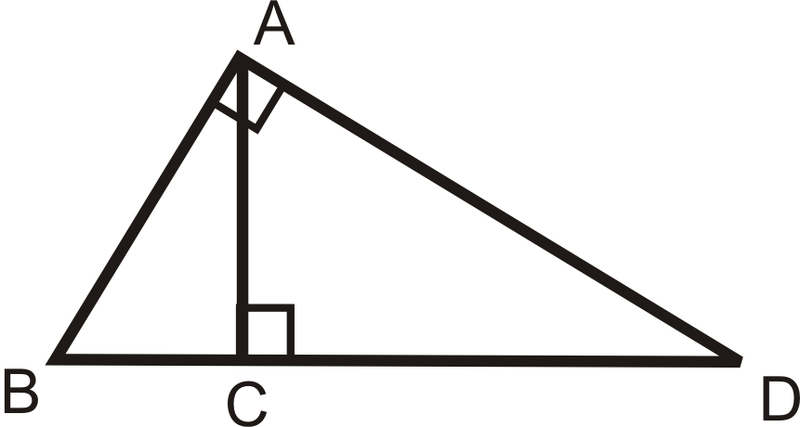
Fill in the blanks of the proof for the Inscribed Similar Triangles Theorem.
::填上类似三角定理的空白证据。

Given : $\begin{align*}\triangle ABD\end{align*}$ with $\begin{align*}\overline{AC} \perp \overline {DB}\end{align*}$ and $\begin{align*}\angle DAB\end{align*}$ is a right angle.
::依据: AC DB ABD 和 AC DB AB 是一个正确角度。

Prove : $\begin{align*}\triangle ABD \sim \triangle CBA \sim \triangle CAD\end{align*}$
::证明:@ABDCBACAAD

*Statement*	*Reason*
1.	1. Given
2. $\begin{align}\angle DCA\end{align}$ and $\begin{align}\angle ACB\end{align}$ are right angles	2.
3. $\begin{align}\angle DAB \cong \angle DCA \cong \angle ACB\end{align}$	3.
4.	4. Reflexive PoC
5.	5. AA Similarity Postulate
6. $\begin{align}B \cong \angle B\end{align}$	6.
7. $\begin{align}\triangle CBA \cong \triangle ABD\end{align}$	7.
8. $\begin{align}\triangle CAD \cong \triangle CBA\end{align}$	8.

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

类似三角形

Inscribed Similar Triangles Theorem ::类似三角类似定理

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Inscribed Similar Triangles Theorem
::类似三角类似定理

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)