8.5 45-45-90 右三角

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 45-45-90 右三角

  Collapse Expand

  45-45-90 右三角

  播放段落

  45-45-90 Right Triangles
  ::45-45-90 右三角

  播放段落

  A right triangle with congruent legs and acute angles is an Isosceles Right Triangle . This triangle is also called a 45-45-90 triangle (named after the angle measures).
  ::右三角形,与腿和尖角相容,是Isosceles右三角形。这个三角形也称为45-45-90三角形(以角度量命名)。

  播放段落

  $\begin{align*}\triangle ABC\end{align*}$ is a right triangle with $\begin{align*}m \angle A = 90^\circ\end{align*}$ , $\begin{align*} \overline {AB} \cong \overline{AC}\end{align*}$ and $\begin{align*}m \angle B = m \angle C = 45^\circ\end{align*}$ .
  ::ABC是右三角形,与mA=90,AB=AC和mB=45。

  播放段落

  45-45-90 Theorem : If a right triangle is isosceles, then its sides are in the ratio $\begin{align*}x:x:x \sqrt{2}\end{align*}$ . For any isosceles right triangle, the legs are $\begin{align*}x\end{align*}$ and the hypotenuse is always $\begin{align*}x \sqrt{2}\end{align*}$ .
  ::45-45-90 理论论: 如果右三角为等分形,则其侧面在比率x:x:x2.中。 对于任何右三角的等分形,腿为x,下限始终为x2。

  播放段落

  What if you were given an isosceles right triangle and the length of one of its sides? How could you figure out the lengths of its other sides?
  ::假若你们获得一个右三角形和其两侧的长度的等分形,你们怎么知道那两侧的长度呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Find the length of $\begin{align*}x\end{align*}$ .
  ::查找 x 的长度。

  

  播放段落

  Use the  $\begin{align*}x:x:x \sqrt{2}\end{align*}$  ratio.
  ::使用 x:x:x2 比例 。

  播放段落

  Here, we are given the hypotenuse. Solve for $\begin{align*}x\end{align*}$ in the ratio.
  ::在这里,我们得到了下限,在比例中解决 x 。

  播放段落

  $$\begin{align*}x \sqrt{2} &= 16\\ x &= \frac{16}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{16 \sqrt{2}}{2} = 8 \sqrt{2}\end{align*}$$
  ::x2=16x=162_22=1622=82

  播放段落

  Example 2
  ::例2

  播放段落

  Find the length of  $\begin{align*}x\end{align*}$ , where  $\begin{align*}x\end{align*}$ is the hypotenuse of a 45-45-90 triangle with leg lengths of $\begin{align*}5\sqrt{3}\end{align*}$ .
  ::查找 x 的长度, x 是45- 45- 90三角形的下拉值, 腿长为53。

  播放段落

  Use the $\begin{align*}x:x:x \sqrt{2}\end{align*}$ ratio.
  ::使用 x:x:x2 比例 。

  播放段落

  $\begin{align*}x=5\sqrt{3}\cdot \sqrt{2}=5\sqrt{6}\end{align*}$
  ::x=532=56

  播放段落

  Example 3
  ::例3

  播放段落

  Find the length of the missing side.
  ::查找缺失方的长度 。

  

  播放段落

  Use the $\begin{align*}x:x:x \sqrt{2}\end{align*}$ ratio. $\begin{align*}TV = 6\end{align*}$ because it is equal to $\begin{align*}ST\end{align*}$ . So, $\begin{align*}SV = 6 \cdot \sqrt{2} = 6 \sqrt{2}\end{align*}$ .
  ::使用 x: x: x2 比率。 TV=6 因为它等于 ST. 所以, SV= 62= 62 。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the length of the missing side.
  ::查找缺失方的长度 。

  

  播放段落

  Use the $\begin{align*}x:x:x \sqrt{2}\end{align*}$ ratio. $\begin{align*}AB = 9 \sqrt{2}\end{align*}$ because it is equal to $\begin{align*}AC\end{align*}$ . So, $\begin{align*}BC = 9 \sqrt{2} \cdot \sqrt{2} = 9 \cdot 2 = 18\end{align*}$ .
  ::使用 x:x:x2 比率。 AB=92 因为它等于 AC。 所以, BC= 92_ 2= 9_2= 18。

  播放段落

  Example 5
  ::例5

  播放段落

  A square has a diagonal with length 10, what are the lengths of the sides?
  ::方形有对角线,长度10,两边的长度是多少?

  播放段落

  Draw a picture.
  ::画一张画。

  

  播放段落

  We know half of a square is a 45-45-90 triangle, so $\begin{align*}10=s \sqrt{2}\end{align*}$ .
  ::我们知道半平方是45 -45 -90三角形 所以10=S2

  播放段落

  $$\begin{align*}s \sqrt{2} &= 10\\ s &= \frac{10}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}= \frac{10 \sqrt{2}}{2}=5 \sqrt{2}\end{align*}$$
  ::s2=10s=1022=1022=52

  播放段落

  Review
  ::回顾

  播放段落
  1. In an isosceles right triangle, if a leg is 4, then the hypotenuse is __________.
     ::在右三角形的等离子体中,如果一条腿是4,那么下限是。
  播放段落
  2. In an isosceles right triangle, if a leg is $\begin{align*}x\end{align*}$ , then the hypotenuse is __________.
     ::在右三角形的等离子体中,如果一条腿是x,则下限为。
  播放段落
  3. A square has sides of length 15. What is the length of the diagonal?
     ::方形有15长的两边,对角的长度是多少?
  播放段落
  4. A square’s diagonal is 22. What is the length of each side?
     ::方形对角是22, 每边的长度是多少?

  播放段落

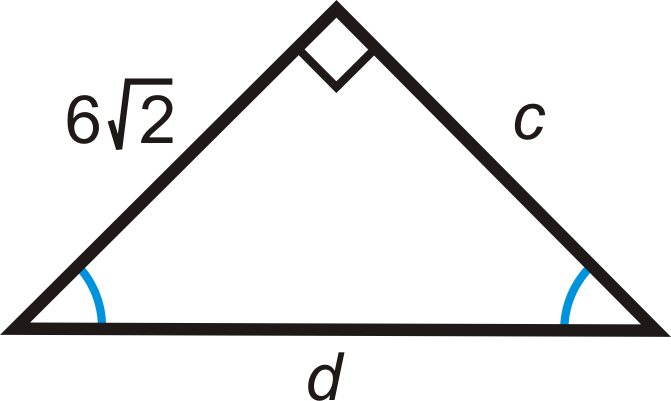
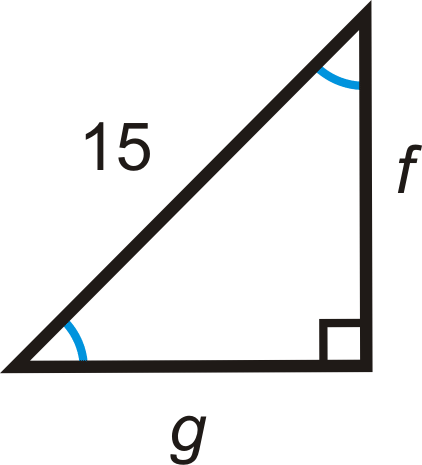
  For questions 5-11, find the lengths of the missing sides. Simplify all radicals.
  ::问题5-11,找出失踪方的长度,简化所有激进分子。

  5. 
  6. 
  7. 
  8. 
  9. 
  10. 
  11. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源