8.6 30-60-90 右三角

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 30-60-90 右三角

  Collapse Expand

  30-60-90 右三角

  播放段落

  30-60-90 Right Triangles
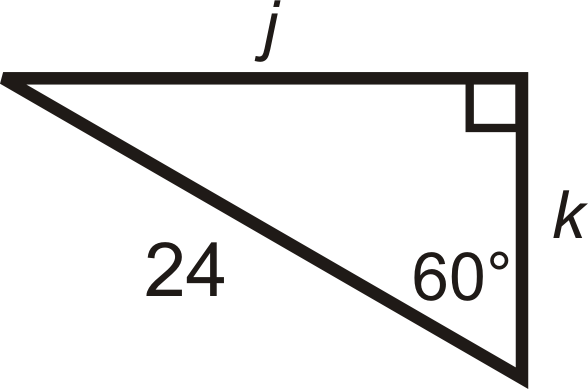
  ::30-60-90 右三角

  播放段落

  One of the two special right triangles is called a 30-60-90 triangle , after its three angles .
  ::两个特别右三角中有一个 叫做30-60-90三角, 沿着三个角度。

  播放段落

  30-60-90 Theorem : If a triangle has angle measures $\begin{array}{r}{30}^{\circ },{60}^{\circ }\end{array}$ and $\begin{array}{r}{90}^{\circ }\end{array}$ , then the sides are in the ratio $\begin{array}{r}x:x\sqrt{3}:2x\end{array}$ .
  ::30 - 60 - 90 理论: 如果三角形角测量 30, 60 和 90, 那么两边的比值是 x: x3: 2x 。

  播放段落

  The shorter leg is always $\begin{array}{r}x\end{array}$ , the longer leg is always $\begin{array}{r}x\sqrt{3}\end{array}$ , and the hypotenuse is always $\begin{array}{r}2x\end{array}$ . If you ever forget these theorems, you can still use the Pythagorean Theorem .
  ::短腿总是 x, 长腿总是 x3, 低脚总是 2x。 如果您忘记这些定理, 您仍然可以使用 Pythagorean 定理 。

  播放段落

  What if you were given a 30-60-90 right triangle and the length of one of its side? How could you figure out the lengths of its other sides?
  ::如果你们获得一个30-60-90的右三角形,以及其中一方的长度呢?你们怎能知道另一边的长度呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Find the value of $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ .
  ::查找 x 和 y 的值。

  

  播放段落

  We are given the longer leg.
  ::我们得到了长腿。

  播放段落

  $$\begin{array}{rl}& x\sqrt{3}=12\\ & x=\frac{12}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{12\sqrt{3}}{3}=4\sqrt{3}\\ & \text{The hypotenuse is}\\ & y=2(4\sqrt{3})=8\sqrt{3}\end{array}$$

  
  ::x3=12x=12333=1233=43 下限值为2(43)=83

  播放段落

  Example 2
  ::例2

  播放段落

  Find the value of  $\begin{array}{r}x\end{array}$  and  $\begin{array}{r}y\end{array}$ .
  ::查找 x 和 y 的值。

  

  播放段落

  We are given the hypotenuse.
  ::我们被赋予了下限。

  播放段落

  $$\begin{array}{rl}& 2x=16\\ & x=8\\ & \text{The longer leg is}\\ & y=8\cdot \sqrt{3}=8\sqrt{3}\end{array}$$

  
  ::2x=16x=8 长腿=83=83

  播放段落

  Example 3
  ::例3

  播放段落

  Find the length of the missing sides.
  ::查找缺失方的长度 。

  

  播放段落

  We are given the shorter leg. If $\begin{array}{r}x=5\end{array}$ , then the longer leg, $\begin{array}{r}b=5\sqrt{3}\end{array}$ , and the hypotenuse, $\begin{array}{r}c=2(5)=10\end{array}$ .
  ::我们得到了短腿。 如果 x=5, 那么长腿, b=53, 和下限, c=2(5)=10。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the length of the missing sides.
  ::查找缺失方的长度 。

  

  播放段落

  We are given the hypotenuse. $\begin{array}{r}2x=20\end{array}$ , so the shorter leg, $\begin{array}{r}f=\frac{20}{2}=10\end{array}$ , and the longer leg, $\begin{array}{r}g=10\sqrt{3}\end{array}$ .
  ::2x=20,所以短腿F=202=10,长腿g=103。

  播放段落

  Example 5
  ::例5

  播放段落

  A rectangle has sides 4 and $\begin{array}{r}4\sqrt{3}\end{array}$ . What is the length of the diagonal ?
  ::矩形有4和43两边,对角的长度是多少?

  播放段落

  If you are not given a picture, draw one.
  ::如果您没有获得图片,请绘制一张。

  

  播放段落

  The two lengths are $\begin{array}{r}x,x\sqrt{3}\end{array}$ , so the diagonal would be $\begin{array}{r}2x\end{array}$ , or $\begin{array}{r}2(4)=8\end{array}$ .
  ::两长为xx3,对角为2x或2(4)=8。

  播放段落

  If you did not recognize this is a 30-60-90 triangle, you can use the Pythagorean Theorem too.
  ::如果你没认出这是30 -60 -90三角形 你可以使用毕达哥伦神话

  播放段落

  $$\begin{array}{rl}{4}^2+{\left(4\sqrt{3}\right)}^2& =d^2\\ 16+48& =d^2\\ d& =\sqrt{64}=8\end{array}$$

  
  ::42+(43)2=d216+48=d2d=64=8

  播放段落

  Review
  ::回顾

  播放段落
  1. In a 30-60-90 triangle, if the shorter leg is 5, then the longer leg is __________ and the hypotenuse is ___________.
     ::在30-60-90三角形中,如果短腿为5,则长腿为________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
  播放段落
  2. In a 30-60-90 triangle, if the shorter leg is $\begin{array}{r}x\end{array}$ , then the longer leg is __________ and the hypotenuse is ___________.
     ::在30-60-90三角形中,如果短腿为x,则长腿为,下限为。
  播放段落
  3. A rectangle has sides of length 6 and $\begin{array}{r}6\sqrt{3}\end{array}$ . What is the length of the diagonal?
     ::矩形有6和63长的两边,对角线的长度是多少?
  播放段落
  4. Two (opposite) sides of a rectangle are 10 and the diagonal is 20. What is the length of the other two sides?
     ::矩形的两面(对面)是10,对角是20,其他两面的长度是多少?

  播放段落

  For questions 5-12, find the lengths of the missing sides. Simplify all radicals.
  ::问题5 - 12, 找出失踪方的长度, 简化所有激进分子 。

  5. 
  6. 
  7. 
  8. 
  9. 
  10. 
  11. 
  12. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源