Course: 2.15 期间和频率 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 期间和频率

Collapse Expand
期间和频率
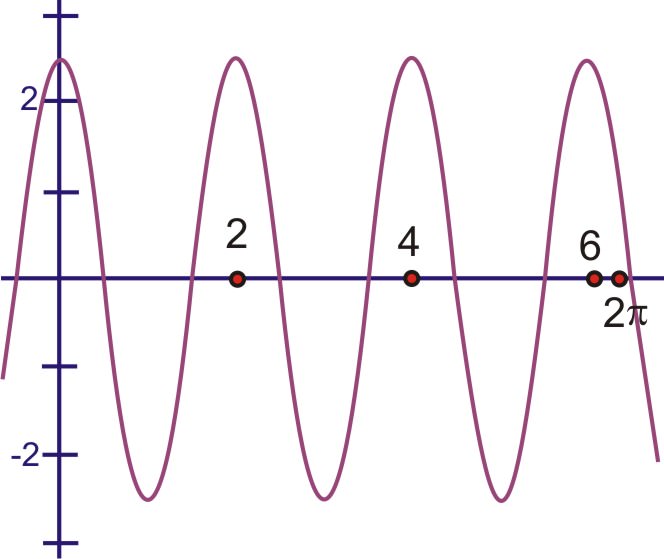
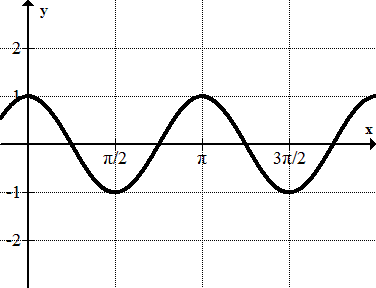
While working on an assignment about sound in your science class, your Instructor informs you that what you know as the "pitch" of a sound is, in fact, the frequency of the sound waves. He then plays a note on a musical instrument, and the pattern of the sound wave on a graph looks like this:
::在你的科学课里,教官在研究关于声音的任务时告诉你,你所知道的声音的“弹道”其实是声波的频率。他然后在乐器上演奏一个音符, 而声波在图表上的规律是这样的:

He then tells you to find the frequency of the sound wave from the graph? Can you do it?
::然后他告诉你从图中找到声波的频率,你能做到吗?

Period and Frequency
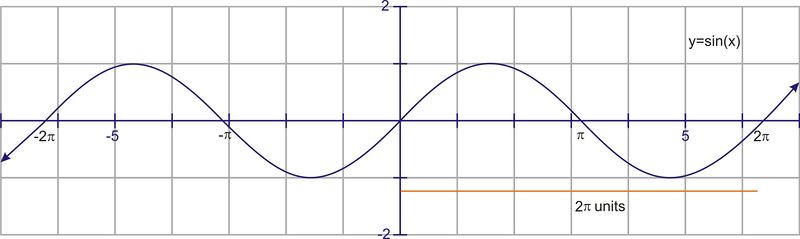
::期间和频率

The period of a trigonometric function is the horizontal distance traversed before the $\begin{aligned} y - \end{aligned}$ values begin to repeat. For both graphs, $\begin{aligned} y = \sin x \end{aligned}$ and $\begin{aligned} y = \cos x \end{aligned}$ , the period is $\begin{aligned} 2 π . \end{aligned}$ As you may remember, after completing one rotation of the unit circle , these values are the same.
::三角函数的期间是y- 值开始重复之前的水平距离。对于两个图形, y=sinx 和y=cosx, 时间段为 2。正如您可能记得的那样, 在完成单位圆的旋转后, 这些数值是相同的。

Frequency is a measurement that is closely related to period. In science, the frequency of a sound or light wave is the number of complete waves for a given time period (like seconds). In trigonometry, because all of these periodic functions are based on the unit circle, we usually measure frequency as the number of complete waves every $\begin{aligned} 2 π \end{aligned}$ units. Because $\begin{aligned} y = \sin x \end{aligned}$ and $\begin{aligned} y = \cos x \end{aligned}$ cover exactly one complete wave over this interval, their frequency is 1.
::频率是一种与周期密切相关的测量方法。在科学中,声音或光波的频率是特定时间段的完整波(类似秒)的数量。在三角测量中,由于所有这些周期性函数都以单位圆为基础,我们通常将频率作为每2°C单位的完整波数来测量。因为y=sinx和y=cosx在此间隔期间完全覆盖一个完整波数,它们的频率是1。

Period and frequency are inversely related. That is, the higher the frequency (more waves over $\begin{aligned} 2 π \end{aligned}$ units), the lower the period (shorter distance on the $\begin{aligned} x - \end{aligned}$ axis for each complete cycle).
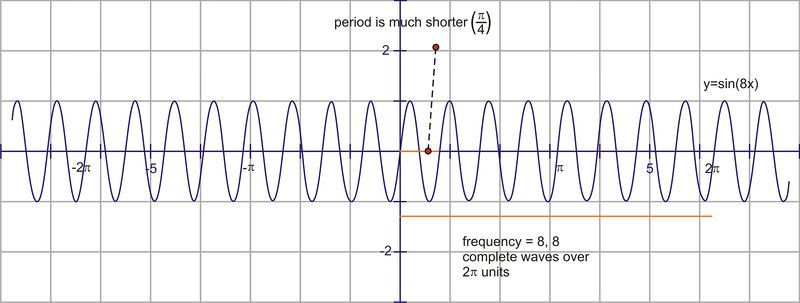
::周期和频率是反比的。也就是说,频率越高( 超过 2 × 单位的波浪越大),周期越低( 每个完整周期的x- 轴距离越短)。

After observing the transformations that result from multiplying a number in front of the sinusoid, it seems natural to look at what happens if we multiply a constant inside the argument of the function, or in other words, by the $\begin{aligned} x \end{aligned}$ value. In general, the equation would be $\begin{aligned} y = \sin B x \end{aligned}$ or $\begin{aligned} y = \cos B x \end{aligned}$ . For example, look at the graphs of $\begin{aligned} y = \cos 2 x \end{aligned}$ and $\begin{aligned} y = \cos x \end{aligned}$ .
::观察在正弦素前面乘数后产生的变异后, 似乎自然地看到如果我们在函数参数的参数内乘以一个常数, 或换句话说, 按 x 值乘以一个常数, 会发生什么。一般来说, 等式是 y=sinBx 或 y=cosBx 。例如, 查看 y=cos2x 和 y=cosx 的图形。

Notice that the number of waves for $\begin{aligned} y = \cos 2 x \end{aligned}$ has increased, in the same interval as $\begin{aligned} y = \cos x \end{aligned}$ . There are now 2 waves over the interval from 0 to $\begin{aligned} 2 π \end{aligned}$ . Consider that you are doubling each of the $\begin{aligned} x \end{aligned}$ values because the function is $\begin{aligned} 2 x \end{aligned}$ . When $\begin{aligned} π \end{aligned}$ is plugged in, for example, the function becomes $\begin{aligned} 2 π \end{aligned}$ . So the portion of the graph that normally corresponds to $\begin{aligned} 2 π \end{aligned}$ units on the $\begin{aligned} x - \end{aligned}$ axis, now corresponds to half that distance—so the graph has been “scrunched” horizontally. The frequency of this graph is therefore 2, or the same as the constant we multiplied by in the argument. The period (the length for each complete wave) is $\begin{aligned} π \end{aligned}$ .
::请注意 y= cos= @% 2x 的波数已经增加, 与 y= cos=%x 的间隔相同。现在间隔间距为 0 到 2 。认为您正在将每个 x 值翻一倍, 因为函数是 2x 。例如, 当插入时, 函数就变成 2 。因此, 图中通常与 x - 轴上 2 + 单位相对应的部分, 现在与此距离的一半相对应 - 因此, 图表是水平“ 缩小” 的。因此, 此图的频率是 2 , 或者与参数中我们乘以的常数相同。时间段( 每个完整波的长度) 是。

Finding the Period and Frequency
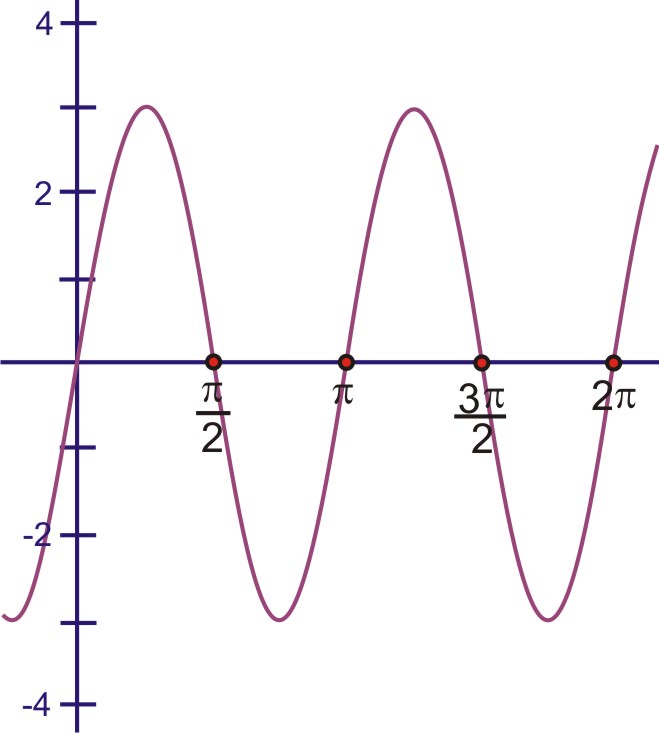
::时间和频率

1. What is the frequency and period of $\begin{aligned} y = \sin 3 x \end{aligned}$ ?
::1. y=sin*3x的频率和期间是多少?

If we follow the pattern from the previous example, multiplying the angle by 3 should result in the sine wave completing a cycle three times as often as $\begin{aligned} y = \sin x \end{aligned}$ . So, there will be three complete waves if we graph it from 0 to $\begin{aligned} 2 π \end{aligned}$ . The frequency is therefore 3. Similarly, if there are 3 complete waves in $\begin{aligned} 2 π \end{aligned}$ units, one wave will be a third of that distance, or $\begin{aligned} \frac{2 π}{3} \end{aligned}$ radians. Here is the graph:
::如果我们遵循上一个示例的图案, 将角度乘以 3 将使正弦波完成一个周期, 频率是y=sinx的三倍。因此, 如果我们将它从 0 到 2 。因此, 频率是 3 。同样, 如果在 2 单位中有 3 个完整波, 一个波将是该距离的三分之一, 或者 23 弧度。下面是图表 :

This number that is multiplied by $\begin{aligned} x \end{aligned}$ , called $\begin{aligned} B \end{aligned}$ , will create a horizontal dilation. The larger the value of $\begin{aligned} B \end{aligned}$ , the more compressed the waves will be horizontally. To stretch out the graph horizontally, we would need to decrease the frequency, or multiply by a number that is less than 1. Remember that this dilation factor is inversely related to the period of the graph.
::乘以 x 的这个数字, 称为 B, 将产生水平扩张。 B 值越大, 波的压缩度越大。要水平延伸图形, 我们需要降低频率, 或乘以小于 1 的数。请记住, 这个放大系数与图形的周期反相联。

Adding, one last time to our equations from before, we now have: $\begin{aligned} y = D \pm A \sin (B (x \pm C)) \end{aligned}$ or $\begin{aligned} y = D \pm A \cos (B (x \pm C)) \end{aligned}$ , where $\begin{aligned} B \end{aligned}$ is the frequency, the period is equal to $\begin{aligned} \frac{2 π}{B} \end{aligned}$ , and everything else is as defined before.
::添加, 上次我们之前的方程, 现在有: y= D {Asin} (B(x}C) ) 或 y= D {Acos} (B(x}C) ) , B 是频率, 周期等于 2 B , 其它一切都如前所述。

2. What is the frequency and period of $\begin{aligned} y = \cos \frac{1}{4} x \end{aligned}$ ?
::2. y=cos=14x的频率和时间段是多少?

Using the generalization above, the frequency must be $\begin{aligned} \frac{1}{4} \end{aligned}$ and therefore the period is $\begin{aligned} \frac{\frac{2 π}{1}}{\frac{1}{4}} \end{aligned}$ , which simplifies to: $\begin{aligned} \frac{2 π}{\frac{1}{4}} = \frac{\frac{2 π}{1}}{\frac{1}{4}} \cdot \frac{\frac{4}{1}}{\frac{4}{1}} = \frac{8 π}{1} = 8 π \end{aligned}$
::使用上文的概括,频率必须是14,因此周期是2 114,简化为:2 14=2 11441=81=8

Thinking of it as a transformation, the graph is stretched horizontally. We would only see $\begin{aligned} \frac{1}{4} \end{aligned}$ of the curve if we graphed the function from 0 to $\begin{aligned} 2 π \end{aligned}$ . To see a complete wave, therefore, we would have to go four times as far, or all the way from 0 to $\begin{aligned} 8 π \end{aligned}$ .
::将图视为一个转换, 图表是水平拉伸的。如果我们将函数从 0 绘制成图到 2 , 我们只能看到 14 个曲线。因此, 要看到一个完整的波, 我们只能走4 次, 或者从 0 到 8 。

3. What is the frequency and period of $\begin{aligned} y = \sin \frac{1}{2} x \end{aligned}$ ?
::3. y=sin12x的频率和时间段是多少?

Like the previous two problems, we can see that the frequency is $\begin{aligned} \frac{1}{2} \end{aligned}$ , and so the period is $\begin{aligned} \frac{\frac{2 π}{1}}{\frac{1}{2}} \end{aligned}$ , which becomes $\begin{aligned} 2 π \times \frac{2}{1} = 4 π \end{aligned}$
::与前两个问题一样,我们可以看到频率是12, 所以这个周期是2 112, 变成2 21=4 。

Examples
::实例

Example 1
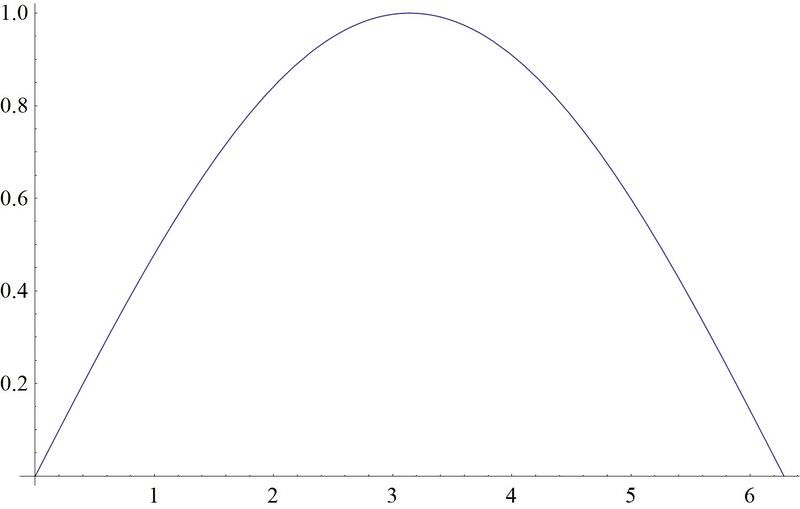
::例1

Earlier, you were asked to find the frequency of the sound wave from the graph.
::早些时候,有人要求你从图表中找到声波的频率。

By inspecting the graph
::通过检查图表

You can see that the wave takes about 6.2 seconds to make one complete cycle. This means that the frequency of the wave is approximately 1 cycle per second (since $\begin{aligned} 2 π \end{aligned}$ is approximately 6.28). (You should note that in a real wave of sound, you would need to use the speed of the wave and so the calculation would be different. But if you read the graph the same way you read trigonometric functions to find the frequency, this is the result you would find.)
::可以看到波需要大约6.2秒来完成一个完整的周期。这意味着波的频率大约是每秒1个周期( 因为 2大约是6.28) 。 (您应该注意, 在真正的音波波中, 您需要使用波的速度, 这样计算就会不同。但是, 如果您以相同的方式读取三角函数来找到频率, 这是您会找到的结果 ) 。

Example 2
::例2

Draw a sketch of $\begin{aligned} y = 3 \sin 2 x \end{aligned}$ from 0 to $\begin{aligned} 2 π \end{aligned}$ .
::绘制 y= 3sin%% 2x 从 0 到 2 的草图。

The "2" inside the sine function makes the function "squashed" by a factor of 2 in the horizontal direction.
::正弦函数中的“ 2” 使函数在水平方向上“ 平整” 以 2 的乘数“ 压断 ” 。

Example 3
::例3

Draw a sketch of $\begin{aligned} y = 2.5 \cos π x \end{aligned}$ from 0 to $\begin{aligned} 2 π \end{aligned}$ .
::绘制 y= 2.5cosx 从 0 到 2 的草图。

The $\begin{aligned} π \end{aligned}$ inside the sine function makes the function "squashed" by a factor of $\begin{aligned} π \end{aligned}$ in the horizontal direction.
::在正弦函数中,正弦函数使函数在水平方向上“折叠”成“折叠”因子。

Example 4
::例4

Draw a sketch of $\begin{aligned} y = 4 \sin \frac{1}{2} x \end{aligned}$ from 0 to $\begin{aligned} 2 π \end{aligned}$ .
::绘制 y= 4sin 12x 从 0 到 2 的草图。

The $\begin{aligned} \frac{1}{2} \end{aligned}$ inside the sine function makes the function "stretched" by a factor of $\begin{aligned} \frac{1}{2} \end{aligned}$ in the horizontal direction.
::正弦函数中的 12 使该函数在水平方向上“拉伸” 12 倍。

Review
::回顾

Find the period and frequency of each function below.
::确定以下每项职能的期限和频率。

$\begin{aligned} y = \sin (4 x) \end{aligned}$
::y=sin( 4x)

$\begin{aligned} y = \cos (2 x) \end{aligned}$
::y=cos( 2x)

$\begin{aligned} y = \cos (\frac{1}{2} x) \end{aligned}$
::y=cos( 12x)

$\begin{aligned} y = \sin (\frac{3}{4} x) \end{aligned}$
::y=sin( 34x)

$\begin{aligned} y = \sin (3 x) \end{aligned}$
::y=sin( 3x)

Draw a sketch of each function from 0 to $\begin{aligned} 2 π \end{aligned}$ .
::绘制从 0 到 2 的每个函数的草图。

$\begin{aligned} y = \sin (3 x) \end{aligned}$
::y=sin( 3x)

$\begin{aligned} y = \cos (5 x) \end{aligned}$
::y=cos( 5x)

$\begin{aligned} y = 3 \cos (\frac{2}{5} x) \end{aligned}$
::y=3cos( 25x)

$\begin{aligned} y = \frac{1}{2} \sin (\frac{3}{4} x) \end{aligned}$
::y=12sin( 34x)

$\begin{aligned} y = - \sin (2 x) \end{aligned}$
::ysin( 2x)

$\begin{aligned} y = \tan (3 x) \end{aligned}$
::y=tan( 3x)

$\begin{aligned} y = \sec (2 x) \end{aligned}$
::y=sec( 2x)

$\begin{aligned} y = \csc (4 x) \end{aligned}$
::y=csc( 4x)

Find the equation of each function. Assume there is no horizontal translation.
::查找每个函数的方程式。假设没有水平翻译。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

期间和频率

Period and Frequency ::期间和频率

Finding the Period and Frequency ::时间和频率

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Period and Frequency
::期间和频率

Finding the Period and Frequency
::时间和频率

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)