课程： 8.7 松、脊弦、唐

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节顺弦、顺弦、正弦

折叠展开
顺弦、顺弦、正弦
Sine, Cosine, and Tangent
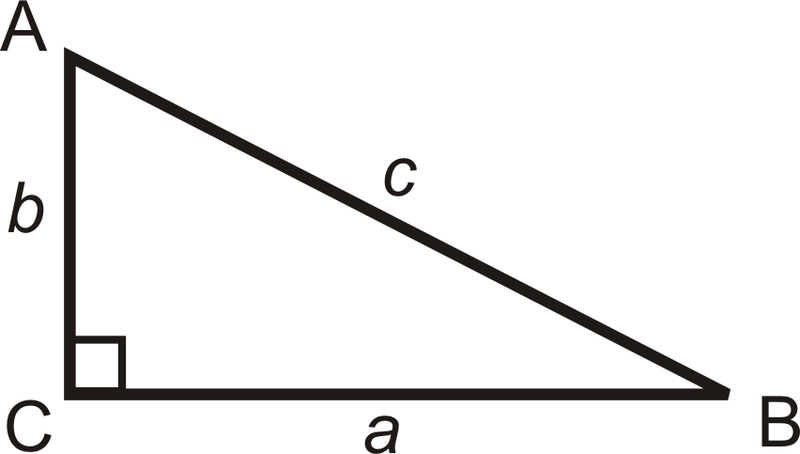
::顺弦、顺弦和唐敏

Trigonometry is the study of the relationships between the sides and angles of right triangles. The legs are called adjacent or opposite depending on which acute angle is being used.
::三角形是右三角形两侧和角之间的关系研究。双腿被称为相邻或对立, 取决于使用的直角。

$\begin{align*}& a \ \text{is} \ adjacent \ \text{to} \ \angle B \qquad \ a \ \text{is} \ opposite \ \angle A\\ & b \ \text{is} \ adjacent \ \text{to} \ \angle A \qquad \ b \ \text{is} \ opposite \ \angle B\\ & c \ \text{is the} \ hypotenuse\end{align*}$
::a 与 B a 相邻 B a 相对 Ab 与 A b 相邻 Bc 是下限

The three basic trigonometric ratios are called sine, cosine and tangent. For right triangle $\begin{align*}\triangle ABC\end{align*}$ , we have:
::三个基本三角比被称为正弦、正弦和正弦。对于右三角 ABC,我们有:

Sine Ratio: $\begin{align*}\frac{opposite \ leg }{hypotenuse} \ \sin A = \frac{a}{c}\end{align*}$ or $\begin{align*}\sin B = \frac{b}{c}\end{align*}$
::Sine 比率:对面腿血压

Cosine Ratio: $\begin{align*}\frac{adjacent \ leg}{hypotenuse} \ \cos A = \frac{b}{c}\end{align*}$ or $\begin{align*}\cos B = \frac{a}{c}\end{align*}$
::CosA=bc或cosB=ac

Tangent Ratio: $\begin{align*}\frac{opposite \ leg}{adjacent \ leg} \ \tan A = \frac{a}{b}\end{align*}$ or $\begin{align*}\tan B = \frac{b}{a}\end{align*}$
::倾角比率:对面腿相邻腿TanaA=ab或tanB=ba

An easy way to remember ratios is to use SOH-CAH-TOA.
::使用SOH-CAH-TOA是记住比率的一个简单方法。

A few important points:
::几个要点:

Always reduce ratios (fractions) when you can.
::当您能够降低比率时,总是降低比率(违规)。

Use the to find the missing side (if there is one).
::使用此方法查找缺失的一面( 如果有的话 ) 。

If there is a radical in the denominator, rationalize the denominator.
::如果分母中有一个激进的分母,那么理顺分母。

What if you were given a right triangle and told that its sides measure 3, 4, and 5 inches? How could you find the sine, cosine, and tangent of one of the triangle's non-right angles?
::假若你们获得一个对立的三角形,并被告知其两侧的长度是3、4英寸和5英寸,你们怎能发现三角形上一个非对立角度的正弦、正弦和正弦呢?

Examples
::实例

Example 1
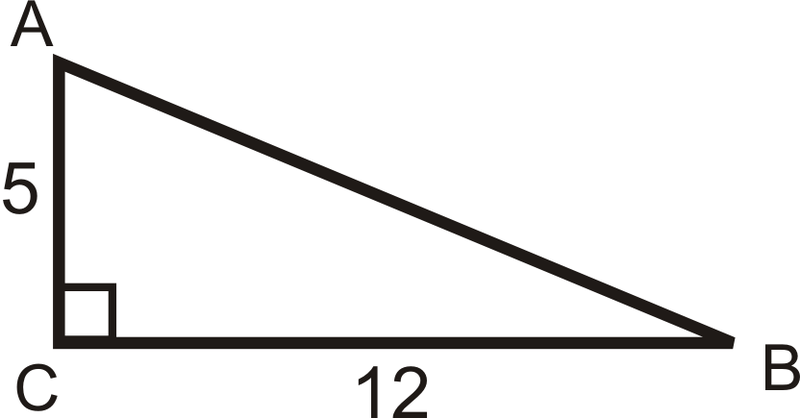
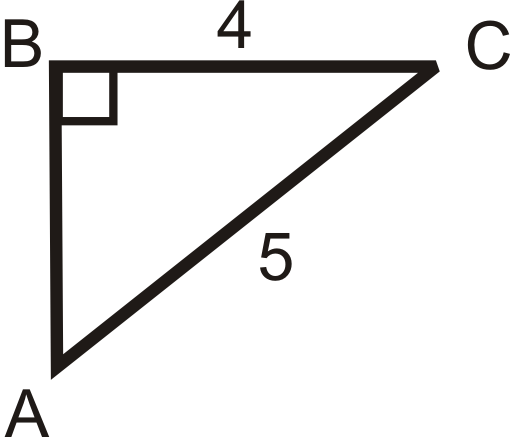
::例1

Find the sine, cosine and tangent ratios of $\begin{align*}\angle A\end{align*}$ .
::找到QA的正弦、连弦和正弦比例。

First, we need to use the Pythagorean Theorem to find the length of the hypotenuse.
::首先,我们需要利用毕达哥里安神话来找到低温的长度

$\begin{align*}5^2 + 12^2 &= c^2\\ 13 &= c\\ \sin A &= \frac{leg \ opposite \ \angle A}{hypotenuse} = \frac{12}{13} && \cos A = \frac{leg \ adjacent \ to \ \angle A}{hypotenuse}= \frac{5}{13},\\ \tan A &= \frac{leg \ opposite \ \angle A}{leg \ adjacent \ to \ \angle A}= \frac{12}{5}\end{align*}$
::52+122=c213=csinA=对面的Aleg @ahypotenuse=1213cosA=靠近@Ahypotenuse=513,tanA=对面的Aleg=@A=125

Example 2
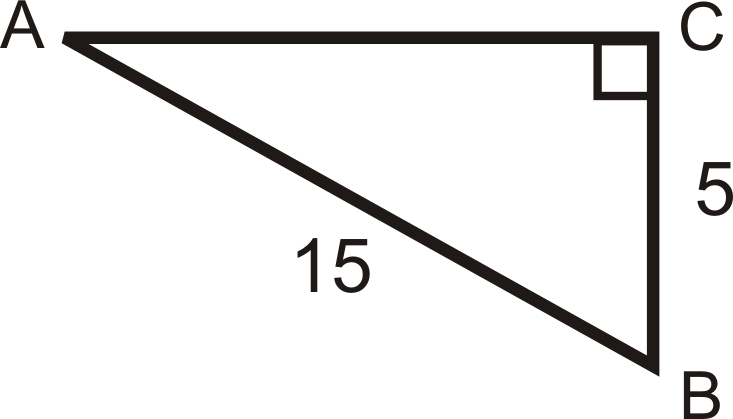
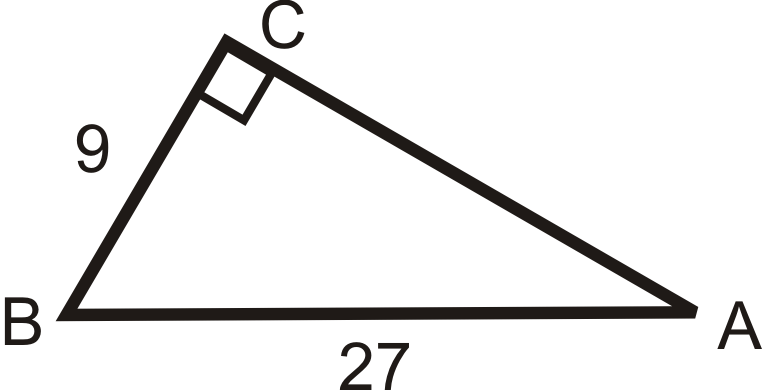
::例2

Find the sine, cosine, and tangent of $\begin{align*}\angle B\end{align*}$ .
::找到ZB的正弦、连弦和正弦

Find the length of the missing side.
::查找缺失方的长度。

$\begin{align*}AC^2 + 5^2 &= 15^2\\ AC^2 &= 200\\ AC &= 10 \sqrt{2}\\ \sin B &= \frac{10 \sqrt{2}}{15} = \frac{2 \sqrt{2}}{3} && \cos B = \frac{5}{15}=\frac{1}{3} && \tan B = \frac{10 \sqrt{2}}{5} = 2 \sqrt{2}\end{align*}$
::AC2+52=152AC2=200AC=102sinB=10215=223cosB=515=13tanB=1025=22

Example 3
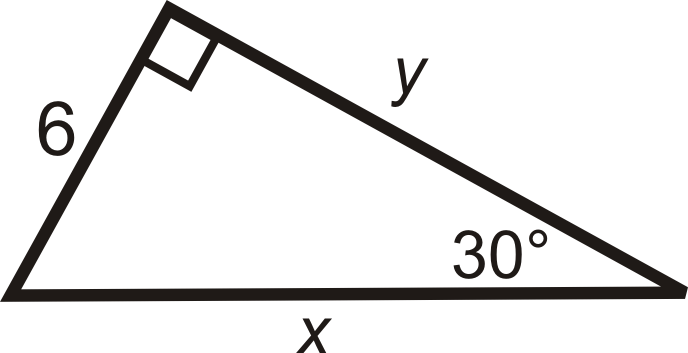
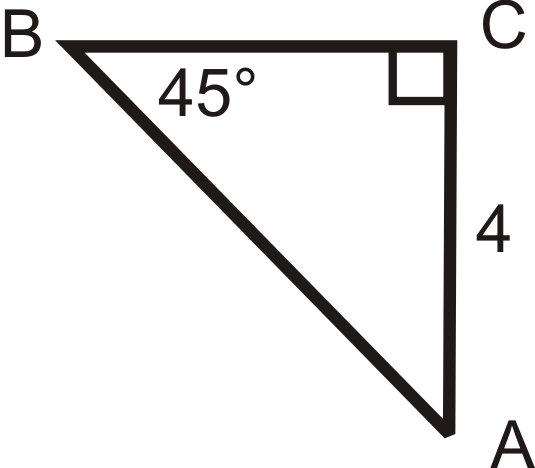
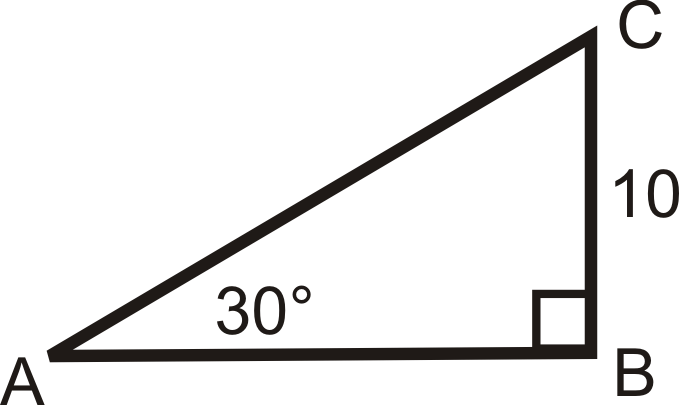
::例3

Find the sine, cosine and tangent of $\begin{align*}30^\circ\end{align*}$ .
::找到正弦,连弦和正弦 30。

This is a 30-60-90 triangle. The short leg is 6, $\begin{align*}y = 6 \sqrt{3}\end{align*}$ and $\begin{align*}x=12\end{align*}$ .
::这是一个 30 - 60 - 90 三角形。短腿是 6 y= 6 - 3 和 x= 12 。

$\begin{align*}\sin 30^\circ = \frac{6}{12} = \frac{1}{2} && \cos 30^\circ = \frac{6 \sqrt{3}}{12} = \frac{\sqrt{3}}{2} && \tan 30^\circ = \frac{6}{6 \sqrt{3}} = \frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}\end{align*}$
::612=12cos30 631232tan30663=13333333

Example 4
::例4

Answer the questions about the following image. Reduce all fractions.
::回答关于以下图像的问题。减少所有分数。

What is $\begin{align*}\sin A\end{align*}$ , $\begin{align*}\cos A\end{align*}$ , and $\begin{align*}\tan A\end{align*}$ ?
::什么是罪A,CASA和TANA?

$\begin{align*}\sin A=\frac{16}{20}=\frac{4}{5}\end{align*}$
::A=1620=45

$\begin{align*} \cos A=\frac{12}{20}=\frac{3}{5}\end{align*}$
::COA=1220=35

$\begin{align*} \tan A=\frac{16}{12}=\frac{4}{3}\end{align*}$
::tanA=1612=43

Review
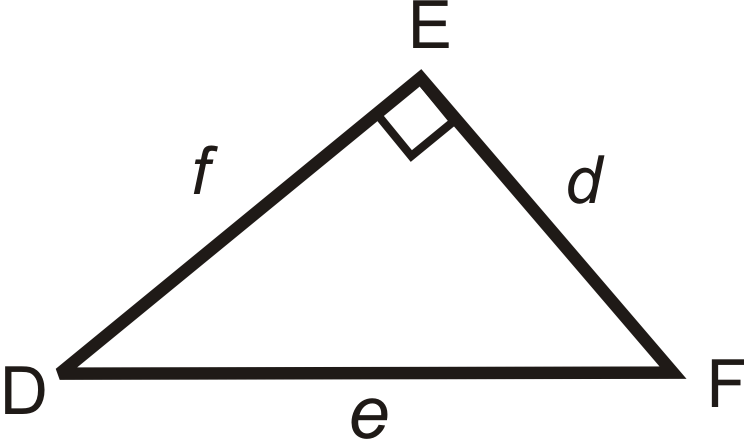
::回顾

Use the diagram to fill in the blanks below.
::使用图表填充下面的空白。

$\begin{align*}\tan D = \frac{?}{?}\end{align*}$
::丹达?

$\begin{align*}\sin F = \frac{?}{?}\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么?

$\begin{align*}\tan F = \frac{?}{?}\end{align*}$
::晒屁股?

$\begin{align*}\cos F = \frac{?}{?}\end{align*}$
::科斯菲? ?

$\begin{align*}\sin D = \frac{?}{?}\end{align*}$
::罪过?

$\begin{align*}\cos D = \frac{?}{?}\end{align*}$
::- COSD? - 是的。 - COSD?

From questions 1-6, we can conclude the following. Fill in the blanks.
::从问题1至6中,我们可以得出以下结论。填写空白。

$\begin{align*}\cos \underline{\;\;\;\;\;\;\;} = \sin F\end{align*}$ and $\begin{align*}\sin \underline{\;\;\;\;\;\;\;} = \cos F\end{align*}$ .
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}CosinF 和sincosF {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我...

$\begin{align*}\tan D\end{align*}$ and $\begin{align*}\tan F\end{align*}$ are _________ of each other.
::相形相形,相形见绌

Find the sine, cosine and tangent of $\begin{align*}\angle A\end{align*}$ . Reduce all fractions and radicals.
::找到QA的正弦、正弦和正弦。减少所有分数和基数。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

常规

顺弦、顺弦、正弦

Sine, Cosine, and Tangent ::顺弦、顺弦和唐敏

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Sine, Cosine, and Tangent
::顺弦、顺弦和唐敏

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源