9.1 圆圈部分

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 圆圈部分

  Collapse Expand

  圆圈部分

  播放段落

  Circles
  ::圆环

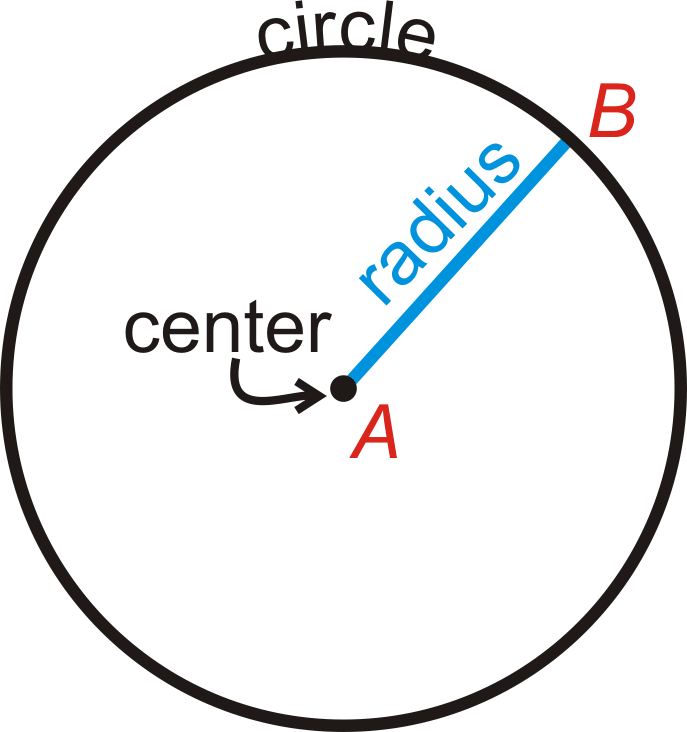
  播放段落

  A circle is the set of all points in the plane that are the same distance away from a specific point , called the center . The center of the circle below is point $\begin{align*}A\end{align*}$ . We call this circle “circle $\begin{align*}A\end{align*}$ ,” and it is labeled $\begin{align*}\bigodot A\end{align*}$ .
  ::一个圆是平面上所有点的集合,这些点与特定点的距离相同,称为中点。下面圆的中心是 A 点。我们称之为“ A 圈 圈 ” , 它被标为 A 。

  

  播放段落

  Important Circle Parts
  ::重要圆环部件

  播放段落

  Radius : The distance from the center of the circle to its outer rim.
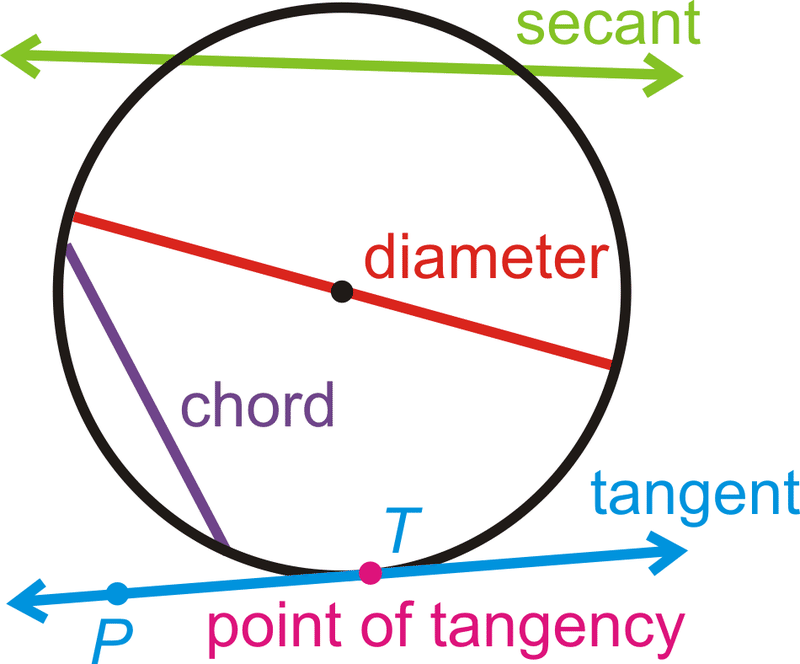
  ::半径:从圆的中心到其外边缘的距离。

  播放段落

  Chord : A line segment whose endpoints are on a circle.
  ::和弦: 一条线段, 其终点在圆上 。

  播放段落

  Diameter : A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius.
  ::直径是半径的两倍。

  播放段落

  Secant : A line that intersects a circle in two points.
  ::secant: 一条将圆交错为两点的线。

  播放段落

  Tangent : A line that intersects a circle in exactly one point.
  ::切线:一线将圆交错在一个点上。

  播放段落

  Point of Tangency : The point where a tangent line touches the circle.
  ::切切点: 相切线接触圆圈的点 。

  

  播放段落

  The tangent ray $\begin{align*}\overrightarrow{TP}\end{align*}$ and tangent segment $\begin{align*}\overline{TP}\end{align*}$ are also called tangents.
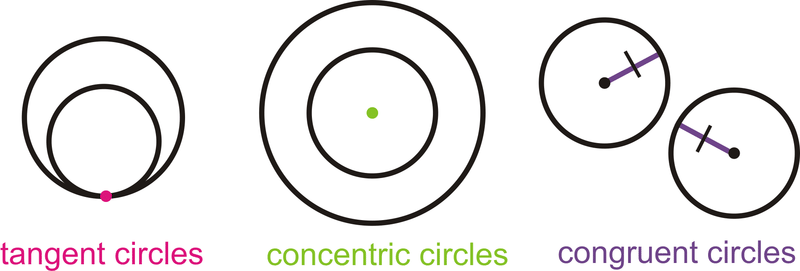
  ::相切的射线“TP”和相切部分“TP”也被称为相切。

  播放段落

  Tangent Circles : Two or more circles that intersect at one point.
  ::切形圆形:两个或两个以上的圆形在一个点上交叉。

  播放段落

  Concentric Circles : Two or more circles that have the same center, but different radii.
  ::共心圆圈:两个或两个以上的圆圈具有相同的中心,但不同的弧度。

  播放段落

  Congruent Circles : Two or more circles with the same radius, but different centers.
  ::共圆:两个或两个以上的圆,半径相同,但中心不同。

  

  播放段落

  What if you drew a line through a circle from one side to the other that does not pass through the center? What if you drew a line outside a circle that touched the circle at one point? What would you call these lines you drew?
  ::万一您从一面到另一面画一条线, 从一面到另一面画一条线, 却不通过中间线呢? 如果您在一端触碰圆的圆外画一条线呢? 您如何称呼这些线?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

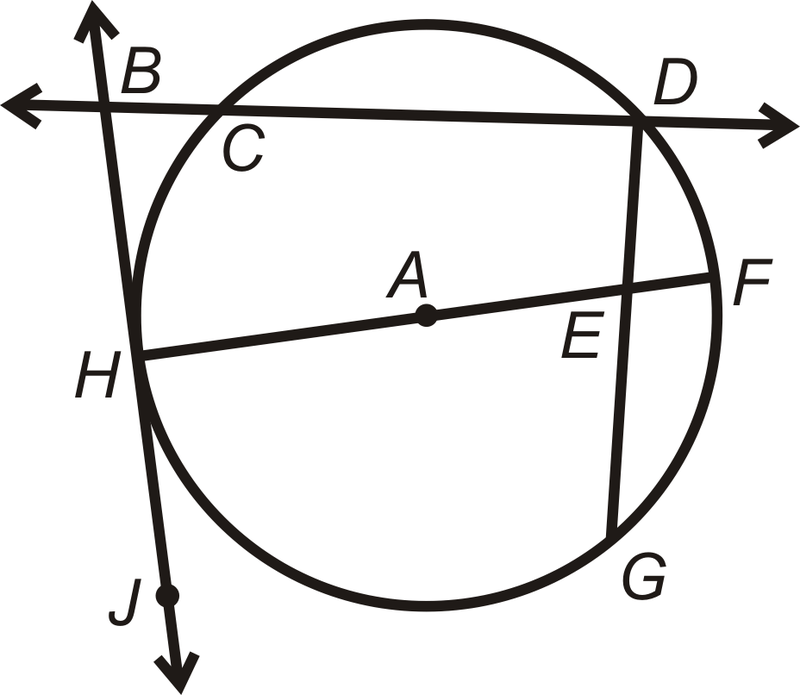
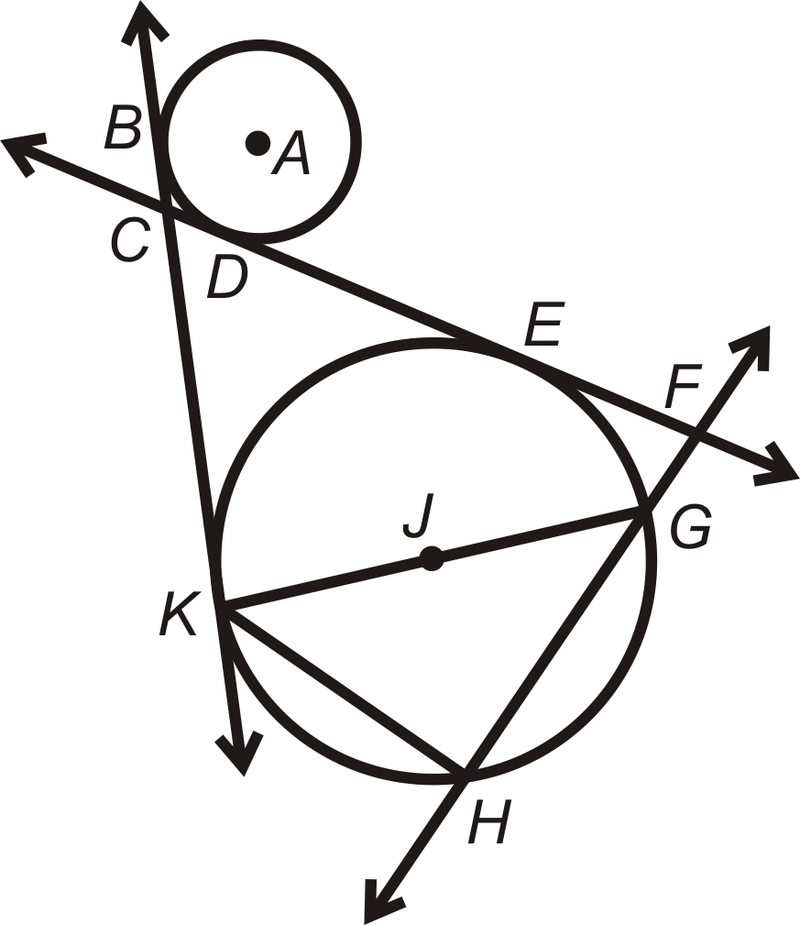
  播放段落

  Find the parts of $\begin{align*}\bigodot A\end{align*}$ that best fit each description.
  ::找到ZAA最符合每个描述的部分。

  

  播放段落
  1. A radius
     ::A半径

  播放段落

    $\begin{align*}\overline{HA}\end{align*}$ or $\begin{align*}\overline{AF}\end{align*}$
  ::# # 或 # # # # # h # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

  播放段落
  2. A chord
     ::和弦和弦

  播放段落

    $\begin{align*}\overline{CD}, \ \overline{HF}\end{align*}$ , or $\begin{align*}\overline {DG}\end{align*}$
  ::d, hH, 或

  播放段落
  3. A tangent line
     ::一条正切线

  播放段落

    $\begin{align*}\overleftrightarrow{BJ}\end{align*}$
  ::# BJ # # BJ # # BJ # # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ # BJ #

  播放段落
  4. A point of tangency
     ::某一具体点

  播放段落

   Point $\begin{align*}H\end{align*}$
  ::H点点

  播放段落
  5. A diameter
     ::A直径

  播放段落

    $\begin{align*}\overline{HF}\end{align*}$
  ::- HF - HF - - - HF - - - - - - - - - - - - - - - - - - - - - - - -

  播放段落
  6. A secant
     ::A 秒数

  播放段落

    $\begin{align*}\overleftrightarrow{BD}\end{align*}$
  ::{BD_BD_BD_BD_BD_BD_BD_BD_BD_BD_BD_BD_BD

  播放段落

  Example 2
  ::例2

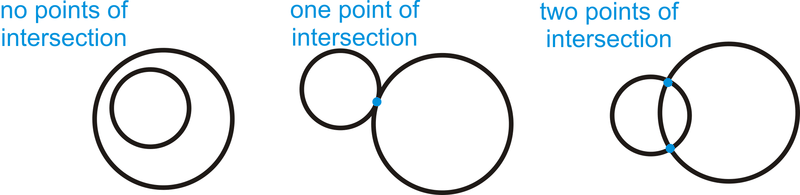
  播放段落

  Draw an example of how two circles can intersect with no, one and two points of intersection . You will make three separate drawings.
  ::绘制一个示例, 显示两个圆圈如何交叉, 交叉点为空、 1 和 2 个。 您将绘制三个独立的图纸 。

  

  播放段落

  Example 3
  ::例3

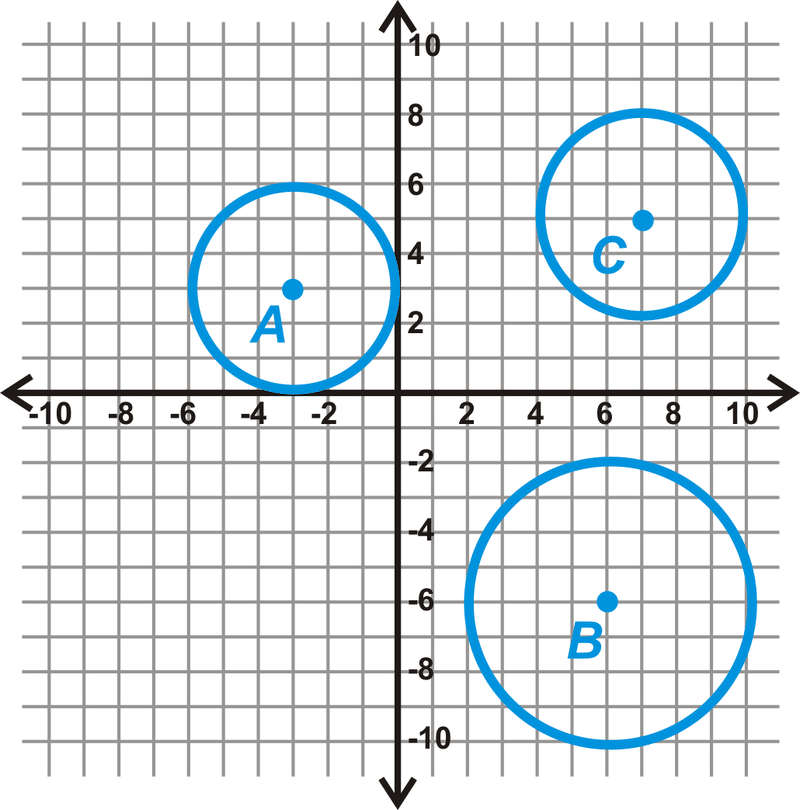
  播放段落

  Determine if any of the following circles are congruent .
  ::确定以下圆圈中是否有相同圆。

  

  播放段落

  From each center, count the units to the outer rim of the circle. It is easiest to count vertically or horizontally. Doing this, we have:
  ::从每个中心, 从每个中心, 计数单位到圆的外边缘。 很容易垂直或水平地计数。 这样做, 我们得到 :

  播放段落

  $$\begin{align*}\text{Radius of} \ \bigodot A & = 3 \ units\\ \text{Radius of} \ \bigodot B & = 4 \ units\\ \text{Radius of} \ \bigodot C & = 3 \ units\end{align*}$$
  ::A=3 单位Radius= B=4 单位Radius= C=3 单位

  播放段落

  From these measurements, we see that $\begin{align*}\bigodot A \cong \bigodot C\end{align*}$ .
  ::从这些测量中,我们看到了AAC。

  播放段落

  Notice the circles are congruent. The lengths of the radii are equal.
  ::注意圆圈是相同的 弧度长度相等

  播放段落

  Example 4
  ::例4

  播放段落

  Is it possible to have a line that intersects a circle three times? If so, draw one. If not, explain.
  ::是否可能有一个横线将圆交叉三次? 如果是,请绘制一条。如果没有,请解释。

  播放段落

  It is not possible. By definition, all lines are straight . The maximum number of times a line can intersect a circle is twice.
  ::不可能。 根据定义, 所有的线条都是直线。 一条线最多能交叉圆的倍数是两次 。

  播放段落

  Example 5
  ::例5

  播放段落

  Are all circles similar ?
  ::所有圆圈都相似吗?

  播放段落

  Yes. All circles are the same shape, but not necessarily the same size, so they are similar.
  ::是的,所有圆圈的形状都一样,但不一定大小相同,因此它们相似。

  播放段落

  Review
  ::回顾

  播放段落

  Determine which term best describes each of the following parts of $\begin{align*}\bigodot P\end{align*}$ .
  ::确定哪个术语最能说明 " +P " 的以下每一部分。

  

  播放段落
  1. $\begin{align*}\overline{KG}\end{align*}$
     :K) (K)
  播放段落
  2. $\begin{align*}\overleftrightarrow{FH}\end{align*}$
     ::芬 芬 华
  播放段落
  3. $\begin{align*}\overline{KH}\end{align*}$
     :KH)
  播放段落
  4. $\begin{align*}E\end{align*}$
     ::英 英 英
  播放段落
  5. $\begin{align*}\overleftrightarrow{BK}\end{align*}$
     ::# BK # # BK # # BK # # BK #
  播放段落
  6. $\begin{align*}\overleftrightarrow{CF}\end{align*}$
     ::CF CF CF CF CF CF CF CF CF CF CF CF CF CF
  播放段落
  7. $\begin{align*}A\end{align*}$
     ::A A A
  播放段落
  8. $\begin{align*}\overline{JG}\end{align*}$
     ::# 城 # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
  播放段落
  9. What is the longest chord in any circle?
     ::圆圈中最长的和弦是什么?

  播放段落

  Use the graph below to answer the following questions.
  ::使用下图回答下列问题。

  播放段落
  10. Find the radius of each circle.
      ::查找每个圆的半径。
  播放段落
  11. Are any circles congruent? How do you know?
      ::圆圈是否一致?
  播放段落
  12. $\begin{align*}\bigodot C\end{align*}$ and $\begin{align*}\bigodot E\end{align*}$ are externally tangent. What is $\begin{align*}CE\end{align*}$ ?
      ::C和E是外部相切的 CE是什么?
  播放段落
  13. Find the equation of $\begin{align*}\overline{CE}\end{align*}$ .
      
      
      ::找到CE的方程式

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源