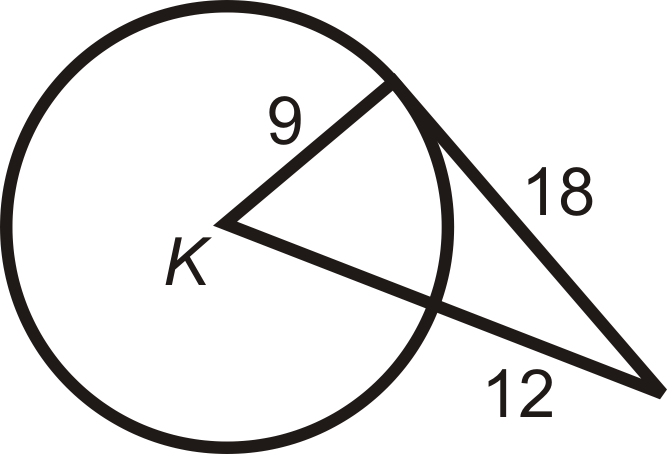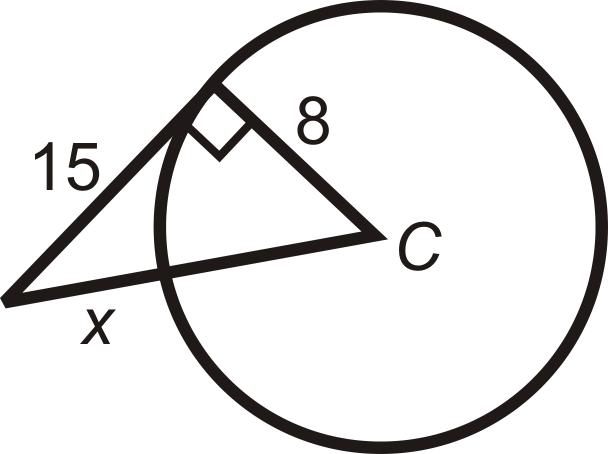9.2 切线线
章节大纲
-
Tangent Line Theorems
::切切线线定理There are two important theorems about tangent lines.
::有两条重要的理论 是关于正切线的1. Tangent to a Circle Theorem : A line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency .
::1. 圆形定理的切线:线与圆形的切线相切,条件是且只有在线线与划入正切点的半径垂直。↔ B C is tangent at point B if and only if ↔ B C ⊥ ¯ A B .
::BC在B点是相切的,如果,而且只有在BCABA的情况下。This theorem uses the words “if and only if,” making it a biconditional statement , which means the converse of this theorem is also true.
::这一定理使用了“如果而且只有在”等字,使该定理成为两条条件的声明,这意味着该定理的反义也是真实的。2. Two Tangents Theorem: If two tangent segments are drawn to one circle from the same external point, then they are congruent .
::2. 两个切线定理:如果从同一个外部点将两个正切区段划为一个圆形,那么它们就是相同的。¯ B C and ¯ D C have C as an endpoint and are tangent; ¯ B C ≅ ¯ D C .
::BC和CC是终点,相切; BC和C是终点; BC。What if a line were drawn outside a circle that appeared to touch the circle at only one point? How could you determine if that line were actually a tangent?
::如果一条线是在似乎只触及圆点的圆外划出的,那又如何?你如何确定这条线是否实际是相左线呢?Examples
::实例Example 1
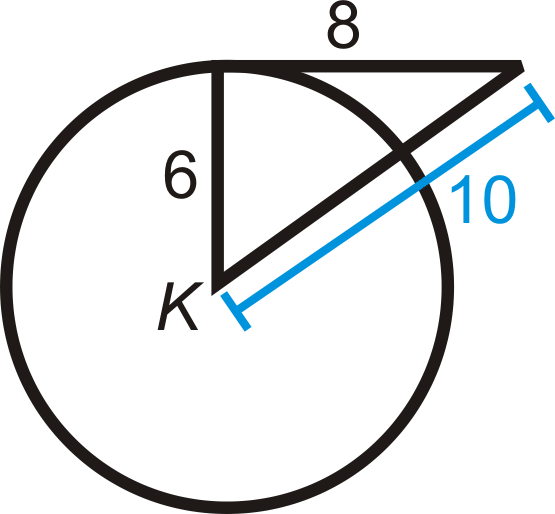
::例1Determine if the triangle below is a right triangle .
::确定下方三角形是否为右三角形。Use . 4 √ 10 is the longest side, so it will be c .
::使用 。 410 是最长的一面, 所以这将是 c 。Does 8 2 + 10 2 = ( 4 √ 10 ) 2 ? 64 + 100 ≠ 160
::82+102=(410)2?64+100=160△ A B C is not a right triangle. From this, we also find that ¯ C B is not tangent to ⨀ A .
::ABC不是一个正确的三角形,Example 2
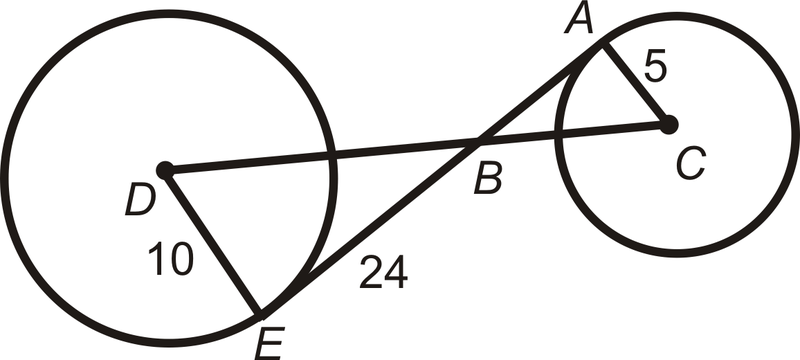
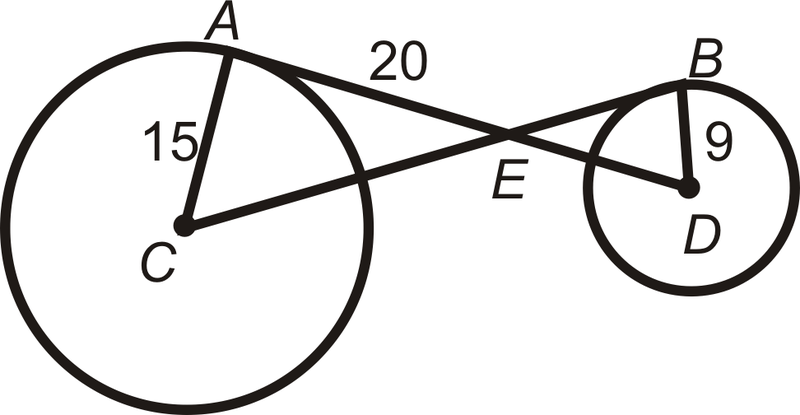
::例2If D and C are the centers and A E is tangent to both circles, find D C .
::如果D和C是中心 而AE对双方都不同 找到DC¯ A E ⊥ ¯ D E and ¯ A E ⊥ ¯ A C and △ A B C ∼ △ D B E by .
::和AEAC和ABCDBE的到来。To find D B , use the Pythagorean Theorem.
::找到DB,使用毕达哥里安神话10 2 + 24 2 = D B 2 100 + 576 = 676 D B = √ 676 = 26
::102+242=DB2100+576=676DB=676=26To find B C , use similar triangles . 5 10 = B C 26 ⟶ B C = 13. D C = D B + B C = 26 + 13 = 39
::要找到 BBC, 请使用类似的三角形 。 510= BC26BC=13。 DC=DB+BC=26+13=39Example 3
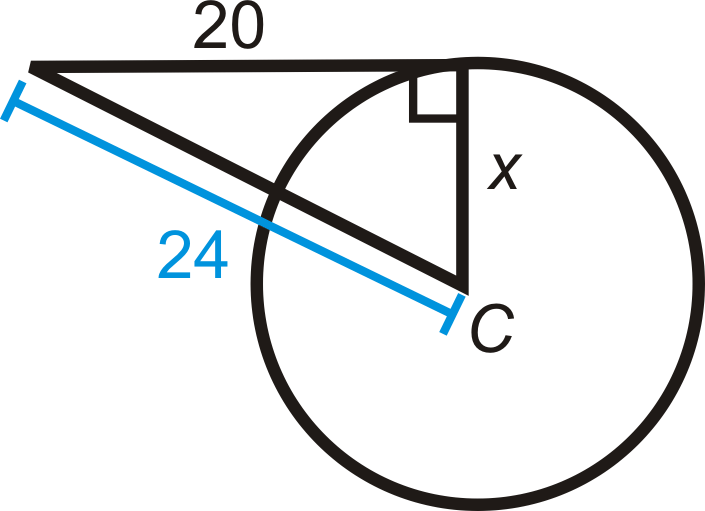
::例3¯ C B is tangent to ⨀ A at point B . Find A C . Reduce any radicals.
::CB与B点的A相切 找到AC 减少任何激进分子¯ C B is tangent, so ¯ A B ⊥ ¯ C B and △ A B C a right triangle. Use the Pythagorean Theorem to find A C .
::CB是正切的,所以ABC和ABC是右三角。使用毕达哥伦理论来找到AC。5 2 + 8 2 = A C 2 25 + 64 = A C 2 89 = A C 2 A C = √ 89
::52+82=AC225+64=AC289=AC2AC_89Example 4
::例4Using the answer from Example A above, find D C in ⨀ A . Round your answer to the nearest hundredth.
::使用上文例A的回答, 请在 QA 中找到 DC。 将您的回答回溯到最近的第一百次 。D C = A C − A D D C = √ 89 − 5 ≈ 4.43
::DC=AC-ADDC 89-54.43Example 5
::例5Find the perimeter of △ A B C .
::找到ABC的周边A E = A D , E B = B F , and C F = C D . Therefore, the perimeter of △ A B C = 6 + 6 + 4 + 4 + 7 + 7 = 34 .
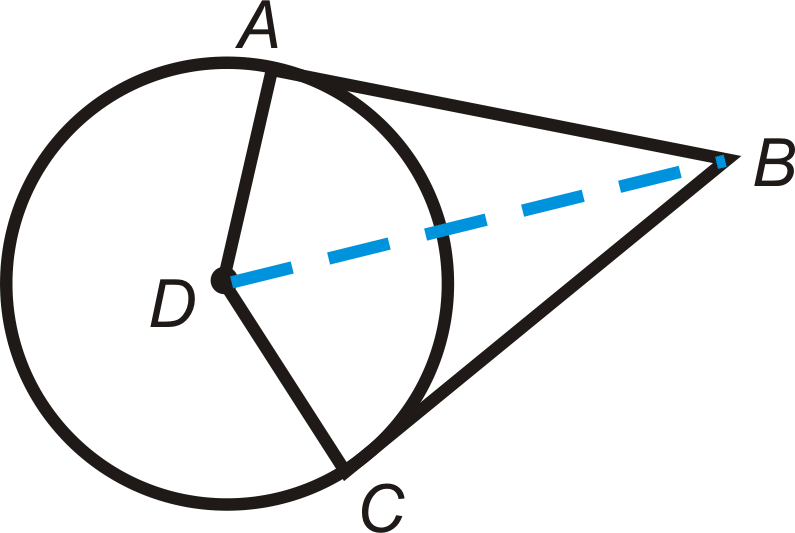
::AE=AD,EB=BF,CF=CD。因此,ZABC=6+6+4+4+4+7+7=34的周界。⨀ G is inscribed in △ A B C . A circle is inscribed in a polygon if every side of the polygon is tangent to the circle.
::ABC 中输入了 G。如果多边形的每一面与圆正切,则在多边形中输入一个圆。Review
::回顾Determine whether the given segment is tangent to ⨀ K .
::确定给定的区段是否正切到 _K 。Find the value of the indicated length(s) in ⨀ C . A and B are points of tangency. Simplify all radicals.
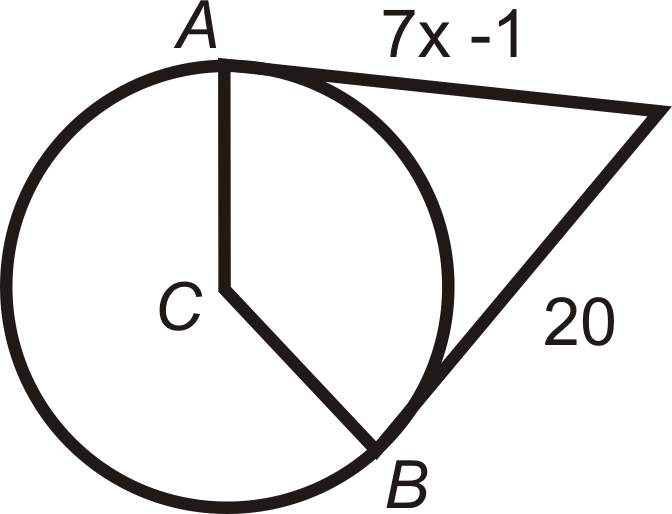
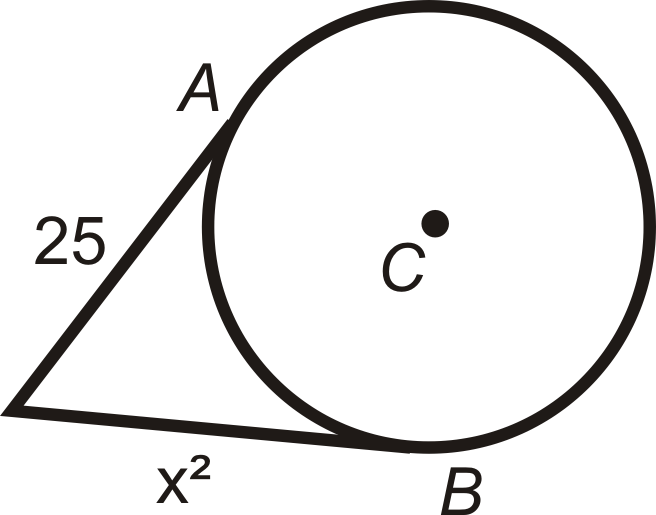
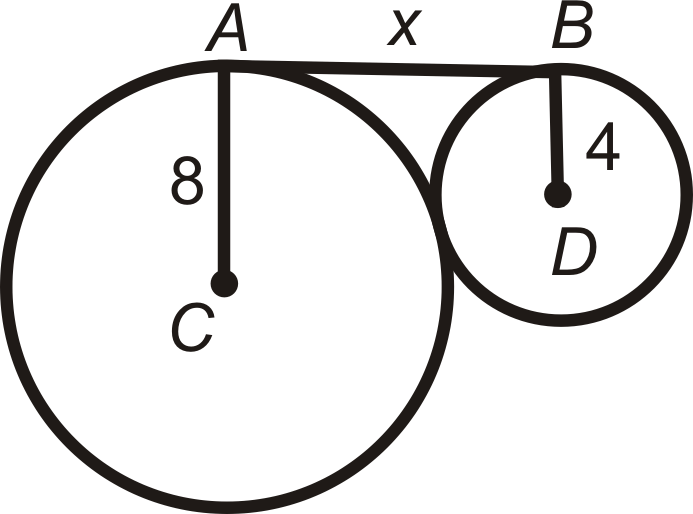
::查找 QC. A 和 B 中标明的长度值是相切点。 简化所有基体 。A and B are points of tangency for ⨀ C and ⨀ D .
::A和B是C和D的切合点。-
Is
△
A
E
C
∼
△
B
E
D
? Why?
::为什么? -
Find
C
E
.
::找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE,找CE -
Find
B
E
.
::寻找BE。 -
Find
E
D
.
::寻找ED。 -
Find
B
C
and
A
D
.
::找到BC和AD
⨀ A is inscribed in B D F H .
::A以BDFH登记。-
Draw a circle inscribed in a square. If the radius of the circle is 5, what is the perimeter of the square?
::绘制在方形中标注的圆。如果圆的半径是 5,则方形的周界是什么? -
Can a circle be inscribed in a rectangle? If so, draw it. If not, explain.
::一个圆可以嵌入矩形吗?如果可以,请绘制。如果没有,请解释。 -
Draw a triangle with two sides tangent to a circle, but the third side is not.
::绘制三角形,将两面切换为圆,但第三面不是。 -
Can a circle be inscribed in an obtuse triangle? If so, draw it. If not, explain.
::一个圆可以刻在隐形三角形中吗? 如果是, 请绘制它。 如果没有, 请解释 。 -
Fill in the blanks in the proof of the Two Tangents Theorem.
::填满两个丹根人理论的 证据中的空白
Given : ¯ A B and ¯ C B with points of tangency at A and C . ¯ A D and ¯ D C are radii.
::参考:A.C.A.A.A.A.和C.C.C.C.Prove : ¯ A B ≅ ¯ C B
::证明:Statement Reason 1. 1. 2. ¯ A D ≅ ¯ D C 2. 3. ¯ D A ⊥ ¯ A B and ¯ D C ⊥ ¯ C B 3. 4. 4. Definition of perpendicular lines 5. 5. Connecting two existing points 6. △ A D B and △ D C B are right triangles 6. 7. ¯ D B ≅ ¯ D B 7. 8. △ A B D ≅ △ C B D 8. 9. ¯ A B ≅ ¯ C B 9. -
Fill in the blanks, using the proof from #21.
-
A
B
C
D
is a _____________ (type of quadrilateral).
::ABCD是一种(四边形类型)。 -
The line that connects the ___________ and the external point
B
__________
∠
A
B
C
.
::连接 和 外部点 B ABC 的线条。
::填入空白, 使用 # 21 的证明 。 ABCD 是 (四边形的类型) 。 连接 和 外部点 B ABC 的线 。 -
A
B
C
D
is a _____________ (type of quadrilateral).
-
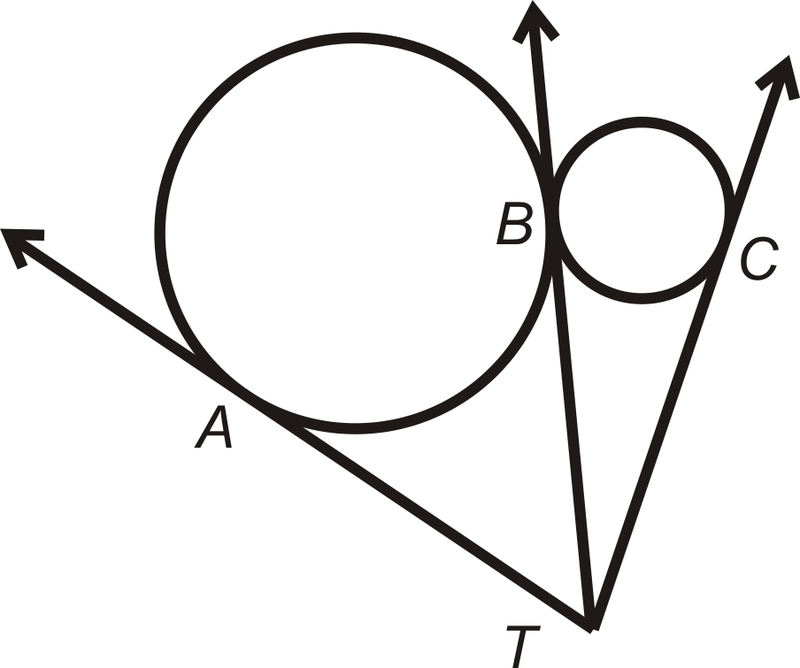
Points
A
,
B
,
and
C
are points of tangency for the three tangent circles.
Explain
why
¯
A
T
≅
¯
B
T
≅
¯
C
T
.
::A点、B点和C点是三个相近的圈子的相切点。
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。Resources
::资源 -