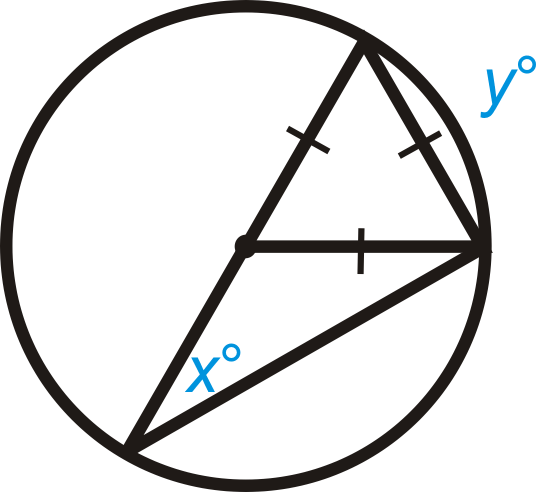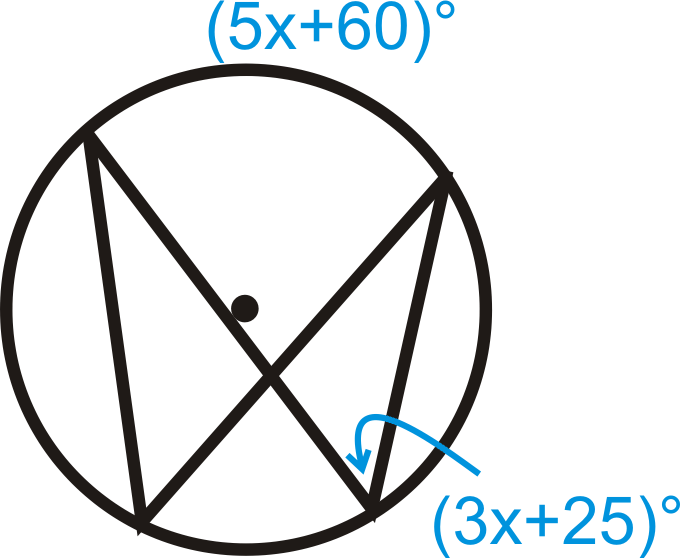9.5 圆形中的归属角
章节大纲
-
Inscribed Angles in Circles
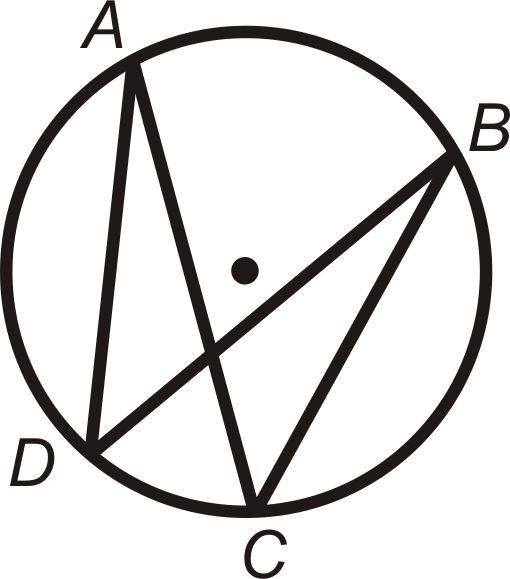
::圆圆中指定的角An inscribed angle is an angle with its vertex on the circle and whose sides are chords. The intercepted arc is the arc that is inside the inscribed angle and whose endpoints are on the angle. The vertex of an inscribed angle can be anywhere on the circle as long as its sides intersect the circle to form an intercepted arc.
::刻入角是圆上带有顶点的角,其侧面是和弦。 截取弧是刻入角内的弧, 其端点在角上。 刻入角的顶点可以是圆的任何地方, 只要其侧面交叉圆以形成被截取的弧。The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of its intercepted arc.
::所描述的角定理称,一个刻着角的测量量是其截取弧的测量量的一半。m ∠ A D C = 1 2 m ^ A C and m ^ A C = 2 m ∠ A D C
::mADC=12米AC和mAAC=2米ADCInscribed angles that intercept the same arc are congruent . This is called the Congruent Inscribed Angles Theorem and is shown below.
::截取相同弧的指定角度是相容的。 这个角度被称为“ 相连接的相角定理 ” , 显示在下面 。∠ A D B and ∠ A C B intercept ^ A B , so m ∠ A D B = m ∠ A C B . Similarly, ∠ D A C and ∠ D B C intercept ^ D C , so m ∠ D A C = m ∠ D B C .
::亚银和ACB拦截AB,所以m亚银=mACB。 类似地,DAC和DB拦截DC,所以mDAC=mDBC。An angle intercepts a semicircle if and only if it is a right angle ( Semicircle Theorem ). Anytime a right angle is inscribed in a circle, the endpoints of the angle are the endpoints of a diameter and the diameter is the hypotenuse .
::角截取半圆圈,如果且只有在右角( 细胞理论) 的情况下才拦截半圆圈。 当右角被刻在一个圆圈中时, 角的终点是直径的端点, 直径是下限 。What if you had a circle with two chords that share a common endpoint ? How could you use the arc formed by those chords to determine the measure of the angle those chords make inside the circle?
::如果你有一个圆形,有两个和弦,两个和弦具有共同的终点呢?你如何使用这些和弦形成的弧来决定这些和弦在圆内所产生角的大小?Examples
::实例Example 1
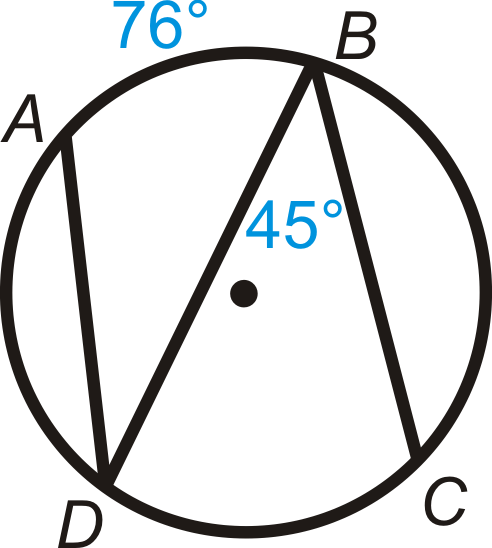
::例1Find m ^ D C and m ∠ A D B .
::找到MDC和MADB。From the Inscribed Angle Theorem:
::是从预定的角定理中摘取的:m ^ D C = 2 ⋅ 45 ∘ = 90 ∘ m ∠ A D B = 1 2 ⋅ 76 ∘ = 38 ∘
::mDC=24590mADB=127638Example 2
::例2Find m ∠ A D B and m ∠ A C B .
::寻找mADB和mACB。The intercepted arc for both angles is ^ A B . Therefore,
::两个角度被截取的弧为 AB。因此,m ∠ A D B = 1 2 ⋅ 124 ∘ = 62 ∘ m ∠ A C B = 1 2 ⋅ 124 ∘ = 62 ∘
::1212462771212462Example 3
::例3Find m ∠ D A B in ⨀ C .
::找到在C的 mDAB 。C is the center , so ¯ D B is a diameter. ∠ D A B 's endpoints are on the diameter, so the central angle is 180 ∘ .
::C是中枢,所以DB是直径。“DAB”的终点在直径上,所以中角是180。m ∠ D A B = 1 2 ⋅ 180 ∘ = 90 ∘ .
::mDAB=12 -180 -90\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\DAB=12 -180Example 4
::例4Fill in the blank: An inscribed angle is ____________ the measure of the intercepted arc.
::填入空白: 刻入角度是 被截取弧的度量 。half
::一半一半Example 5
::例5Fill in the blank: A central angle is ________________ the measure of the intercepted arc.
::填空: 中心角度是 被截取弧的度量 。equal to
::等于Review
::回顾Fill in the blanks.
::填满空白。-
An angle inscribed in a ________________ is
90
∘
.
::在 中刻入的角是 90 。 -
Two inscribed angles that intercept the same arc are _______________.
::截取相同弧的两个刻入角度为 。 -
The sides of an inscribed angle are ___________________.
::所刻角度的侧面是 _____________________________________________________________________________________________________________ -
Draw inscribed angle
∠
J
K
L
in
⨀
M
. Then draw central angle
∠
J
M
L
. How do the two angles relate?
::绘制在 \ \ \ \ \ \ JKL 中刻的角 \ JKL 。 然后绘制中心角 \ JML 。 两个角度的关系如何 ?
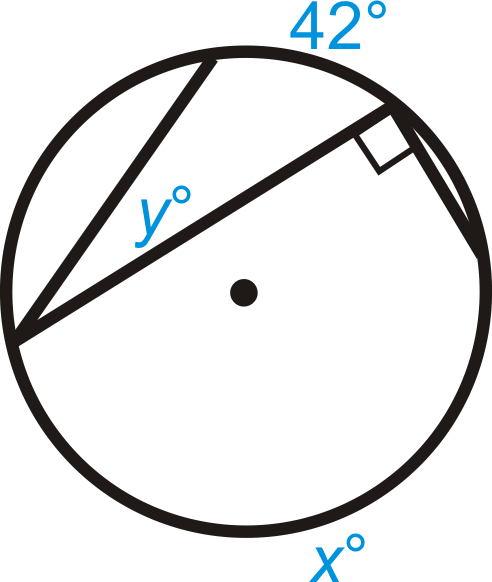
Find the value of x and/or y in ⨀ A .
::在 {A} 中查找 x 和/或 y 值。Solve for x .
::解决x。-
-
-
-
-
Fill in the blanks of the Inscribed Angle Theorem proof.
::填入给定的角定理证据的空白 。
Given : Inscribed ∠ A B C and diameter ¯ B D
::给定值: ABC和直径=BDProve : m ∠ A B C = 1 2 m ^ A C
::证明: mABC=12mACStatement Reason 1. Inscribed ∠ A B C and diameter ¯ B D
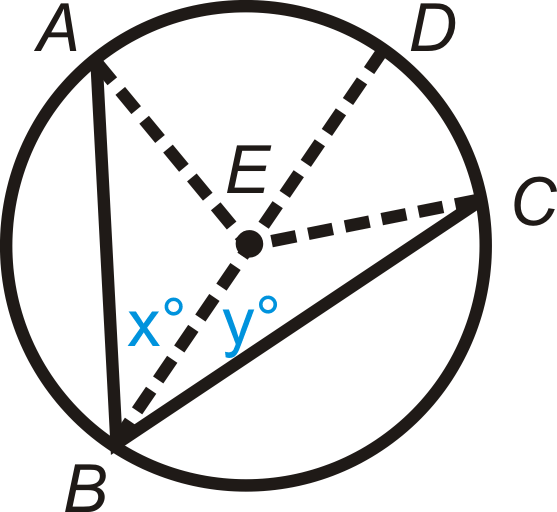
::1. 说明的 ABC 和直径 `BDm ∠ A B E = x ∘ and m ∠ C B E = y ∘
::mABE=x和mCBE=y1. 2. x ∘ + y ∘ = m ∠ A B C 2. 3. 3. All radii are congruent 4. 4. Definition of an isosceles triangle 5. m ∠ E A B = x ∘ and m ∠ E C B = y ∘ 5. 6. m ∠ A E D = 2 x ∘ and m ∠ C E D = 2 y ∘ 6. 7. m ^ A D = 2 x ∘ and m ^ D C = 2 y ∘ 7. 8. 8. Arc Addition Postulate 9. m ^ A C = 2 x ∘ + 2 y ∘ 9. 10. 10. Distributive PoE 11. m ^ A C = 2 m ∠ A B C 11. 12. m ∠ A B C = 1 2 m ^ A C 12. Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
An angle inscribed in a ________________ is
90
∘
.