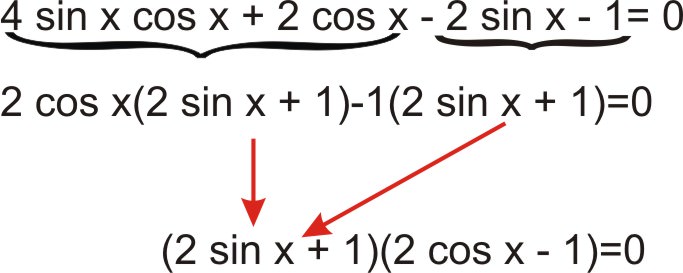Course: 3.4 采用保理法的三角等量

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 采用保理法的三角等量

Collapse Expand
采用保理法的三角等量
Solving trig equations is an important process in mathematics. Quite often you'll see powers of trigonometric functions and be asked to solve for the values of the variable which make the equation true. For example, suppose you were given the trig equation
::解决三角方程式是数学中一个重要的过程。通常你会看到三角函数的力量, 并被要求解答使方程式真实的变量值。例如, 假设您得到了三角方程式的话。

$\begin{aligned} 2 \sin x \cos x = \cos x \end{aligned}$
::2sin xxcosx=cosxx 2sin xxxxxx =cosxxx

Trigonometric Equations Using Factoring
::采用保理法的三角等量

You have no doubt had experience with factoring . You have probably factored equations when looking for the possible values of some variable, such as "x". It might interest you to find out that you can use the same factoring method for more than just a variable that is a number. You can factor trigonometric equations to find the possible values the function can take to satisfy an equation.
::您无疑有计算因素的经验。您在寻找某些变量( 如“ x ” ) 的可能值时, 可能已经应用了计算因素方程。您可能会感兴趣地发现, 您可以使用相同的计算方法, 而不是仅仅对一个数字变量使用同样的计算方法。您可以用三角方程来找到函数满足等式所需的可能值。

Algebraic skills like factoring and substitution that are used to solve various equations are very useful when . As with algebraic expressions, one must be careful to avoid dividing by zero during these maneuvers.
::用于解析各种方程式的乘数和替代等代数技能非常有用。与代数表达式一样,人们必须小心避免在这些动作中以零除法。

Solving for Unknown Values
::解决未知值

1. Solve $\begin{aligned} 2 \sin^{2} x - 3 \sin x + 1 = 0 \end{aligned}$ for $\begin{aligned} 0 < x \leq 2 π \end{aligned}$ .
::1. 0<x%2x-3sinx+1=0,解决2sin2x-3sinx+1=0。

$\begin{aligned} 2 \sin^{2} x - 3 \sin x + 1 = 0 Factor this like a quadratic equation \\ (2 \sin x - 1) (\sin x - 1) = 0 \\ ↓ ↘ \\ 2 \sin x - 1 = 0 or \sin x - 1 = 0 \\ 2 \sin x = 1 \sin x = 1 \\ \sin x = \frac{1}{2} x = \frac{π}{2} \\ x & = \frac{π}{6} and x = \frac{5 π}{6} \end{aligned}$

::2sin2x- 3sinx+1=0 矩形方程式( 2sinx-1)( sinx- 1) =0 2sinx-1=0or sinx- 1=0 2sinx=1 sinx=1 sinx=1 sinx=1 sinx=12 x2x6 和 x=5}

2. Solve $\begin{aligned} 2 \tan x \sin x + 2 \sin x = \tan x + 1 \end{aligned}$ for all values of $\begin{aligned} x \end{aligned}$ .
::2. 为x的所有值解决 2tanxsinx+2sinx=tanx+1。

Pull out $\begin{aligned} \sin x \end{aligned}$
::拔出 sinx

There is a common factor of $\begin{aligned} (\tan x + 1) \end{aligned}$
::有一个共同系数(tanx+1)

Think of the $\begin{aligned} - (\tan x + 1) \end{aligned}$ as $\begin{aligned} (- 1) (\tan x + 1) \end{aligned}$ , which is why there is a $\begin{aligned} - 1 \end{aligned}$ behind the $\begin{aligned} 2 \sin x \end{aligned}$ .
::将- (tanx+1) 视为 (-1) (tanx+1) , 这就是为什么 2sinx 后面有 -1 。

3. Solve $\begin{aligned} 2 \sin^{2} x + 3 \sin x - 2 = 0 \end{aligned}$ for all $\begin{aligned} x, [0, π] \end{aligned}$ .
::3. 为所有 x,[0], 解决 2sin2 x+3sinx-2=0。

$\begin{aligned} 2 \sin^{2} x + 3 \sin x - 2 = 0 \to Factor like a quadratic \\ (2 \sin x - 1) (\sin x + 2) = 0 \\ ↙ ↘ \\ 2 \sin x - 1 = 0 \sin x + 2 = 0 \\ \sin x = \frac{1}{2} \sin x = - 2 \\ x & = \frac{π}{6} and x = \frac{5 π}{6} There is no solution because the range of \sin x is [- 1, 1] . \end{aligned}$

::2sin2x+3sinx-2=021(sinx+2)=02sin*x-1=0sinx+2=0sin*x+2=0sinx=12sinx2x6和x=5}没有解决办法,因为sinx的范围是[-1]。

Some trigonometric equations have no solutions. This means that there is no replacement for the variable that will result in a true expression.
::有些三角方程式没有解决方案。这意味着无法替换变量, 从而得出真实表达式。

Examples
::实例

Example 1
::例1

Earlier, you were asked to solve this:
::早些时候,有人要求你解决这个问题:

$\begin{aligned} 2 \sin x \cos x = \cos x \end{aligned}$
::2sin xxcosx=cosxx 2sin xxxxxx =cosxxx

Subtract $\begin{aligned} \cos x \end{aligned}$ from both sides and factor it out of the equation:
::将两侧的cosx 减法, 并将之从等式中除以 :

$\begin{aligned} 2 \sin x \cos x - \cos x = 0 \\ \cos x (2 \sin x - 1) = 0 \end{aligned}$

::2sinxcosx-cosx=0cosx( 2sinx- 1) =0

Now set each factor equal to zero and solve. The first is $\begin{aligned} \cos x \end{aligned}$ :
::现在设定每个系数等于零并解答。第一个系数是 cosx :

$\begin{aligned} \cos x = 0 \\ x = \frac{π}{2}, \frac{3 π}{2} \end{aligned}$

::COsx=0x2,32

And now for the other term:
::现在换句话说:

$\begin{aligned} 2 \sin x - 1 = 0 \\ \sin x = \frac{1}{2} \\ x = \frac{π}{6}, \frac{5 π}{6} \end{aligned}$

::2sinx-1=0sinx=12x6,56

Example 2
::例2

Solve the trigonometric equation $\begin{aligned} 4 \sin x \cos x + 2 \cos x - 2 \sin x - 1 = 0 \end{aligned}$ such that $\begin{aligned} 0 \leq x < 2 π \end{aligned}$ .
::解析三角方程式 4sinxxcosx+2cosx-2sinx-1=0, 等於 0x<2。

Use factoring by grouping.
::通过分组计算使用系数。

$\begin{aligned} 2 \sin x + 1 = 0 or 2 \cos x - 1 = 0 \\ 2 \sin x = - 1 2 \cos x = 1 \\ \sin x = - \frac{1}{2} \cos x = \frac{1}{2} \\ x = \frac{7 π}{6}, \frac{11 π}{6} x = \frac{π}{3}, \frac{5 π}{3} \end{aligned}$

::2sinx+1=0or2cosx-1=02sinx12cosx=1 sinx12cosx=12 x=7}6,11}6x3,53

Example 3
::例3

Solve $\begin{aligned} \tan^{2} x = 3 \tan x \end{aligned}$ for $\begin{aligned} x \end{aligned}$ over $\begin{aligned} [0, π] \end{aligned}$ .
::x 超过 [0] 时, 解决 tan2 = 3tanx 。

$\begin{aligned} \tan^{2} x & = 3 \tan x \\ \tan^{2} x - 3 \tan x & = 0 \\ \tan x (\tan x - 3) & = 0 \\ \tan x & = 0 or \tan x = 3 \\ x & = 0, π x = 1.25 \end{aligned}$

::tan2x=3tanxtan2x-3tanx=0tanx(tanx-3)=0tanx=0ortanx=3x=0,%x=1.25

Example 4
::例4

Find all the solutions for the trigonometric equation $\begin{aligned} 2 \sin^{2} \frac{x}{4} - 3 \cos \frac{x}{4} = 0 \end{aligned}$ over the interval $\begin{aligned} [0, 2 π) \end{aligned}$ .
::在间隔 [0,2] 中找到三角方程 2sin2x4-3cosx4=0 的所有解决方案。

$\begin{aligned} 2 \sin^{2} \frac{x}{4} - 3 \cos \frac{x}{4} = 0 \end{aligned}$
::2 辛2 x4 - 3cos *x4=0

$\begin{aligned} 2 (1 - \cos^{2} \frac{x}{4}) - 3 \cos \frac{x}{4} = 0 \\ 2 - 2 \cos^{2} \frac{x}{4} - 3 \cos \frac{x}{4} = 0 \\ 2 \cos^{2} \frac{x}{4} + 3 \cos \frac{x}{4} - 2 = 0 \\ (2 \cos \frac{x}{4} - 1) (\cos \frac{x}{4} + 2) = 0 \\ ↙ ↘ \\ 2 \cos \frac{x}{4} - 1 = 0 or \cos \frac{x}{4} + 2 = 0 \\ 2 \cos \frac{x}{4} = 1 \cos \frac{x}{4} = - 2 \\ \cos \frac{x}{4} = \frac{1}{2} \\ \frac{x}{4} = \frac{π}{3} or \frac{5 π}{3} \\ x = \frac{4 π}{3} or \frac{20 π}{3} \end{aligned}$

::2(2)-2x4)-3cos2x4=0 2-2cos2x4x4=0 2cos2x4x4x4=0 2cos2x_x4+3cos_x4_x4-2=0(2cos_x4-1)(cos_x4+2)=0Q2cos_x4-1=0orcoos*4+4+2=02cos_x4=02-2cos2x4x4=1cos_x4x4=12x4=12x4}}3o5_3x=4}3或20_3

$\begin{aligned} \frac{20 π}{3} \end{aligned}$ is eliminated as a solution because it is outside of the range and $\begin{aligned} \cos \frac{x}{4} = - 2 \end{aligned}$ will not generate any solutions because $\begin{aligned} - 2 \end{aligned}$ is outside of the range of cosine. Therefore, the only solution is $\begin{aligned} \frac{4 π}{3} \end{aligned}$ .
::203作为一种解决方案被删除,因为它不在范围之内, 并且cosx42不会产生任何解决方案, 因为2- 2 在余弦范围之外。因此, 唯一的解决方案是 43 。

Review
::回顾

Solve each equation for $\begin{aligned} x \end{aligned}$ over the interval $\begin{aligned} [0, 2 π) \end{aligned}$ .
::在间隔[0,2]内为 x 解决每个方程式。

$\begin{aligned} \cos^{2} (x) + 2 \cos (x) + 1 = 0 \end{aligned}$
::COs2(x)+2cos(x)+1=0

$\begin{aligned} 1 - 2 \sin (x) + \sin^{2} (x) = 0 \end{aligned}$
::1-2sin(x)+sin2(x)=0

$\begin{aligned} 2 \cos (x) \sin (x) - \cos (x) = 0 \end{aligned}$
::2cos(x)sin(x)-cos(x)=0

$\begin{aligned} \sin (x) \tan^{2} (x) - \sin (x) = 0 \end{aligned}$
:x)tan2(x)-sin(x)=0

$\begin{aligned} \sec^{2} (x) = 4 \end{aligned}$
::秒2(x)=4

$\begin{aligned} \sin^{2} (x) - 2 \sin (x) = 0 \end{aligned}$
:x) -2sin *(x)=0

$\begin{aligned} 3 \sin (x) = 2 \cos^{2} (x) \end{aligned}$
::3sin(x)=2cos2}(x)

$\begin{aligned} 2 \sin^{2} (x) + 3 \sin (x) = 2 \end{aligned}$
::2sin2(x)+3sin(x)=2

$\begin{aligned} \tan (x) \sin^{2} (x) = \tan (x) \end{aligned}$
::tan(x) sin2(x) =tan(x)

$\begin{aligned} 2 \sin^{2} (x) + \sin (x) = 1 \end{aligned}$
::2sin2(x)+sin(x)=1

$\begin{aligned} 2 \cos (x) \tan (x) - \tan (x) = 0 \end{aligned}$
::2cos(x)tan(x)-tan(x)=0

$\begin{aligned} \sin^{2} (x) + \sin (x) = 2 \end{aligned}$
:x)+sin%(x)=2

$\begin{aligned} \tan (x) (2 \cos^{2} (x) + 3 \cos (x) - 2) = 0 \end{aligned}$
::tan(x)(2cos2)(x)+3cos(x)-2)=0

$\begin{aligned} \sin^{2} (x) + 1 = 2 \sin (x) \end{aligned}$
:x)+1=2sin}(x)

$\begin{aligned} 2 \cos^{2} (x) - 3 \cos (x) = 2 \end{aligned}$
::2cos2(x)-3cos}(x)=2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

采用保理法的三角等量

Trigonometric Equations Using Factoring ::采用保理法的三角等量

Solving for Unknown Values ::解决未知值

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Trigonometric Equations Using Factoring
::采用保理法的三角等量

Solving for Unknown Values
::解决未知值

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)