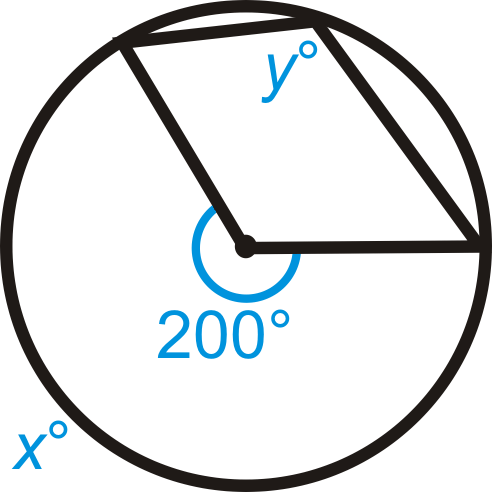9.6 圆圆内规定的四方
章节大纲
-
Inscribed Quadrilaterals in Circles
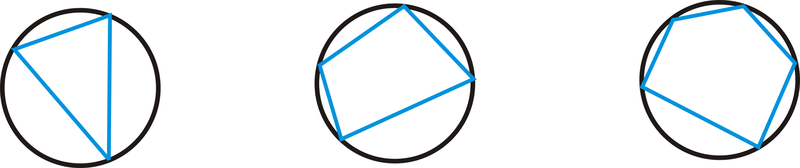
::在圆圆中给定的四方An inscribed polygon is a polygon where every vertex is on the circle , as shown below.
::刻录的多边形是多边形,每个顶点都在圆上,如下文所示。For inscribed quadrilaterals in particular, the opposite angles will always be supplementary.
::特别是对于特定四边形而言,相反的角度总是补充性的。Inscribed Quadrilateral Theorem : A quadrilateral can be inscribed in a circle if and only if the opposite angles are supplementary.
::给定的四方定理:如果而且只有在相反角度是补充的时,四边形才能在圆内标注。If A B C D is inscribed in ⨀ E , then m ∠ A + m ∠ C = 180 ∘ and m ∠ B + m ∠ D = 180 ∘ . Conversely, If m ∠ A + m ∠ C = 180 ∘ and m ∠ B + m ∠ D = 180 ∘ , then A B C D is inscribed in ⨀ E .
::如果 ABCD 在 E 中注册, 那么 mA+mC=180 和 mB+mD=180 。 相反, 如果 mA+mC=180 和 mB+mD=180 , 那么 ABCD 则在 E 中注册 。What if you were given a circle with a quadrilateral inscribed in it? How could you use information about the arcs formed by the quadrilateral and/or the quadrilateral's angle measures to find the measure of the unknown quadrilateral angles?
::如果给您一个圆并刻上四边形呢? 您如何使用由四边形和(或)四边形角度措施形成的弧的信息来找到未知四边形角度的量度?Examples
::实例Example 1
::例1Find the values of the missing variables.
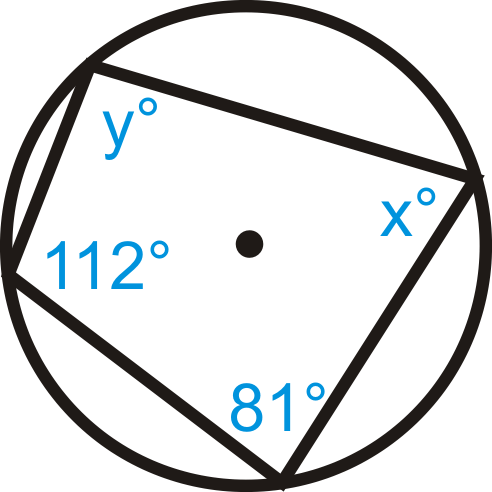
::查找缺失变量的值。x + 80 ∘ = 180 ∘ y + 71 ∘ = 180 ∘ x = 100 ∘ y = 109 ∘
::x+80180y+71180x=100y=109-
z + 93 ∘ = 180 ∘ x = 1 2 ( 58 ∘ + 106 ∘ ) y + 82 ∘ = 180 ∘ z = 87 ∘ x = 82 ∘ y = 98 ∘
::z+93180x=12(58106)y+82180z=87x=82y=98
Example 2
::例2Find x and y in the picture below.
::在下面的图片中查找 x 和 y 。( 7 x + 1 ) ∘ + 105 ∘ = 180 ∘ ( 4 y + 14 ) ∘ + ( 7 y + 1 ) ∘ = 180 ∘ 7 x + 106 ∘ = 180 ∘ 11 y + 15 ∘ = 180 ∘ 7 x = 74 11 y = 165 x = 10.57 y = 15
:7x+1) 105 180(4y+14) (7y+1) 1807x+10618011y+15180187x=7411y=165x=10.57y=15)
Example 3
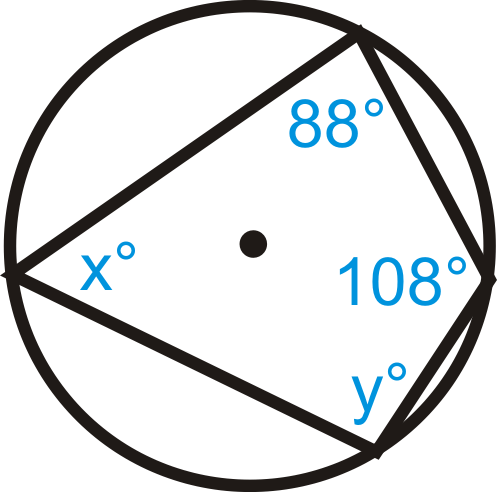
::例3Find the values of x and y in ⨀ A .
::在 A 中查找 x 和 y 的值。Use the Inscribed Quadrilateral Theorem. x ∘ + 108 ∘ = 180 ∘ so x = 72 ∘ . Similarly, y ∘ + 88 ∘ = 180 ∘ so y = 92 ∘ .
::使用给定的四方论。 x108180@ so x=72。 类似地,y88180@y=92。Example 4
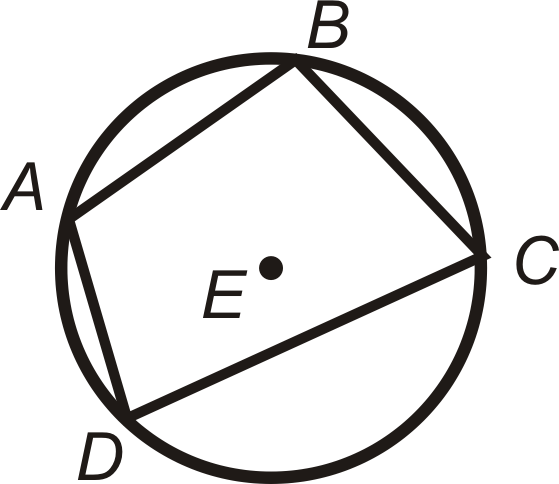
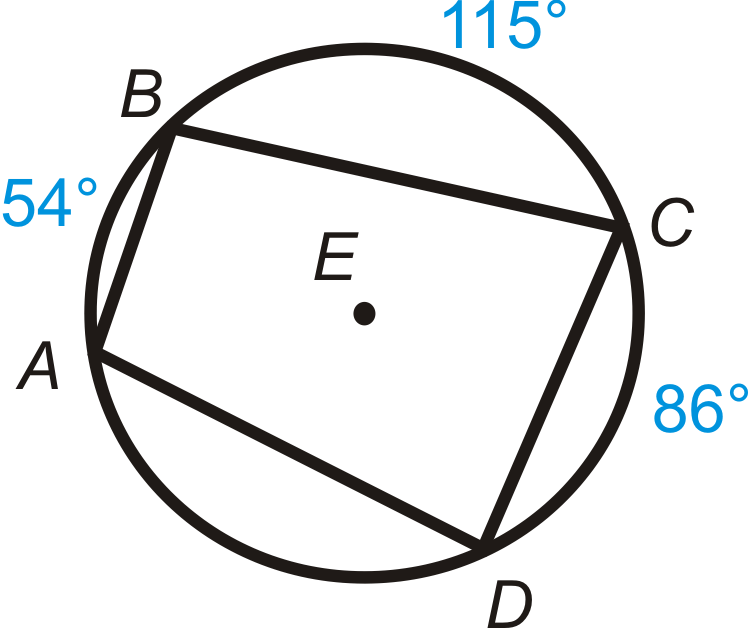
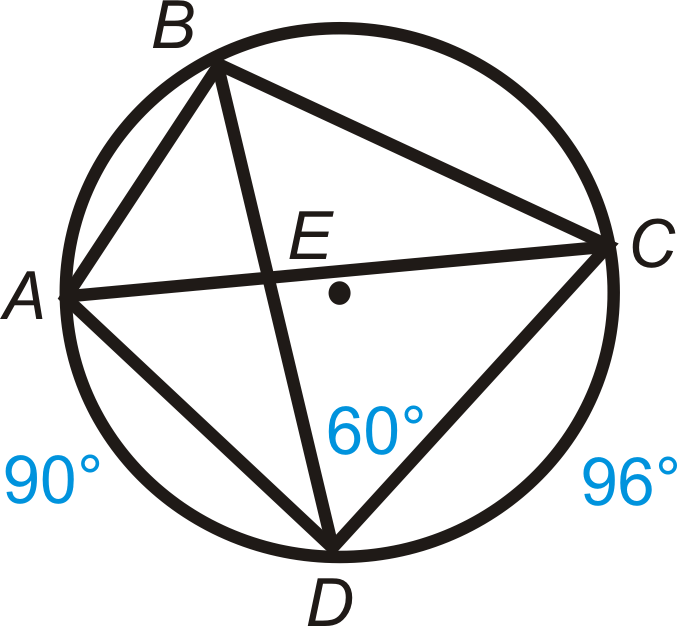
::例4Quadrilateral A B C D is inscribed in ⨀ E . Find m ∠ A , m ∠ B , m ∠ C , and m ∠ D .
::“四边形ABCD”在“E. find mA, mB, mC, and mD.”中刻录。First, note that m ^ A D = 105 ∘ because the complete circle must add up to 360 ∘ .
::首先,请注意 mAD=105,因为整圆必须加到360。m ∠ A = 1 2 m ^ B D = 1 2 ( 115 + 86 ) = 100.5 ∘
::mA=12mBD=12(115+86)=100.5m ∠ B = 1 2 m ^ A C = 1 2 ( 86 + 105 ) = 95.5 ∘
::mB=12mAC=12(86+105)=95.5m ∠ C = 180 ∘ − m ∠ A = 180 ∘ − 100.5 ∘ = 79.5 ∘
::mC=180mA=180100.579.5m ∠ D = 180 ∘ − m ∠ B = 180 ∘ − 95.5 ∘ = 84.5 ∘
::mD=180mB=18095584.5Review
::回顾Fill in the blanks.
::填满空白。-
A
">
(
n
)
_______________ polygon has all its vertices on a circle.
::A多边形在圆上具有全部的顶点。
-
The _____________ angles of an inscribed quadrilateral are ________________.
::一个四边形的 角度是 。
Quadrilateral A B C D is inscribed in ⨀ E . Find:
::E 中刻录了四边形 ABCD。 查找 :-
m
∠
D
B
C
::mDBC -
m
^
B
C
::立方米( mZZZBC) -
m
^
A
B
::m AB -
m
∠
A
C
D
::mACD -
m
∠
A
D
C
::mADC -
m
∠
A
C
B
::mACB( mACB)
Find the value of x and/or y in ⨀ A .
::在 {A} 中查找 x 和/或 y 值。Solve for x .
::解决x。Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -