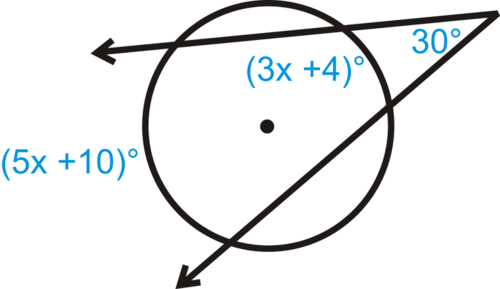9.8 圆外角

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节圆圆外角

  折叠 展开

  圆圆外角

  播放段落

  Here you'll learn how to use the Outside Angle Theorem to solve problems containing angles that are outside a circle.
  ::在这里您将学习如何使用外角定理来解决包含圆外角度的问题。

  播放段落

  Angles Outside a Circle
  ::圆圆外角

  播放段落

  An angle is outside a circle if its vertex is outside the circle and its sides are tangents or . The possibilities are: an angle formed by two tangents, an angle formed by a tangent and a secant , and an angle formed by two secants.
  ::如果一个角度的顶点在圆外,而其侧面是正切或正切的,则该角度在圆外。 可能性是:由两个正切点组成的角,由正切点和片断点组成的角,以及由两个偏差组成的角。

  播放段落

  Outside Angle Theorem : The measure of an angle formed by two secants, two tangents, or a secant and a tangent from a point outside the circle is half the difference of the measures of the intercepted arcs.
  ::角外定理 : 由两个秒、两个切线或一个断线和正切线组成的角在圆外某个点的测量值是被截取弧的测量值的一半。

  

  播放段落

  $\begin{align*}m\angle D = \frac{m\widehat{EF}-m\widehat{GH}}{2}\end{align*}$ , $\begin{align*}m\angle L =\frac{m\widehat{MPN}-m\widehat{MN}}{2}\end{align*}$ , $\begin{align*}m\angle Q =\frac{m\widehat{RS}-m\widehat{RT}}{2}\end{align*}$
  ::mD=mEF-mGH2,mL=mMPN-mMN2,mRS-mRT2

  播放段落

  What if you were given a circle with either two secants, two tangents, or one of each that share a common point outside the circle? How could you use the measure of the arcs formed by those circle parts to find the measure of the angle they make outside the circle? 
  ::如果给您一个圆形, 包括两个空格, 两个正切点, 或者每一个在圆外有一个共同点的圆形呢? 您如何使用这些圆形部分所形成的弧的量度来找到它们在圆外所设定角的量度 ?

  播放段落

  Review
  ::回顾

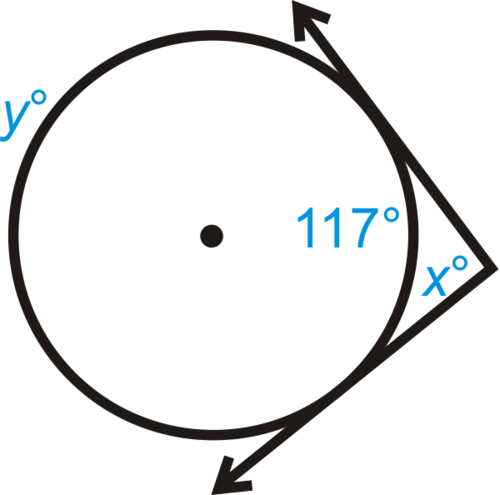
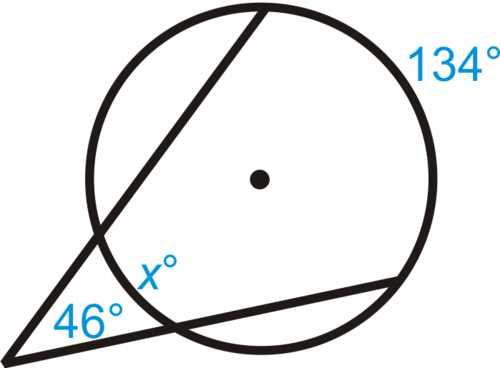
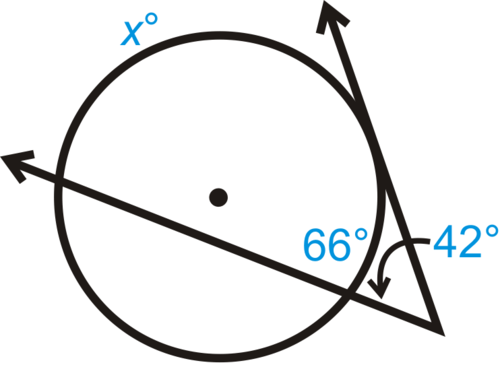
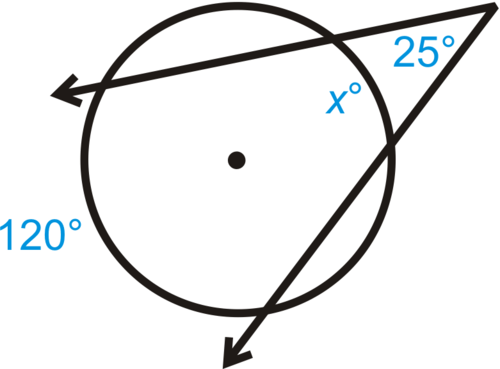
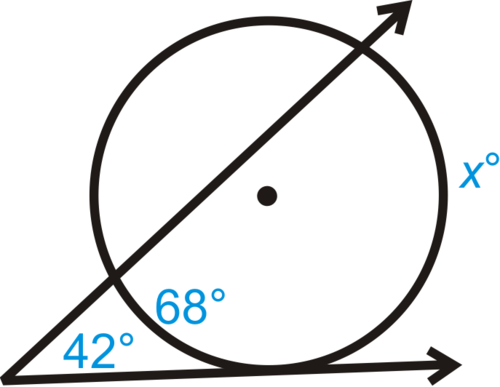
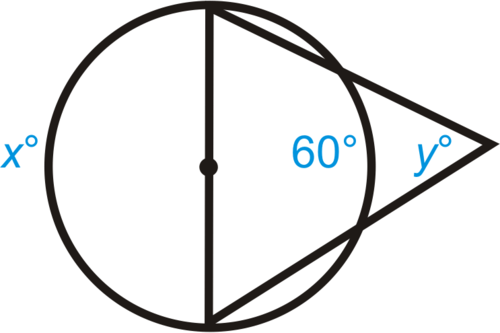
  播放段落

  Find the value of the variables in each diagram below.
  ::在下图中查找变量的值。

  1. 

  2. 

  3. 

  4. 

  5. 

  6. 

  7. 

  8. 

  播放段落
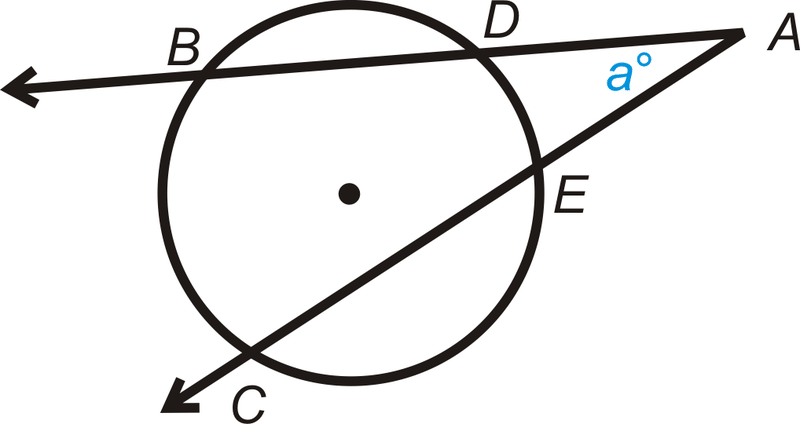
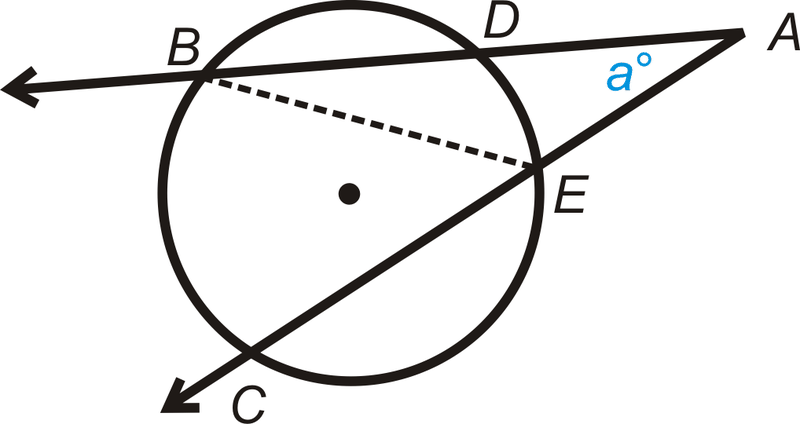
  9. Fill in the blanks of the proof for the Outside Angle Theorem.
     
     
     Given : Secant rays $\begin{align*}\overrightarrow{AB}\end{align*}$ and $\begin{align*}\overrightarrow{AC}\end{align*}$
     Prove : $\begin{align*}m\angle a = \frac{1}{2} \left (m\widehat{BC}-m\widehat{DE} \right )\end{align*}$  
     ::填入外角定理的空白。 根据: secant rays AB 和 AC Prove: ma=12( mBC- mDE)

  Statement	Reason
  1. Intersecting secants $\begin{align*}\overrightarrow{AB}\end{align*}$ and $\begin{align*}\overrightarrow{AC}\end{align*}$ .
  播放段落 2. Draw $\begin{align*}\overline{BE}\end{align*}$ . ::2. 划线。	Construction
  3. $\begin{align*}m\angle BEC=\frac{1}{2} m\widehat{BC}\!\\ m\angle DBE=\frac{1}{2} m\widehat{DE}\end{align*}$
  5. $\begin{align*}m\angle a+m\angle DBE=m\angle BEC\end{align*}$
  6.	Subtraction PoE
  7.	Substitution
  8. $\begin{align*}m\angle a=\frac{1}{2} \left (m\widehat{BC}-m\widehat{DE} \right )\end{align*}$

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。