Course: 3.6 余弦和差异公式

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 余弦和差异公式

Collapse Expand
余弦和差异公式
While playing a board game with friends, you are using a spinner like this one:
::在和朋友玩棋盘游戏时, 你用的是这样的旋翼人:

When you tap the spinner with your hand, it rotates $\begin{align*}110^\circ\end{align*}$ . However, at that moment, someone taps the game board and the spinner moves back a little to $\begin{align*}80^\circ\end{align*}$ . One of your friends, who is a grade above you in math, starts talking to you about trig functions.
::当你用手敲打旋转器时,它会旋转110。然而,在那个时候,有人敲打游戏板,旋转器会回移到80。你的一位朋友,在数学上比你高一级,开始和你谈论三角函数。

"Do you think you can calculate the cosine of the difference between those angles?" he asks.
::“你认为你能计算出这些角度之间的差异的余弦吗?”他问:

"Hmm," you reply. "Sure. I think it's just $\begin{align*}\cos (110^\circ - 80^\circ) = \cos 30^\circ\end{align*}$ ."
::"嗯,"你回答。 "当然,我想这只是cos(11080) =cos30。"

Your friend smiles. "Are you sure?" he asks.
::你的朋友笑着说 "你确定吗?" 他问

You realize you aren't sure at all. Can you solve this problem? Read this lesson, and by the end you'll be able to calculate the cosine of the difference of the angles.
::你意识到你根本不确定。你能解决这个问题吗? 读读这个课, 到最后你就能计算出角度差异的余弦。

Formulas for the Sum and Difference of Cosines
::共和和差异公式

When thinking about how to calculate values for trig functions, it is natural to consider what the value is for the trig function of a difference of two angles.
::当思考如何计算三角函数的值时,自然会考虑两个角度差异的三角函数的值。

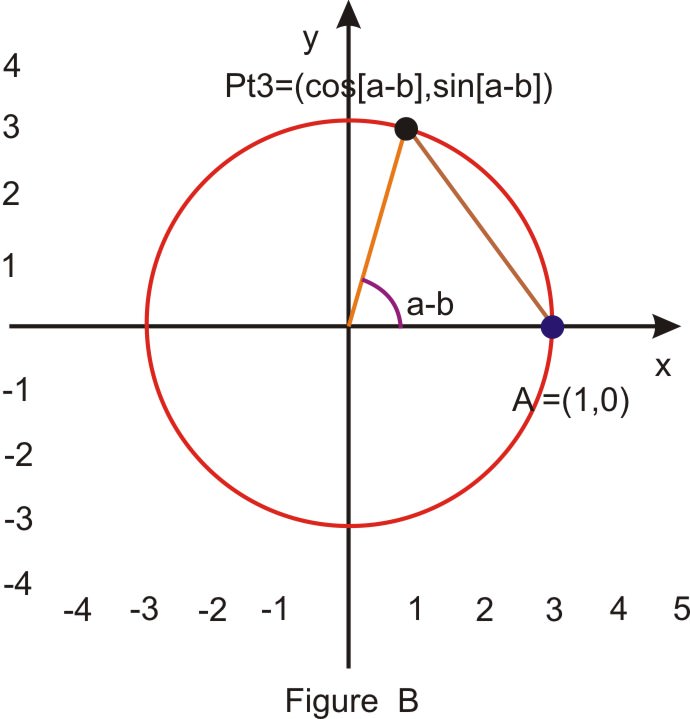
For example, is $\begin{align*}\cos 15^\circ = \cos (45^\circ - 30^\circ)\end{align*}$ ? Upon appearance, yes, it is. This section explores how to find an expression that would equal $\begin{align*}\cos (45^\circ - 30^\circ)\end{align*}$ . To simplify this, let the two given angles be $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ where $\begin{align*}0 < b < a < 2\pi\end{align*}$ .
::例如,是 cos15cos( 4530) 吗? ? 外观时, 是, 是。本节探讨如何找到一个表达式, 等于 cos( 4530) 。要简化这一点, 请让给定的两个角度在 0<b<a<2) 的 a 和 b 。

Begin with the unit circle and place the angles $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ in standard position as shown in Figure A. Point Pt1 lies on the terminal side of $\begin{align*}b\end{align*}$ , so its coordinates are $\begin{align*}(\cos b, \sin b)\end{align*}$ and Point Pt2 lies on the terminal side of $\begin{align*}a\end{align*}$ so its coordinates are $\begin{align*}(\cos a, \sin a)\end{align*}$ . Place the $\begin{align*}a - b\end{align*}$ in standard position, as shown in Figure B. The point A has coordinates $\begin{align*}(1, 0)\end{align*}$ and the Pt3 is on the terminal side of the angle $\begin{align*}a - b\end{align*}$ , so its coordinates are $\begin{align*}(\cos[a - b], \sin[a - b])\end{align*}$ .
::以单位圆开始,并将角a和角b置于标准位置,如图A所示。点Pt1位于b的终点面,其坐标为(cosb,sinb),点Pt2位于其坐标的终点面(cosa,sina)。将a-b置于标准位置,如图B所示。A点具有坐标(1,0),Pt3位于角度a-b的终点面,其坐标为(cos[a-b],sin{a-b]。

Triangles $\begin{align*}OP_1P_2\end{align*}$ in figure A and Triangle $\begin{align*}OAP_3\end{align*}$ in figure B are congruent. (Two sides and the included angle, $\begin{align*}a - b\end{align*}$ , are equal). Therefore the unknown side of each triangle must also be equal. That is: $\begin{align*}d\ (A, P_3) = d\ (P_1, P_2)\end{align*}$
::图A的三角形OP1P2和图B的三角形 OAP3是相同的。 (两边和包括的角度,a-b是相等的) 因此,每个三角形的未知边也必须相等。也就是说: d (A,P3)=d (P1,P2)

Applying the distance formula to the triangles in Figures A and B and setting them equal to each other:
::将距离公式应用到图A和图B中的三角形,并设定对等公式:

$\begin{aligned} \sqrt{[\cos (a - b) - 1]^{2} + [\sin (a - b) - 0]^{2}} = \sqrt{(\cos a - \cos b)^{2} + (\sin a - \sin b)^{2}} \end{aligned}$
$\begin{align*}\sqrt{[\cos (a-b)-1]^2 + [\sin (a-b)-0]^2} = \sqrt{(\cos a - \cos b)^2+(\sin a - \sin b)^2}\end{align*}$
::[cos(a-b)-1]2+[sin(a-b)-0]2=(cosa-cosb)2+(sina-sinb)2

Square both sides to eliminate the square root.
::双方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方

$\begin{aligned} [\cos (a - b) - 1]^{2} + [\sin (a - b) - 0]^{2} = (\cos a - \cos b)^{2} + (\sin a - \sin b)^{2} \end{aligned}$
$\begin{align*}[\cos (a - b) - 1]^2 + [\sin (a-b)-0]^2 = (\cos a - \cos b)^2 + (\sin a - \sin b)^2\end{align*}$
::[cos(a-b)-1]2+[sin(a-b)-0]2=(cosa-cosb)2+(sina-sinb)2

FOIL all four squared expressions and simplify.
::FOIL 所有四个方形表达式并简化。

$\begin{aligned} \cos^{2} (a - b) - 2 \cos (a - b) + 1 + \sin^{2} (a - b) & = \cos^{2} a - 2 \cos a \cos b + \cos^{2} b + \sin^{2} a - 2 \sin a \sin b + \sin^{2} b \\ \underset{⏟}{\sin^{2} (a - b) + \cos^{2} (a - b)} - 2 \cos (a - b) + 1 & = \underset{⏟}{\sin^{2} a + \cos^{2} a} - 2 \cos a \cos b + \underset{⏟}{\sin^{2} b + \cos^{2} b} - 2 \sin a \sin b \\ 1 - 2 \cos (a - b) + 1 & = 1 - 2 \cos a \cos b + 1 - 2 \sin a \sin b \\ 2 - 2 \cos (a - b) & = 2 - 2 \cos a \cos b - 2 \sin a \sin b \\ - 2 \cos (a - b) & = - 2 \cos a \cos b - 2 \sin a \sin b \\ \cos (a - b) & = \cos a \cos b + \sin a \sin b \end{aligned}$
$\begin{align*}\cos^2 (a-b)-2 \cos(a-b)+ 1 + \sin^2 (a-b) & = \cos^2 a - 2 \cos a \cos b + \cos^2 b + \sin^2 a - 2 \sin a \sin b + \sin^2 b \\ \underbrace{\sin^2 (a-b) + \cos^2 (a-b)} - 2 \cos (a-b) + 1 & = \underbrace{\sin^2 a + \cos^2 a} - 2 \cos a \cos b + \underbrace{\sin^2 b + \cos^2 b} - 2 \sin a \sin b \\ 1-2 \cos (a-b) + 1 & = 1 - 2 \cos a \cos b + 1 - 2 \sin a \sin b \\ 2-2 \cos (a-b) & = 2-2 \cos a \cos b -2 \sin a \sin b \\ -2 \cos (a-b) & = -2 \cos a \cos b - 2 \sin a \sin b \\ \cos (a-b) & = \cos a \cos b + \sin a \sin b\end{align*}$
::2(a-b) 22(a-) 2(a-b) 至22(a-b) 至22(a-b) 至 2(a-b) 至 2(a-b) 至 2(a-b) 至 22(a-b) 至 22(a-b) +1 至 22(a-b) +1 至 222(a-b) 22(a-b) 222(a-b+ 22(a-b) 1-1-1-2-22(b) 至222(b) (ab)

In $\begin{align*}\cos(a - b) = \cos a \cos b + \sin a \sin b\end{align*}$ , the difference formula for cosine, you can substitute $\begin{align*}a - (- b) = a + b\end{align*}$ to obtain: $\begin{align*}\cos(a + b) = \cos[a - (- b)]\end{align*}$ or $\begin{align*}\cos a \cos (- b) + \sin a \sin(-b)\end{align*}$ . since $\begin{align*}\cos(-b) = \cos b\end{align*}$ and $\begin{align*}\sin (-b) = -\sin b\end{align*}$ , then $\begin{align*}\cos(a + b) = \cos a \cos b - \sin a \sin b\end{align*}$ , which is the sum formula for cosine.
::在cos(a-b) =cosççacosb+sinsinb, cosine的差值公式中, 您可以替换 a- (b) =a+b, 获取: cos(a+b) =cos[a-(b)] 或cosçacos(b) +sinsin(b) 。因为cos(b) =cosíb 和 sin(b) 和 sin(b) 和 cos(a+b) =cosçacosb-sin asinb, 这是共和的共和公式。

Using the Cosine Difference Formula
::使用 Cosine 差异公式

1. Find an equivalent form of $\begin{align*}\cos \left (\frac{\pi}{2} - \theta \right )\end{align*}$ using the cosine difference formula .
::1. 使用余弦差差公式,寻找等效的cos(2)形式。

$\begin{aligned} \cos (\frac{π}{2} - θ) & = \cos \frac{π}{2} \cos θ + \sin \frac{π}{2} \sin θ \\ \cos (\frac{π}{2} - θ) & = 0 \times \cos θ + 1 \times \sin θ, substitute \cos \frac{π}{2} = 0 and \sin \frac{π}{2} = 1 \\ \cos (\frac{π}{2} - θ) & = \sin θ \end{aligned}$
$\begin{align*}\cos \left (\frac{\pi}{2} - \theta \right ) & = \cos \frac{\pi}{2} \cos \theta + \sin \frac{\pi}{2} \sin \theta \\ \cos \left (\frac{\pi}{2} - \theta \right ) & = 0 \times \cos \theta + 1 \times \sin \theta, \ \text{substitute}\ \cos \frac{\pi}{2} = 0 \ \text{and}\ \sin \frac{\pi}{2} = 1 \\ \cos \left (\frac{\pi}{2} - \theta \right ) & = \sin \theta\end{align*}$
::========================================================================================================================================================================================================================================================================================================================================================================================

We know that is a true identity because of our understanding of the curves, which are a phase shift of $\begin{align*}\frac{\pi}{2}\end{align*}$ off from each other.
::我们知道,这是真正的特征,因为我们理解曲线,曲线是两分之一的相去甚远。

The cosine formulas can also be used to find exact values of cosine that we weren’t able to find before, such as $\begin{align*}15^\circ =(45^\circ - 30^\circ), 75^\circ =(45^\circ + 30^\circ)\end{align*}$ , among others.
::comsine 配方也可以用来找到我们之前无法找到的 comsine 的准确值, 例如15(4530),75(4530)等。

2. Find the exact value of $\begin{align*}\cos 15^\circ\end{align*}$
::2. 查明Cos15的准确值

Use the difference formula where $\begin{align*}a = 45^\circ\end{align*}$ and $\begin{align*}b = 30^\circ\end{align*}$ .
::在 a=45 和 b=30 中使用差值公式。

$\begin{aligned} \cos (45^{\circ} - 30^{\circ}) & = \cos 45^{\circ} \cos 30^{\circ} + \sin 45^{\circ} \sin 30^{\circ} \\ \cos 15^{\circ} & = \frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \times \frac{1}{2} \\ \cos 15^{\circ} & = \frac{\sqrt{6} + \sqrt{2}}{4} \end{aligned}$
$\begin{align*}\cos (45^\circ - 30^\circ) & = \cos 45^\circ \cos 30^\circ + \sin 45^\circ \sin 30^\circ \\ \cos 15^\circ & = \frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \times \frac{1}{2} \\ \cos 15^\circ & = \frac{\sqrt{6} + \sqrt{2}}{4}\end{align*}$
::=========================================================================================================================================== ========================================================= ====================================================================================================================================================================================================================================================================== = = = = = = = = = = = = = = = = = = = = = = = =

3. Find the exact value of $\begin{align*}\cos \frac{5 \pi}{12}\end{align*}$ , in radians.
::3. 查找以弧度表示的COs512的准确值。

$\begin{align*}\cos \frac{5 \pi}{12} = \cos \left (\frac{\pi}{4} + \frac{\pi}{6} \right )\end{align*}$ , notice that $\begin{align*}\frac{\pi}{4} = \frac{3 \pi}{12}\end{align*}$ and $\begin{align*}\frac{\pi}{6} = \frac{2 \pi}{12}\end{align*}$
::512=cos(46),通知 4=312和6=212

$\begin{aligned} \cos (\frac{π}{4} + \frac{π}{6}) & = \cos \frac{π}{4} \cos \frac{π}{6} - \sin \frac{π}{4} \sin \frac{π}{6} \\ \cos \frac{π}{4} \cos \frac{π}{6} - \sin \frac{π}{4} \sin \frac{π}{6} & = \frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2} \times \frac{1}{2} \\ = \frac{\sqrt{6} - \sqrt{2}}{4} \end{aligned}$
$\begin{align*}\cos \left (\frac{\pi}{4} + \frac{\pi}{6} \right ) & = \cos \frac{\pi}{4} \cos \frac{\pi}{6} - \sin \frac{\pi}{4} \sin \frac{\pi}{6} \\ \cos \frac{\pi}{4} \cos \frac{\pi}{6} - \sin \frac{\pi}{4} \sin \frac{\pi}{6} & = \frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2} \times \frac{1}{2} \\ & = \frac{\sqrt{6} - \sqrt{2}}{4}\end{align*}$
:46) =cos446-sin}4466444446-sin}46=22×32_22×12=6～24

Examples
::实例

Example 1
::例1

Earlier, you were asked if you can calculate the cosine of the difference between the two angles.
::早些时候,有人问您能否计算出两个角度之间的差的余弦值。

It would seem that your friend was having some fun with you, since he figured you didn't know the cosine difference formula. But now, with this formula in hand, you can readily solve for the difference of the two angles:
::你的朋友似乎跟你玩得很开心,因为他觉得你不知道余弦不同配方。但是现在,有了这个配方,你就可以很容易地解决两个角度的差异:

$\begin{aligned} \cos (110^{\circ} - 80^{\circ}) \\ = (\cos 110^{\circ}) (\cos 80^{\circ}) + (\sin 110^{\circ}) (\sin 80^{\circ}) \\ = (- .342) (.174) + (.9397) (.9848) \\ = - .0595 + .9254 = .8659 \end{aligned}$
$\begin{align*} \cos(110^\circ - 80^\circ)\\ = (\cos 110^\circ)(\cos 80^\circ) + (\sin 110^\circ)(\sin 80^\circ)\\ = (-.342)(.174) + (.9397)(.9848)\\ = -.0595 + .9254 = .8659 \end{align*}$
:11080) =(cos 110 (cos80) +(sin 110)(sin80) =(- 342) (174) +(9397) (.9848) .0595+.9254=.8659)

Therefore,
::因此,

$\begin{align*}\cos (110^\circ - 80^\circ) = .8659\end{align*}$
:11080)=8659

Example 2
::例2

Find the exact value for $\begin{align*}\cos \frac{5 \pi}{12}\end{align*}$
::查找 cos512 的确切值

$\begin{aligned} \cos \frac{5 π}{12} & = \cos (\frac{2 π}{12} + \frac{3 π}{12}) = \cos (\frac{π}{6} + \frac{π}{4}) = \cos \frac{π}{6} \cos \frac{π}{4} - \sin \frac{π}{6} \sin \frac{π}{4} \\ = \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} - \frac{1}{2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{6}}{4} - \frac{\sqrt{2}}{4} = \frac{\sqrt{6} - \sqrt{2}}{4} \end{aligned}$
$\begin{align*}\cos \frac{5 \pi}{12} & = \cos \left (\frac{2 \pi}{12} + \frac{3 \pi}{12} \right ) = \cos \left (\frac{\pi}{6} + \frac{\pi}{4} \right ) = \cos \frac{\pi}{6} \cos \frac{\pi}{4} - \sin \frac{\pi}{6} \sin \frac{\pi}{4} \\ & = \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} - \frac{1}{2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{6}}{4} - \frac{\sqrt{2}}{4} = \frac{\sqrt{6} - \sqrt{2}}{4}\end{align*}$
::=cos =cos =cos =cos =cos =cos =cos =cos = 6cos =4 -sin = 6sin=4= 3222 - 12Q22=64 - 24=624

Example 3
::例3

Find the exact value for $\begin{align*}\cos \frac{7 \pi}{12}\end{align*}$
::查找 cos712 的确切值

$\begin{aligned} \cos \frac{7 π}{12} & = \cos (\frac{4 π}{12} + \frac{3 π}{12}) = \cos (\frac{π}{3} + \frac{π}{4}) = \cos \frac{π}{3} \cos \frac{π}{4} - \sin \frac{π}{3} \sin \frac{π}{4} \\ = \frac{1}{2} \cdot \frac{\sqrt{2}}{2} - \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{4} - \frac{\sqrt{6}}{4} = \frac{\sqrt{2} - \sqrt{6}}{4} \end{aligned}$
$\begin{align*}\cos \frac{7 \pi}{12} & = \cos \left (\frac{4 \pi}{12} + \frac{3 \pi}{12} \right ) = \cos \left (\frac{\pi}{3} + \frac{\pi}{4} \right ) = \cos \frac{\pi}{3} \cos \frac{\pi}{4} - \sin \frac{\pi}{3} \sin \frac{\pi}{4} \\ & = \frac{1}{2} \cdot \frac{\sqrt{2}}{2} - \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{4} - \frac{\sqrt{6}}{4} = \frac{\sqrt{2} - \sqrt{6}}{4}\end{align*}$
::712=cos(412+312)=cos(34)=cos334-sin34=1222-3222=24-64=264

Example 4
::例4

Find the exact value for $\begin{align*}\cos 345^\circ\end{align*}$
::查找 cos345 的准确值@ label

$\begin{aligned} \cos 345^{\circ} & = \cos (315^{\circ} + 30^{\circ}) = \cos 315^{\circ} \cos 30^{\circ} - \sin 315^{\circ} \sin 30^{\circ} \\ = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} - (- \frac{\sqrt{2}}{2}) \cdot \frac{1}{2} = \frac{\sqrt{6} + \sqrt{2}}{4} \end{aligned}$
$\begin{align*}\cos 345^\circ & = \cos(315^\circ + 30^\circ) = \cos 315^\circ \cos 30^\circ - \sin 315^\circ \sin 30^\circ \\ & = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} - (-\frac{\sqrt{2}}{2}) \cdot \frac{1}{2} = \frac{\sqrt{6} + \sqrt{2}}{4}\end{align*}$
::==6+24 =6+ =6+24 =6+24=6+

Review
::回顾

Find the exact value for each cosine expression.
::查找每个余弦表达式的确切值。

$\begin{align*}\cos75^\circ\end{align*}$
::COS75

$\begin{align*}\cos105^\circ\end{align*}$
::来来来来来来回回回回回回回回回回回回回

$\begin{align*}\cos165^\circ\end{align*}$
::1651151111111111111111111111111221222222222222222222222222111122211112212211121111211211122

$\begin{align*}\cos255^\circ\end{align*}$
::

$\begin{align*}\cos-15^\circ\end{align*}$
:cos-15)

Write each expression as the cosine of an angle.
::将每个表达式写成角度的余弦。

$\begin{align*}\cos96^\circ\cos20^\circ+\sin96^\circ\sin20^\circ\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不!

$\begin{align*}\cos4x\cos3x-\sin4x\sin3x\end{align*}$
::COS4xcos3x-sin4xsin3x

$\begin{align*}\cos37^\circ\cos12^\circ+\sin37^\circ\sin12^\circ\end{align*}$
::37cos12sin37sin12

$\begin{align*}\cos59^\circ\cos10^\circ-\sin59^\circ\sin10^\circ\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}那又怎样呢? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}那又怎样呢? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}那又怎样呢?

$\begin{align*}\cos5y\cos2y+\sin5y\sin2y\end{align*}$
::5ycos2y+sin5ysin2y

Prove that $\begin{align*}\cos(x-\frac{\pi}{4})=\frac{\sqrt{2}}{2}(\cos(x)+\sin(x))\end{align*}$
::证明 cos(x4) =22 (cos(x)+sin(x))

If %3D%5Csin(x)%5Csin"> $\begin{align*}\cos(x)\cos(y)=\sin(x)\sin(y)\end{align*}$ , then what does $\begin{align*}\cos(x+y)\end{align*}$ equal?
::如果cos(x)cos=sin(x)sin,那么cos(x+y)等于什么?

Prove that $\begin{align*}\cos(x-\frac{\pi}{2})=\sin(x)\end{align*}$
::证明 cos( x2) =sin( x)

Use the fact that $\begin{align*}\cos(\frac{\pi}{2}-x)=\sin(x)\end{align*}$ (shown in examples), to show that $\begin{align*}\sin(\frac{\pi}{2}-x)=\cos(x)\end{align*}$ .
::使用 cos( 2- x) =sin( x)( 示例中显示) 来显示 sin( 2- x) =cos( x) 。

Prove that "> $\begin{align*}\cos(x-y)+\cos(x+y)=2\cos(x)\cos(y)\end{align*}$ .
::证明 cos( x-y) +cos( x+y) = 2cos( x) cos 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

余弦和差异公式

Formulas for the Sum and Difference of Cosines ::共和和差异公式

Using the Cosine Difference Formula ::使用 Cosine 差异公式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Formulas for the Sum and Difference of Cosines
::共和和差异公式

Using the Cosine Difference Formula
::使用 Cosine 差异公式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)