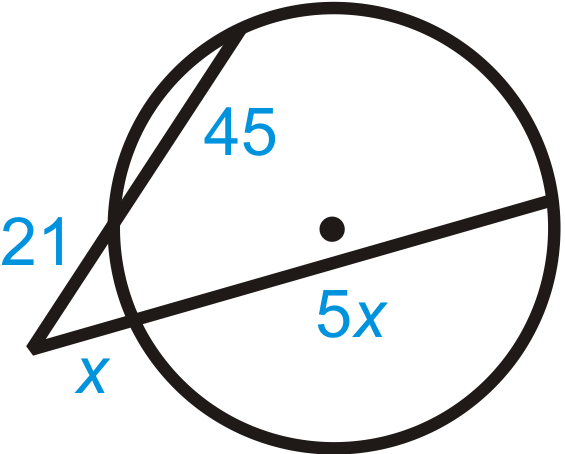9.10 封存物的片段

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 屏蔽区段的线段

  Collapse Expand

  屏蔽区段的线段

  播放段落

  Segments from Secants
  ::屏蔽区段的线段

  播放段落

  When two intersect outside a circle , the circle divides the secants into segments that are proportional with each other.
  ::当两个圆外交错时,该圆将分离者分成彼此相称的区段。

  播放段落

  Two Secants Segments Theorem : If two secants are drawn from a common point outside a circle and the segments are labeled as below, then $\begin{align*}a(a+b)=c(c+d)\end{align*}$ .
  ::两个分隔段的理论:如果从圆外的一个共同点抽出两个分离点,而各段的标签如下,则a(a+b)=c(c+d)。

  

  播放段落

  What if you were given a circle with two secants that intersect outside the circle? How could you use the length of some of the segments formed by their intersection to determine the lengths of the unknown segments?
  ::如果给您一个圆圈, 有两个空格在圆外交错, 如何使用它们交叉点形成的部分的长度来决定未知部分的长度 ?

  播放段落

  Examples
  ::实例

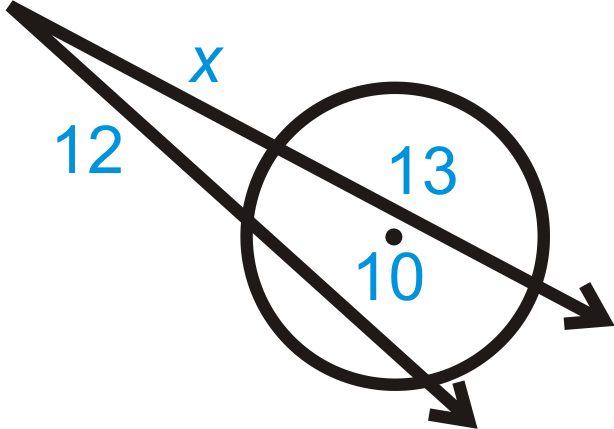
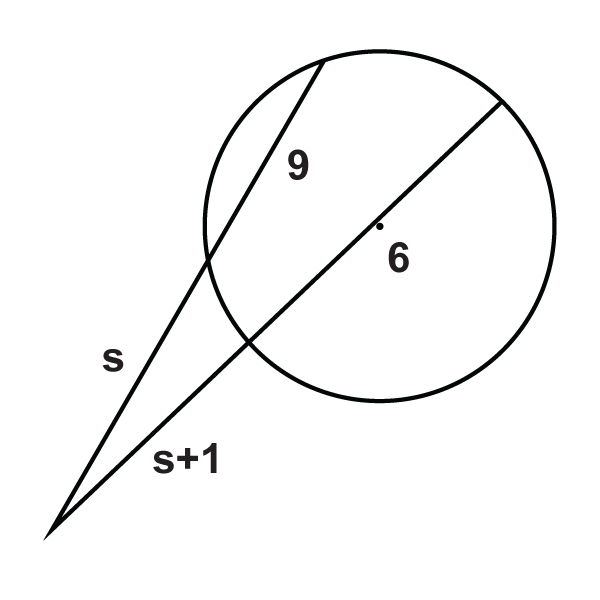
  播放段落

  Example 1
  ::例1

  播放段落

  Find $\begin{align*}x\end{align*}$ . Simplify any radicals.
  ::查找 x. 简化任何基数 。

  

  播放段落

  Use the Two Secants Segments Theorem.
  ::使用两个占位区段的定理。

  播放段落

  $$\begin{align*}8(8+x)&=6(6+18)\\64+8x&=144\\8x&=80\\x&=10\end{align*}$$
  ::8(8)+x)=6(6+18)64+8x=148x=80x=10

  播放段落

  Example 2
  ::例2

  播放段落

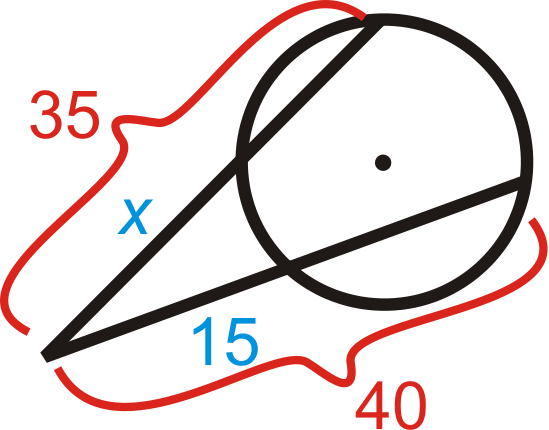
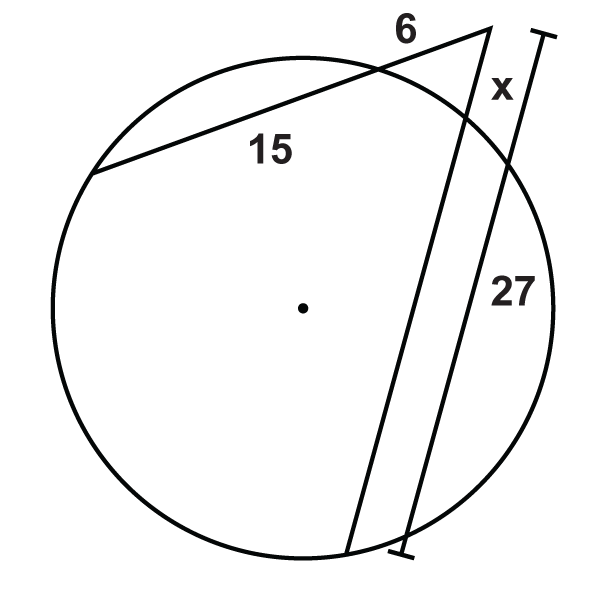
  Find  $\begin{align*}x\end{align*}$ . Simplify any radicals.
  ::查找 x. 简化任何基数 。

   

  播放段落

  Use the Two Secants Segments Theorem.
  ::使用两个占位区段的定理。

  播放段落

  $$\begin{align*}15(15+27)&=x\cdot 45\\630&=45x\\x&=14\end{align*}$$
  ::15(15+27)=x_455630=45xx=14

  播放段落

  Example 3
  ::例3

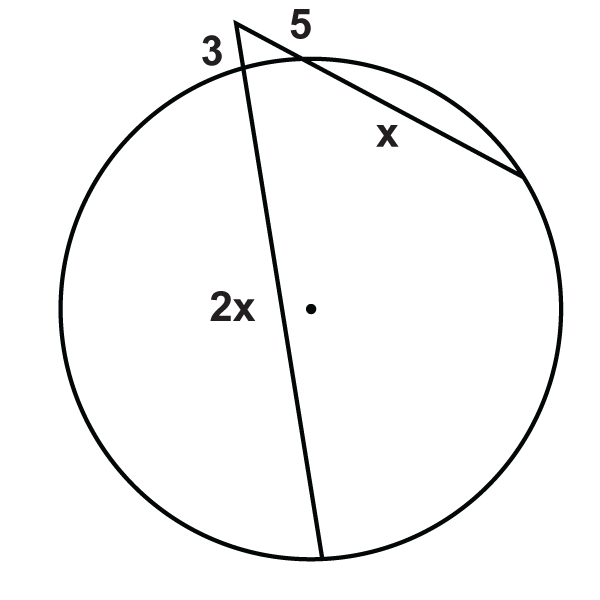
  播放段落

  Find the value of $\begin{align*}x\end{align*}$ .
  ::查找 x 的值。

  

  播放段落

  Use the Two Secants Segments Theorem.
  ::使用两个占位区段的定理。

  播放段落

  $$\begin{align*}18 \cdot (18+x) &= 16 \cdot (16+24)\\ 324+18x &= 256+384\\ 18x &= 316\\ x &= 17\frac{5}{9}\end{align*}$$
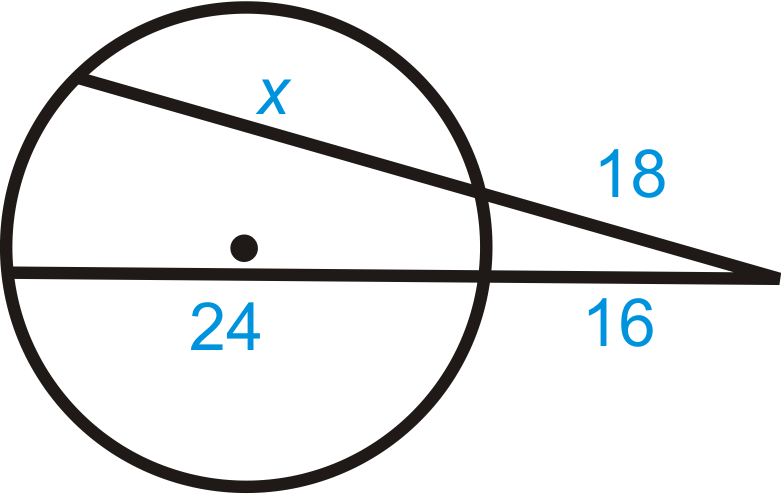
  ::18% (18+x) = 166% (16+24) 324+18x= 256+38418x= 316x= 1759

  播放段落

  Example 4
  ::例4

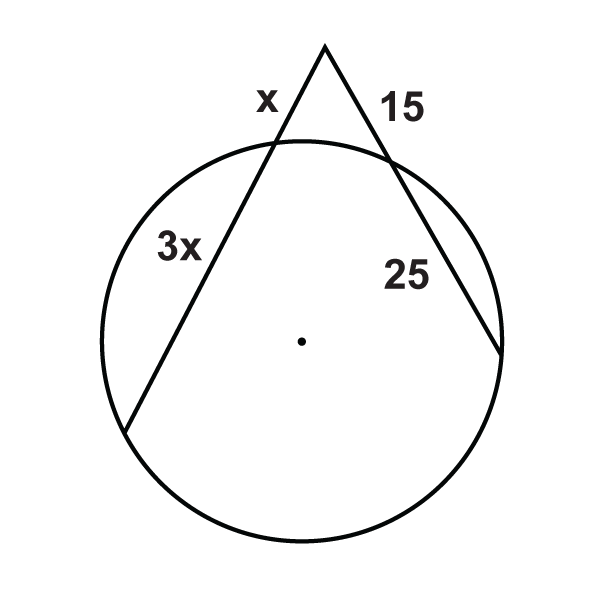
  播放段落

  Find the value of $\begin{align*}x\end{align*}$ .
  ::查找 x 的值。

  

  播放段落

  Use the Two Secants Segments Theorem.
  ::使用两个占位区段的定理。

  播放段落

  $$\begin{align*}x \cdot (x+x) &= 9 \cdot 32\\ 2x^2 &= 288\\ x^2 &= 144\\ x &=12, \ x\ne -12 \ (\text{length is not negative})\end{align*}$$
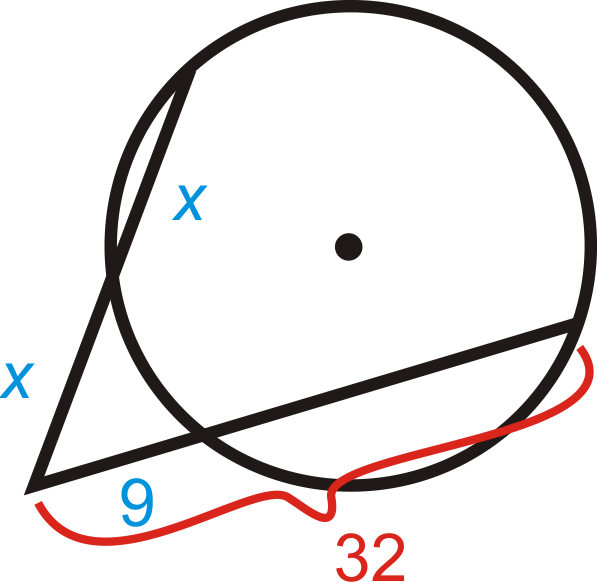
  ::x% (x+x) = 9 322x2= 288x2= 144x= 12, x12( 长度不为负)

  播放段落

  Example 5
  ::例5

  播放段落

  True or False: Two secants will always intersect outside of a circle.
  ::真理或假的:两个分离者总是在圆外交叉。

  播放段落

  False. If the two secants are parallel , they will never intersect. It's also possible for two secants to intersect inside a circle.
  ::假的。 如果两个分离区是平行的, 它们永远不会交叉。 两个分离区也可以在圆内交叉。

  播放段落

  Review
  ::回顾

  播放段落

  Fill in the blanks for each problem below. Then, solve for the missing segment.
  ::填满下面每个问题的空白。 然后解决缺失的部分 。

  1. 

  $\begin{align*}3(\underline{\;\;\;\;\;\;\;}+\underline{\;\;\;\;\;\;\;})=2(2+7)\end{align*}$

  2. 

  播放段落

  $\begin{align*}x \cdot \underline{\;\;\;\;\;\;\;}=8(\underline{\;\;\;\;\;\;\;}+\underline{\;\;\;\;\;\;\;})\end{align*}$
  ::x8

  播放段落

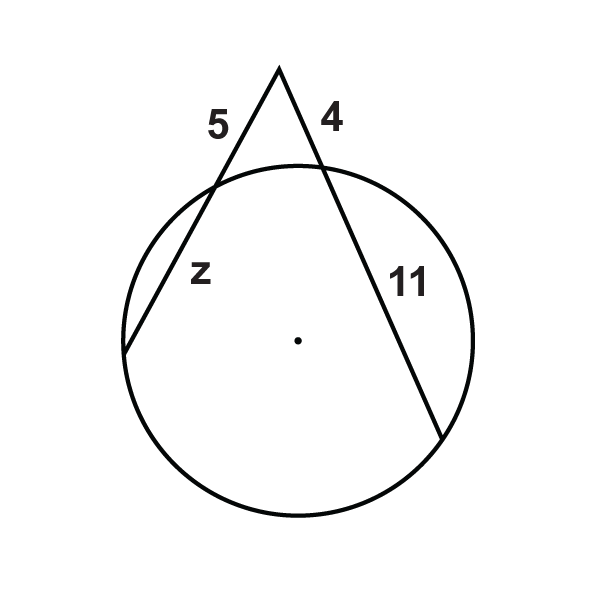
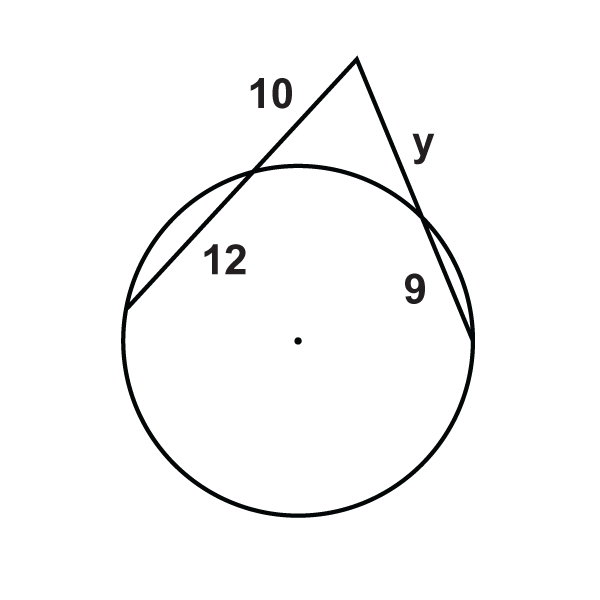
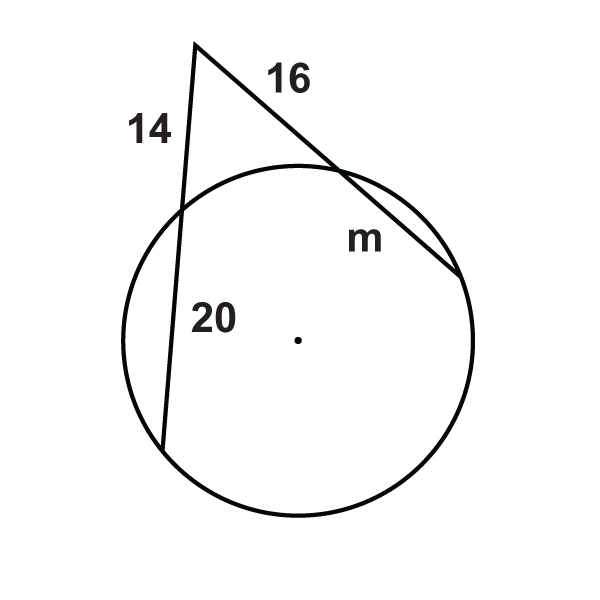
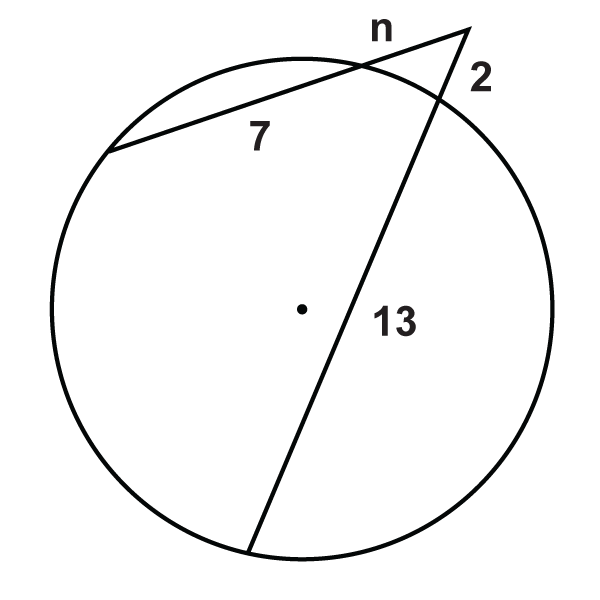
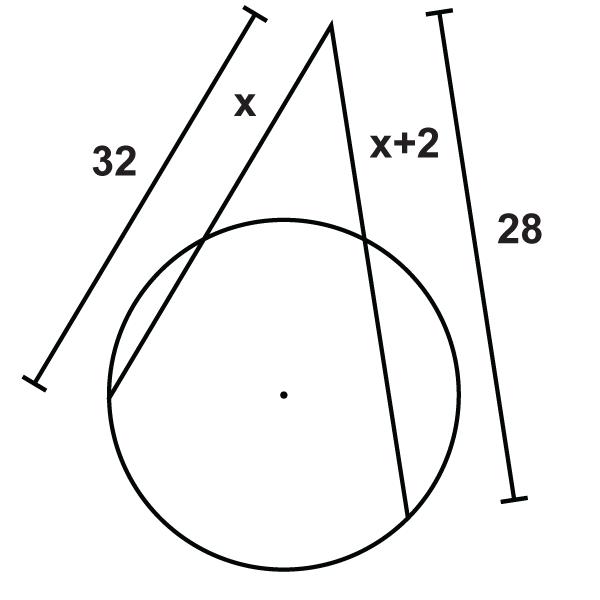
  Find $\begin{align*}x\end{align*}$ in each diagram below. Simplify any radicals and round your answers to the nearest hundredths place if needed.
  ::在下面的每个图表中查找 x。 如果需要, 简化任何基数, 并围绕您对最接近的百位的答案 。

  3. 
  4. 
  5. 

  播放段落
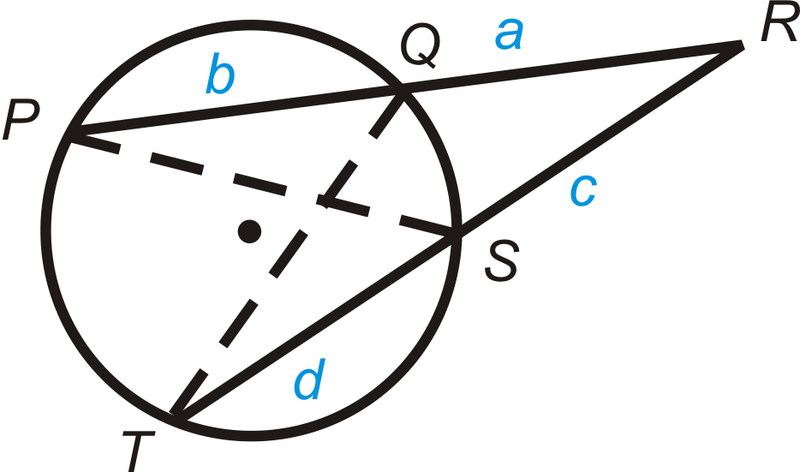
  6. Fill in the blanks of the proof of the Two Secants Segments Theorem.
     ::填满两个占位区段理论的空白

  播放段落

  Given : Secants $\begin{align*}\overline{PR}\end{align*}$ and $\begin{align*}\overline{RT}\end{align*}$
  ::特写:Secants PR和RT

  播放段落

  Prove : $\begin{align*}a(a+b)=c(c+d)\end{align*}$
  ::证明: a(a+b)=c(c+d)

  Statement	Reason
  1. Secants $\begin{align*}\overline{PR}\end{align*}$ and $\begin{align*}\overline{RT}\end{align*}$ with segments $\begin{align*}a, \ b, \ c,\end{align*}$ and $\begin{align*}d\end{align*}$ .	1. Given
  2. $\begin{align*}\angle R \cong \angle R\end{align*}$	2. Reflexive PoC
  3. $\begin{align*}\angle QPS \cong \angle STQ\end{align*}$	3. Congruent Inscribed Angles Theorem
  4. $\begin{align*}\triangle RPS \sim \triangle RTQ\end{align*}$	4. AA Similarity Postulate
  5. $\begin{align*}\frac{a}{c+d}=\frac{c}{a+b}\end{align*}$	5. Corresponding parts of similar triangles are proportional
  6. $\begin{align*}a(a+b)=c(c+d)\end{align*}$	6. Cross multiplication

  播放段落

  Solve for the unknown variable. Round your answers to the nearest hundredths place if needed.
  ::解决未知变量。 如果需要, 将您的答案转至最近的百个位置 。

  7. 
  8. 
  9. 
  10. 
  11. 
  12. 
  13. 
  14. 
  15. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。