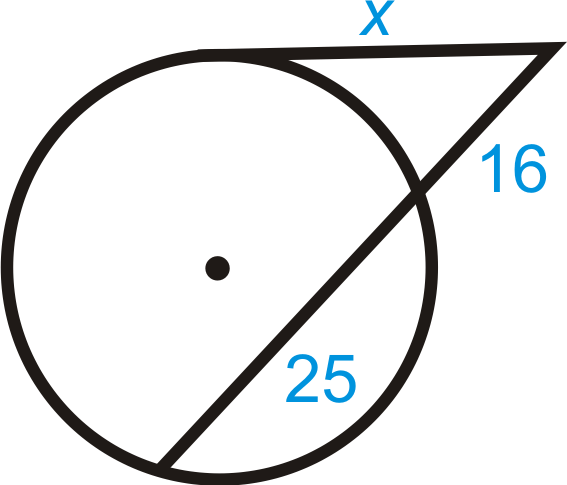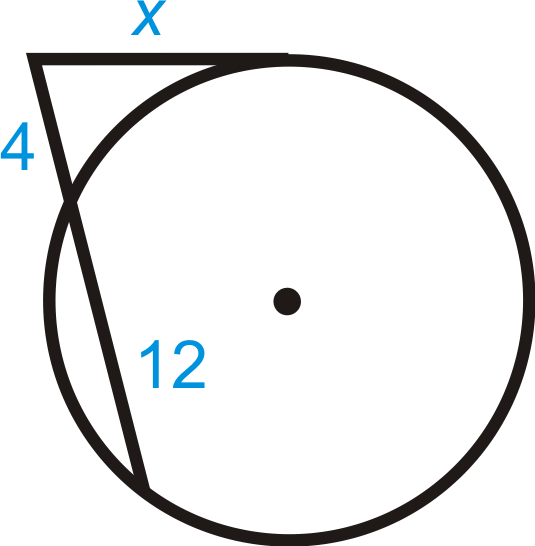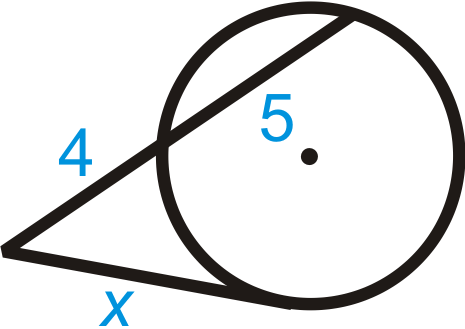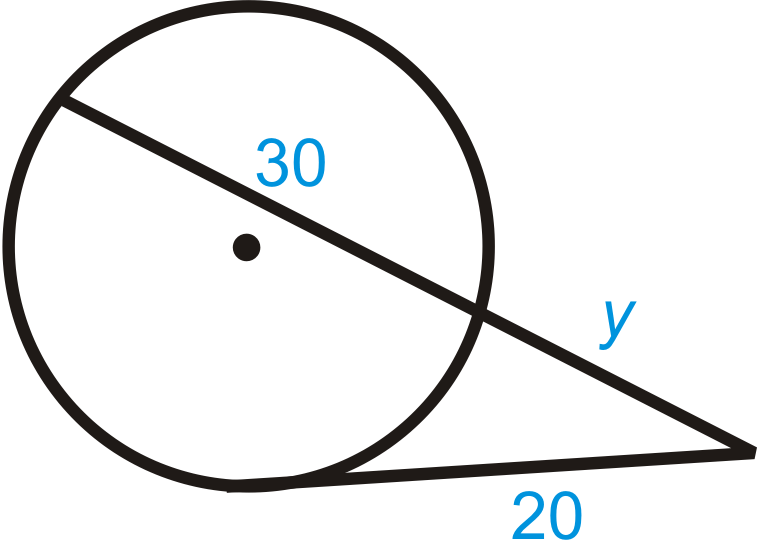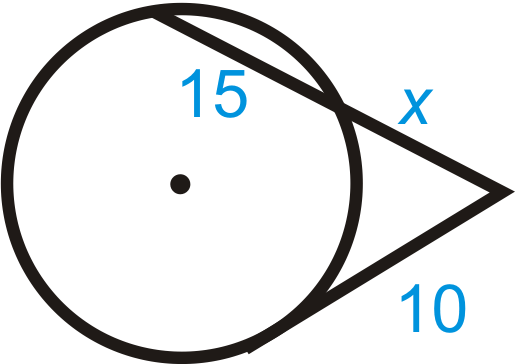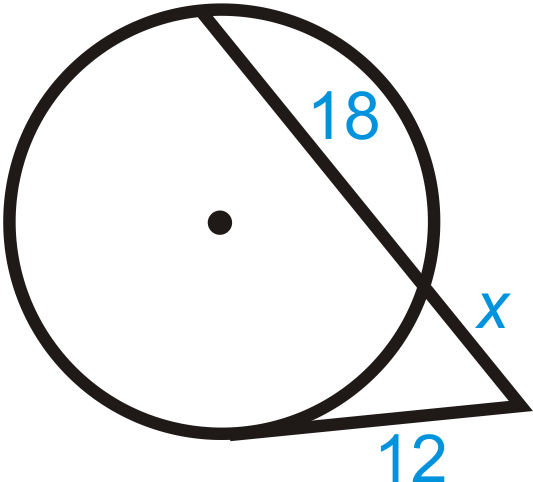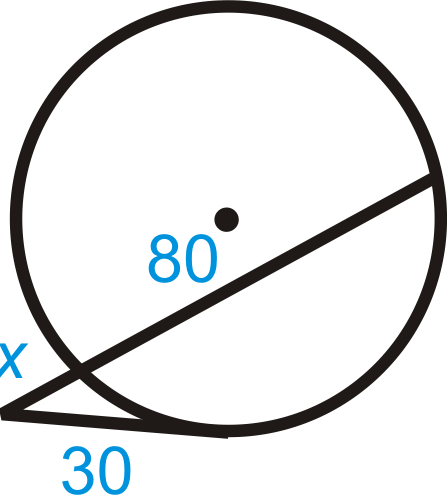9.11 封存物和切入物的片段

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 定点和定点的线段

  Collapse Expand

  定点和定点的线段

  播放段落

  Segments from Secants and Tangents
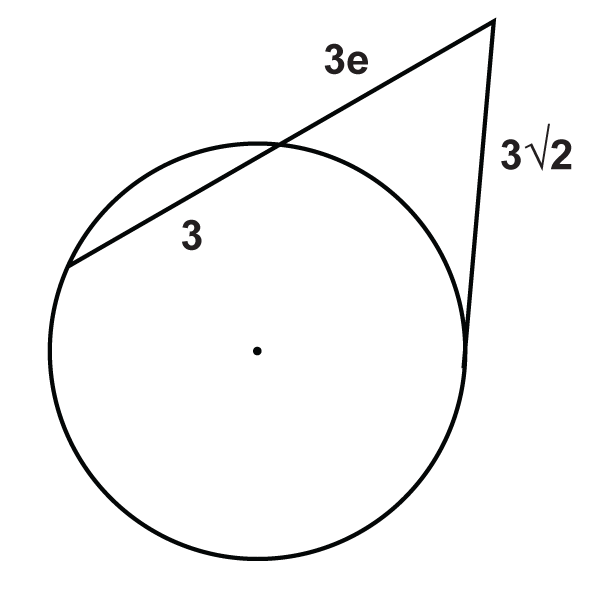
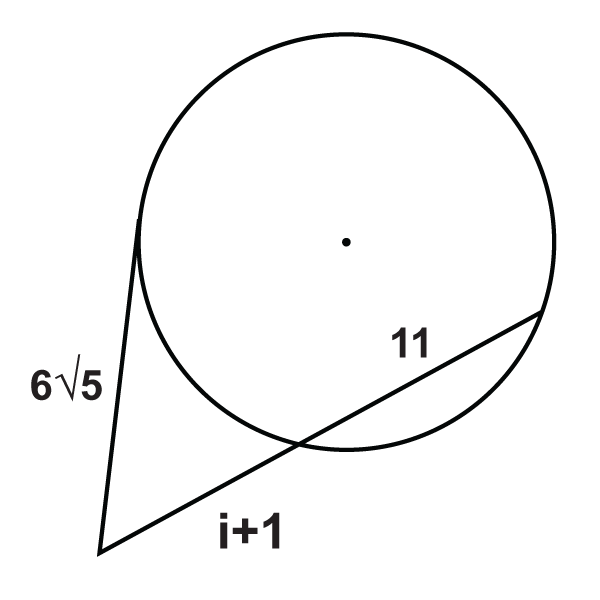
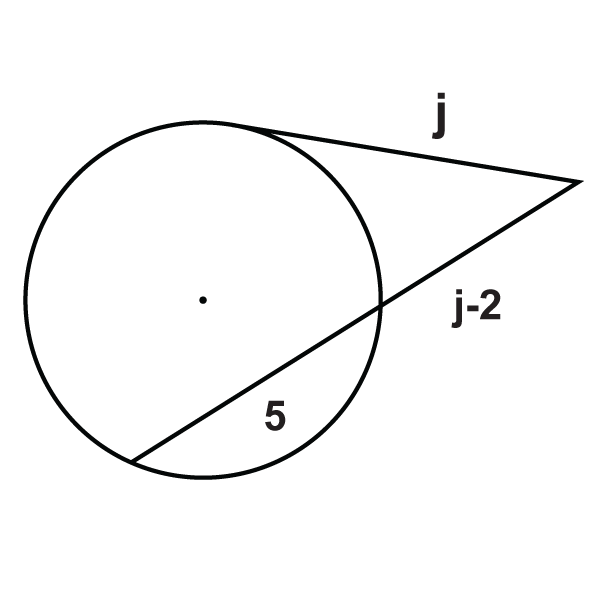
  ::定点和定点的线段

  播放段落

  If a tangent and secant meet at a common point outside a circle , the segments created have a similar relationship to that of two secant rays.
  ::如果偏差和偏差在一个圆圈外的共同点相会,所设立的区段与两个分离线具有类似关系。

  播放段落

  Tangent Secant Segment Theorem : If a tangent and a secant are drawn from a common point outside the circle (and the segments are labeled like the picture below), then $\begin{align*}a^2=b(b+c)\end{align*}$ .
  ::Tang Secant 段定理 : 如果从圆外的一个共同点抽出正切线和分离线(各段的标签与下图相类似), 那么 a2=b(b+c) 。

  

  播放段落

  What if you were given a circle with a tangent and a secant that intersect outside the circle? How could you use the length of some of the segments formed by their intersection to determine the lengths of the unknown segments?
  ::如果给您一个圆形,有正切和断层,在圆外交错,又如何呢?您如何使用通过交叉点形成的部分的长度来决定未知部分的长度?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Find $\begin{align*}x\end{align*}$ . Simplify any radicals.
  ::查找 x. 简化任何基数 。

  

  播放段落

  Use the Tangent Secant Segment Theorem.
  ::使用唐氏断层线段定理 。

  播放段落

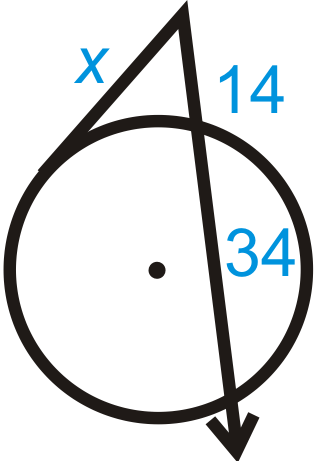
  $$\begin{align*} 18^2&=10(10+x)\\324&=100+10x\\224&=10x\\x&=22.4\end{align*}$$
  ::182=10(10+x)324=100+10x224=10xx=22.4

  播放段落

  Example 2
  ::例2

  播放段落

  Find  $\begin{align*}x\end{align*}$ . Simplify any radicals.
  ::查找 x. 简化任何基数 。

  

  播放段落

  Use the Tangent Secant Segment Theorem.
  ::使用唐氏断层线段定理 。

  播放段落

  $$\begin{align*}x^2&=16(16+25)\\x^2&=656\\x&=4\sqrt{41}\end{align*}$$
  ::x2=16( 16+25) x2=656x=441

  播放段落

  Example 3
  ::例3

  播放段落

  Find the length of the missing segment.
  ::查找缺失段的长度 。

  

  播放段落

  Use the Tangent Secant Segment Theorem.
  ::使用唐氏断层线段定理 。

  播放段落

  $$\begin{align*}x^2 &= 4(4+12)\\ x^2 &= 4 \cdot 16 = 64\\ x &= 8\end{align*}$$
  ::x2=4( 4+12) x2=416=64x=8

  播放段落

  Example 4
  ::例4

  播放段落

  Fill in the blank and then solve for the missing segment.
  ::填入空白,然后解答缺失的段段 。

  

  $\begin{align*}\underline{\;\;\;\;\;\;\;}=\underline{\;\;\;\;\;\;\;}(4+5)\end{align*}$

  播放段落

  $$\begin{align*}x^2&=4(4+5)\\x^2&=36\\x&=6\end{align*}$$
  ::x2=4( 4+5) x2=36x=6

  播放段落

  Example 5
  ::例5

  播放段落

  Find the value of the missing segment.
  ::查找缺失段的值 。

  

  播放段落

  Use the Tangent Secant Segment Theorem.
  ::使用唐氏断层线段定理 。

  播放段落

  $$\begin{align*}20^2 &= y(y+30)\\ 400 &= y^2+30y\\ 0 &= y^2+30y-400\!\\ 0 &= (y+40)(y-10)\!\\ y &= \xcancel{-40},10\end{align*}$$
  ::202=y(y+3040)400=y2+30y0=y2+30y-400=(y+40)(y-10y_40)40,10

  播放段落

  Review
  ::回顾

  播放段落

  Fill in the blanks for each problem below and then solve for the missing segment.
  ::填写下面每个问题的空白,然后解决缺失的部分。

  1. 

  播放段落

  $\begin{align*}10^2=x(\underline{\;\;\;\;\;\;\;}+\underline{\;\;\;\;\;\;\;})\end{align*}$
  ::102=x()

  播放段落

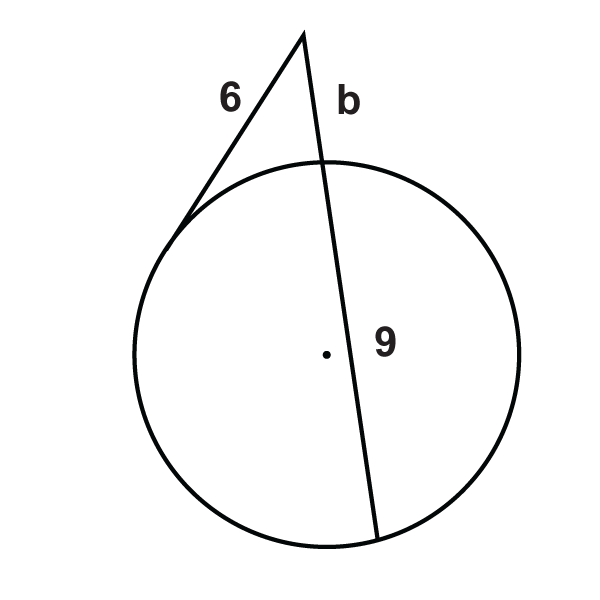
  Find $\begin{align*}x\end{align*}$ in each diagram below. Simplify any radicals.
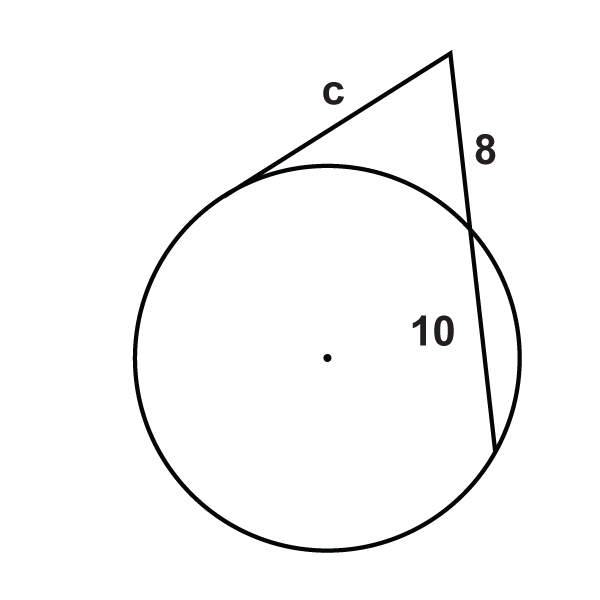
  ::在下图中查找 x。 简化任何基数 。

  2. 
  3. 
  4. 
  播放段落
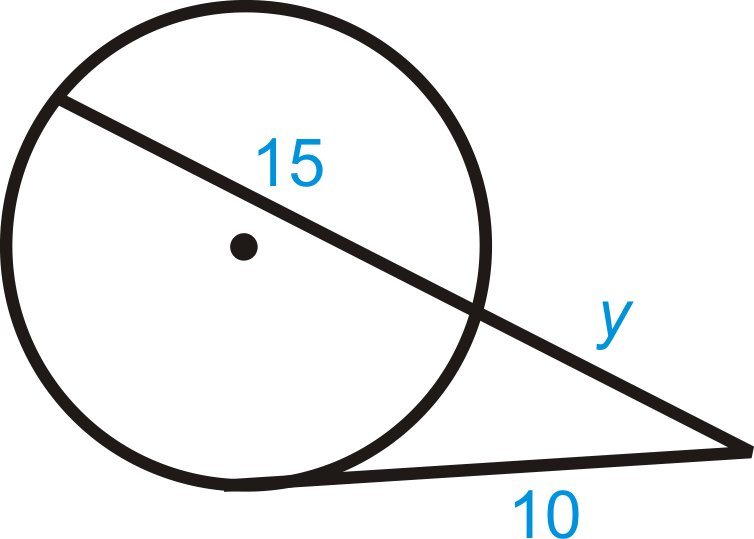
  5. Describe and correct the error in finding $\begin{align*}y\end{align*}$ . $$\begin{align*}10 \cdot 10&=y\cdot 15y\\ 100&=15y^2\\ \frac{20}{3}&=y^2\\ \frac{2\sqrt{15}}{3}&=y \quad {\color{red}\longleftarrow \ y} \ {\color{red}\text{is \underline{not} correct}}\end{align*}$$
     ::描述并更正查找 y. 10\ 10=y15y100=15y2203=y22153=yy y是\ underline{ not} 错误的描述并更正错误

  播放段落

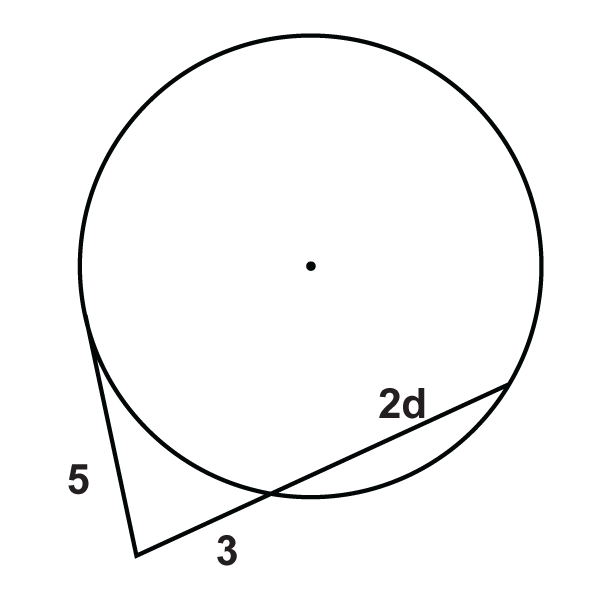
  Solve for the unknown variable. Round your answer to the nearest tenths place.
  ::解决未知变量。 将您的答案转至最近的十分位 。

  6. 
  7. 
  8. 
  9. 
  10. 
  11. 
  12. 
  13. 
  14. 
  15. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。