9.12 坐标平板中的圆圈

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 坐标平面中的圆圈

  Collapse Expand

  坐标平面中的圆圈

  播放段落

  Circles in the Coordinate Plane
  ::坐标平面中的圆圈

  播放段落

  Recall that a circle is the set of all points in a plane that are the same distance from the center . This definition can be used to find an equation of a circle in the coordinate plane.
  ::回顾一个圆是一个平面中所有点的集合, 与中点的距离相同。 此定义可用于在坐标平面中找到圆的方程式 。

  

  播放段落

  Let’s start with the circle centered at (0, 0). If $\begin{array}{r}(x,y)\end{array}$ is a point on the circle, then the distance from the center to this point would be the radius , $\begin{array}{r}r\end{array}$ . $\begin{array}{r}x\end{array}$ is the horizontal distance and $\begin{array}{r}y\end{array}$ is the vertical distance. This forms a right triangle . From the Pythagorean Theorem , the equation of a circle centered at the origin is $\begin{array}{r}{x}^2+y^2=r^2\end{array}$ .
  ::让我们从圆的中心点( 0, 0) 开始, 如果( x,y) 是圆的一个点, 那么从中间到这个点的距离将是半径, r. x 是水平距离, y 是垂直距离。 这形成一个右三角。 从 Pytagoren 理论, 圆的中心方程式是 x2+y2=r2 。

  播放段落

  The center does not always have to be on (0, 0). If it is not, then we label the center $\begin{array}{r}(h,k)\end{array}$ . We would then use the Distance Formula to find the length of the radius.
  ::中心不一定总是在( 0, 0) 上。 如果不是的话, 我们给中心贴上标签( h, k) 。 然后我们用距离公式来找到半径的长度 。

  播放段落

  

  $$\begin{array}{r}r=\sqrt{(x-h{)}^2+(y-k{)}^2}\end{array}$$

  
  ::r=(x-h)2+(y-k)2

  播放段落

  If you square both sides of this equation, then you would have the standard equation of a circle. The standard equation of a circle with center $\begin{array}{r}(h,k)\end{array}$ and radius $\begin{array}{r}r\end{array}$ is $\begin{array}{r}{r}^2=(x-h{)}^2+(y-k{)}^2\end{array}$ .
  ::如果您在此方程的两侧平方, 则您将拥有圆的标准方程。 圆的中心( h, k) 和半径 r 的标准方程是 r2=( x- h) 2+(y- k) 2。

  播放段落

  What if you were given the length of the radius of a circle and the coordinates of its center? How could you write the equation of the circle in the coordinate plane?
  ::如果给您给出圆半径的长度及其中心坐标, 您如何在坐标平面中写出圆的方程 ?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Find the center and radius of the following circle.
  ::查找以下圆的中间和半径。

  播放段落

  $\begin{array}{r}(x+2{)}^2+(y-5{)}^2=49\end{array}$
  :x+2)2+(y-5)2=49

  播放段落

  Rewrite the equation as $\begin{array}{r}(x-(-2){)}^2+(y-5{)}^2=7^2\end{array}$ . The center is (-2, 5) and $\begin{array}{r}r=7\end{array}$ .
  ::将方程重写为 (x- (-2)) 2+(y-5) 2=72。中心是 (-2) 5 和 r= 7。

  播放段落

  Keep in mind that, due to the minus signs in the formula, the coordinates of the center have the opposite signs of what they may initially appear to be.
  ::记住,由于公式中的减号,中心的坐标与最初看起来的相形见绌。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the center and radius of the following circle.
  ::查找以下圆的中间和半径。

  播放段落

  Find the equation of the circle with center (4, -1) and which passes through (-1, 2).
  ::查找圆形的方程式,以中间( 4, - 1) 和中间( 1, 2) 通过中间( 1, 2) 。

  播放段落

  First plug in the center to the standard equation.
  ::标准方程式中心的第一个插头

  播放段落

  $$\begin{array}{rl}(x-4{)}^2+(y-(-1){)}^2& =r^2\\ (x-4{)}^2+(y+1{)}^2& =r^2\end{array}$$

  
  :x-4)2+(y-(-1))2=r2(x-4)2+(y+1)2=r2

  播放段落

  Now, plug in (-1, 2) for $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ and solve for $\begin{array}{r}r\end{array}$ .
  ::现在, x 和 y 的插件 (-1, 2) 插入, r 的解答 。

  播放段落

  $$\begin{array}{rl}(-1-4{)}^2+(2+1{)}^2& =r^2\\ (-5{)}^2+(3{)}^2& =r^2\\ 25+9& =r^2\\ 34& =r^2\end{array}$$

  
  :-1-4)2+(2+1)2=r2(-5)2+(3)2=r225+9=r234=r2

  播放段落

  Substituting in 34 for $\begin{array}{r}{r}^2\end{array}$ , the equation is $\begin{array}{r}(x-4{)}^2+(y+1{)}^2=34\end{array}$ .
  ::方程(x-4)2+(y+1)2=34。

  播放段落

  Example 3
  ::例3

  播放段落

  Graph $\begin{array}{r}{x}^2+y^2=9\end{array}$ .
  ::图x2+y2=9。

  播放段落

  The center is (0, 0). Its radius is the square root of 9, or 3. Plot the center, plot the points that are 3 units to the right, left, up, and down from the center and then connect these four points to form a circle.
  ::中心为 0,0 半径为 9 或 3. 平方根 。 绘制中心, 绘制向右、 左、 上、 从中向下 3 个单位的点, 然后将这4 个点连接到圆形 。

  

  播放段落

  Example 4
  ::例4

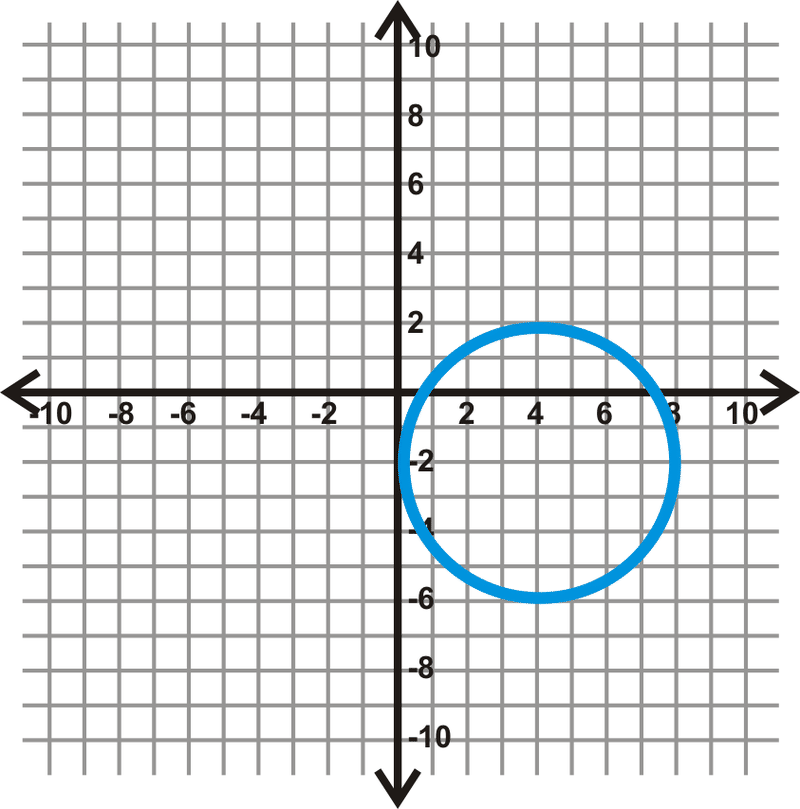
  播放段落

  Find the equation of the circle below.
  ::查找下方圆的方程式。

  

  播放段落

  First locate the center. Draw in the horizontal and vertical diameters to see where they intersect. 
  ::首先定位中心。 绘制水平和垂直直径以查看它们相交的位置 。

  

  播放段落

  From this, we see that the center is (-3, 3). If we count the units from the center to the circle on either of these diameters, we find $\begin{array}{r}r=6\end{array}$ . Plugging this into the equation of a circle, we get: $\begin{array}{r}(x-(-3){)}^2+(y-3{)}^2=6^2\end{array}$ or $\begin{array}{r}(x+3{)}^2+(y-3{)}^2=36\end{array}$ .
  ::我们从中可以看到中心是 (3,3,3) 。如果我们从中间点数到这些直径的圆形,我们就会发现 r=6. 将它插进圆形的方程中,我们就会得到x-(3))2+(y-3)2+(y-3)2=62或(x+3)2+(y-3)2=36。

  播放段落

  Example 5
  ::例5

  播放段落

  Determine if the following points are on $\begin{array}{r}(x+1{)}^2+(y-5{)}^2=50\end{array}$ .
  ::确定以下各点是否在(x+1)2+(y-5)2=50上。

  播放段落

  Plug in the points for $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ in $\begin{array}{r}(x+1{)}^2+(y-5{)}^2=50\end{array}$ .
  ::插入点xandyin(x+1)2+(y-5)2=50。

  1. (8, -3)
     
     $$\begin{array}{rl}(8+1{)}^2+(-3-5{)}^2& =50\\ 9^2+(-8{)}^2& =50\\ 81+64& \ne 50\end{array}$$

  播放段落

   (8, -3) is not on the circle
  :8, 3) 在圆上

  2. (-2, -2)
     
     $$\begin{array}{rl}(-2+1{)}^2+(-2-5{)}^2& =50\\ (-1{)}^2+(-7{)}^2& =50\\ 1+49& =50\end{array}$$

  播放段落

   (-2, -2) is on the circle
  :-2, 2) 在圆圈上

  播放段落

  Review
  ::回顾

  播放段落

  Find the center and radius of each circle. Then, graph each circle.
  ::查找每个圆的中间和半径。然后,绘制每个圆的图。

  播放段落
  1. $\begin{array}{r}(x+5{)}^2+(y-3{)}^2=16\end{array}$
     :x+5)2+(y-3)2=16
  播放段落
  2. $\begin{array}{r}{x}^2+(y+8{)}^2=4\end{array}$
     ::x2+(y+8)2=4
  播放段落
  3. $\begin{array}{r}(x-7{)}^2+(y-10{)}^2=20\end{array}$
     :-7)2+(y-10)2=20
  播放段落
  4. $\begin{array}{r}(x+2{)}^2+y^2=8\end{array}$
     :x+2)2+y2=8

  播放段落

  Find the equation of the circles below.
  ::找到下面圆圈的方程

  5. 
  6. 
  7. 
  8. 
  播放段落
  9. Is (-7, 3) on $\begin{array}{r}(x+1{)}^2+(y-6{)}^2=45\end{array}$ ?
     :7,3)在(x+1)2+(y-6)2=45上吗?
  播放段落
  10. Is (9, -1) on $\begin{array}{r}(x-2{)}^2+(y-2{)}^2=60\end{array}$ ?
      :9,-1)在(x-2)2+(y-2)2=60上吗?
  播放段落
  11. Is (-4, -3) on $\begin{array}{r}(x+3{)}^2+(y-3{)}^2=37\end{array}$ ?
      :4)-3在(x+3)2+(y-3)2=37上吗?
  播放段落
  12. Is (5, -3) on $\begin{array}{r}(x+1{)}^2+(y-6{)}^2=45\end{array}$ ?
      :5,3)在(x+1)2+(y-6)2=45上吗?

  播放段落

  Find the equation of the circle with the given center and point on the circle.
  ::查找圆的方程式,在圆上找到给定的中心点。

  播放段落
  13. center: (2, 3), point: (-4, -1)
      ::中心2,3),点4,4,1)
  播放段落
  14. center: (10, 0), point: (5, 2)
      ::中枢: (10,0) 点: (5,2)
  播放段落
  15. center: (-3, 8), point: (7, -2)
      ::中心3,8),点7,2)
  播放段落
  16. center: (6, -6), point: (-9, 4)
      ::中中6,6,-6),点9,4)

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。