10.6 伦布斯和克特的面积和周边

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 伦布斯和克特的面积和周边

  Collapse Expand

  伦布斯和克特的面积和周边

  播放段落

  Area and Perimeter of Rhombuses and Kites
  ::伦布斯和克特的面积和周边

  播放段落

  Recall that a rhombus is a quadrilateral with four congruent sides and a is a quadrilateral with distinct adjacent congruent sides. Both of these quadrilaterals have perpendicular diagonals , which is how we are going to find their areas.
  ::回顾暴风雨是四面形的四边形,四面形是四面形的四边形,另一面形的四边形与相邻的四边形不同。 这两个四边形都有直角形的三角形,这就是我们如何找到它们的区域。

  

  播放段落

  Notice that the diagonals divide each quadrilateral into 4 triangles. If we move the two triangles on the bottom of each quadrilateral so that they match up with the triangles above the horizontal diagonal , we would have two .
  ::注意对角线将每个四边形分隔为 4 个三角形。 如果我们将每个四边形底部的两个三角形移动, 以便它们与水平对角上方的三角形匹配, 我们就会有两个三角形 。

  

  播放段落

  So, the height of these rectangles is half of one of the diagonals and the base is the length of the other diagonal.
  ::因此,这些矩形的高度是对角体的半数, 基数是另一对角体的长度。

  播放段落

  The area of a rhombus or a kite is $\begin{align*}A=\frac{1}{2} d_1 d_2\end{align*}$
  ::暴风车或风筝区域为A=12d1d2

  播放段落

  What if you were given a kite or a rhombus and the size of its two diagonals? How could you find the total distance around the kite or rhombus and the amount of space it takes up? 
  ::如果给了你风筝或红灯,它的两个对角的大小又有多大呢?你怎么能找到风筝或红灯周围的距离,以及它所占用的空间的大小?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

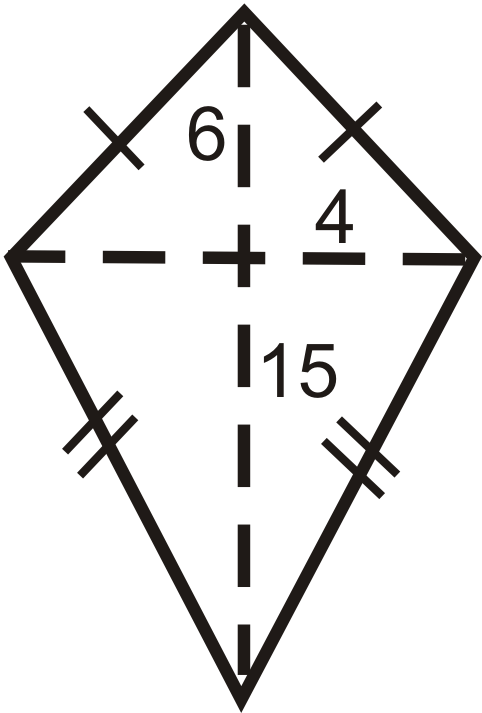
  播放段落

  Find the perimeter and area of the kite below.
  ::找出风筝下面的周界和地区

  

  播放段落

  In a kite, there are two pairs of . Use the Pythagorean Theorem to find the lengths of sides or diagonals.
  ::在风筝里,有两对,用毕达哥伦神话 来寻找侧面或对角的长度。

  播放段落

  $$\begin{align*}&\text{Smaller diagonal portion} && \text{Larger diagonal portion}\\ 20^2+d_s^2&=25^2 && 20^2+d_l^2=35^2\\ d_s^2&=225 && \qquad \ \ d_l^2=825\\ d_s&=15 \ units && \qquad \quad d_l=5\sqrt{33} \ units\end{align*}$$
  ::弧二角部分 202+d2s=252202+d2l=352d2s=225 d2l=825ds=15 单位dl=533 单位

  播放段落

  $$\begin{align*}A=\frac{1}{2} \left(15+5 \sqrt{33} \right)(40) \approx 874.5 \ units^2 && P=2(25)+2(35)=120 \ units\end{align*}$$
  ::A=12(15+533)(40)874.5单位2P=2(25)+2(35)=120单位

  播放段落

  Example 2
  ::例2

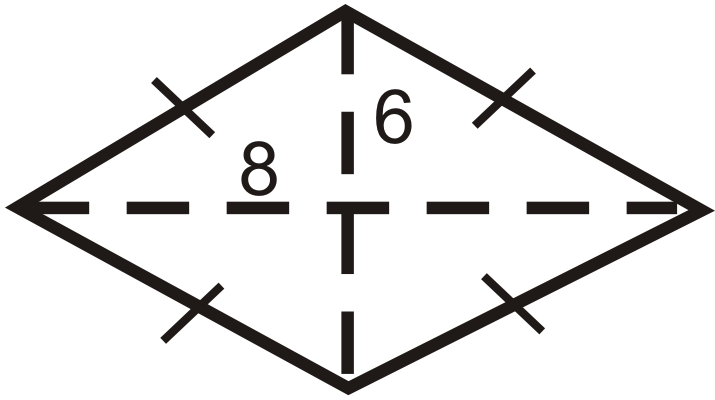
  播放段落

  Find the area of a rhombus with diagonals of 6 in and 8 in.
  ::找到一个有6英寸和8英寸对角的暴风车区域。

  播放段落

  The area is $\begin{align*}\frac{1}{2}(8)(6)=24 \ in^2\end{align*}$ .
  ::区域为12(8)(6)=24英寸2。

  播放段落

  Example 3
  ::例3

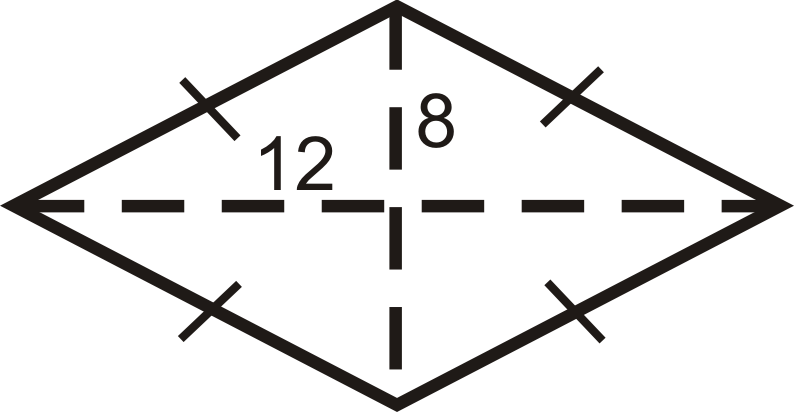
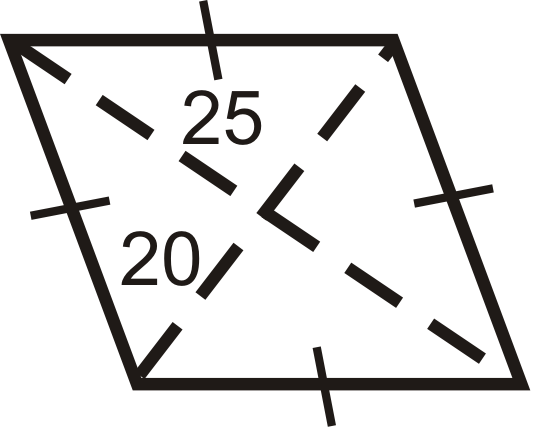
  播放段落

  Find the perimeter and area of the rhombus below.
  ::在下面找到暴风车的周界和地区

  

  播放段落

  In a rhombus, all four triangles created by the diagonals are congruent.
  ::在暴风雨中,对角形创造的所有四个三角形都是相似的。

  播放段落

  To find the perimeter, you must find the length of each side, which would be the hypotenuse of one of the four triangles. Use the Pythagorean Theorem.
  ::要找到周边, 您必须找到每边的长度, 也就是四个三角形中一个三角形的下限。 请使用 Pytagorian Theorem 。

  播放段落

  $$\begin{align*}12^2+8^2 &=side^2 && A=\frac{1}{2} \cdot 16 \cdot 24\\ 144+64 &= side^2 && A=192 \ units^2\\ side &= \sqrt{208}=4 \sqrt{13}\\ P &= 4 \left( 4\sqrt{13} \right)=16 \sqrt{13} \ units\end{align*}$$
  ::122+82=Side2A=121624144+64=Side2A=192 单位2side @208=413P=4(413)=1613

  播放段落

  Example 4
  ::例4

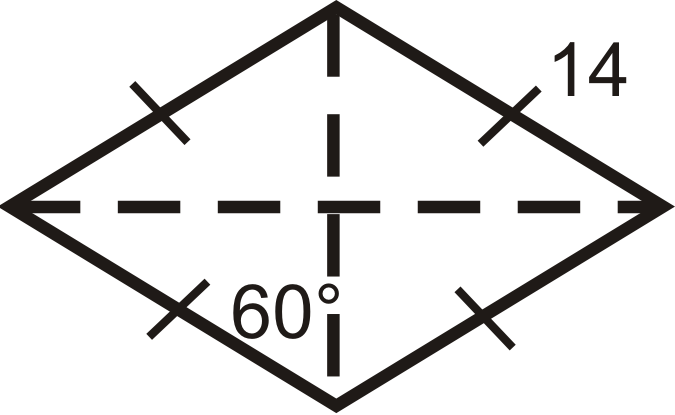
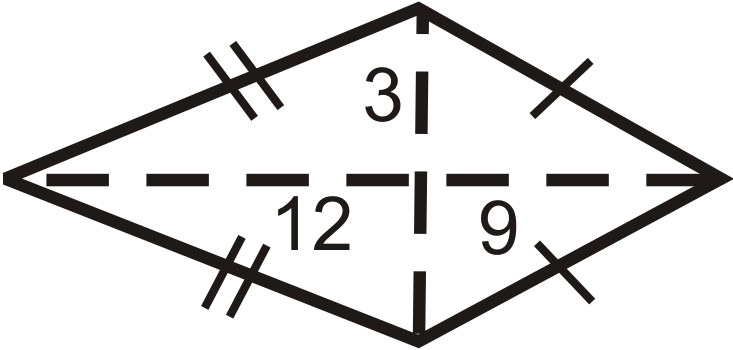
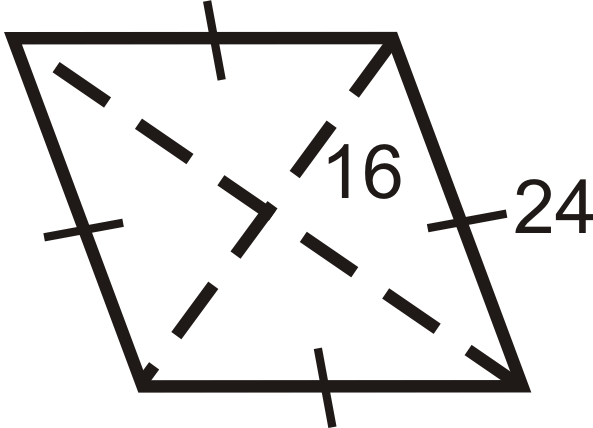
  播放段落

  Find the perimeter and area of the rhombus below.
  ::在下面找到暴风车的周界和地区

  

  播放段落

  In a rhombus, all four triangles created by the diagonals are congruent.
  ::在暴风雨中,对角形创造的所有四个三角形都是相似的。

  播放段落

  Here, each triangle is a 30-60-90 triangle with a hypotenuse of 14. From the special right triangle ratios the short leg is 7 and the long leg is $\begin{align*}7 \sqrt{3}\end{align*}$ .
  ::这里每个三角形是30-60-90三角形,下限为14。 从特殊的右三角形比率看,短腿为7,长腿为7。

  播放段落

  $$\begin{align*}P &= 4 \cdot 14=56 \ units && A=\frac{1}{2} \cdot 14 \cdot 14\sqrt{3}=98\sqrt{3} \ units^2\end{align*}$$
  ::P=414=56个单位A=1214143=983 2个单位

  播放段落

  Example 5
  ::例5

  播放段落

  The vertices of a quadrilateral are $\begin{align*}A(2, 8), B(7, 9), C(11, 2)\end{align*}$ , and $\begin{align*}D(3, 3)\end{align*}$ . Show $\begin{align*}ABCD\end{align*}$ is a kite and find its area.
  ::四边形的顶点是A(2,8,B(7,9,9),C(11,2)和D(3,3),显示ABCD是风筝,发现其区域。

  播放段落

  After plotting the points, it looks like a kite. $\begin{align*}AB = AD\end{align*}$ and $\begin{align*}BC = DC\end{align*}$ . The diagonals are perpendicular if the slopes are negative reciprocals of each other.
  ::在绘制点数后, 它看起来像一个风筝 。 AB= AD 和 BC=DC 。 如果斜坡是相互负对等的, 则对角是垂直的 。

  

  播放段落

  $$\begin{align*}m_{AC} &= \frac{2-8}{11-2}=-\frac{6}{9}=-\frac{2}{3}\\ m_{BD} &= \frac{9-3}{7-3}=\frac{6}{4}=\frac{3}{2}\end{align*}$$
  ::mAC=2-811-26923mBD=9-37-3=64=32

  播放段落

  The diagonals are perpendicular, so $\begin{align*}ABCD\end{align*}$ is a kite. To find the area, we need to find the length of the diagonals, AC and BD.
  ::对角线是垂直的, 所以ABCD是风筝。 要找到这个区域, 我们需要找到对角线、 AC 和 BD 的长度 。

  播放段落

  $$\begin{align*}d_1&= \sqrt{(2-11)^2+(8-2)^2} && d_2=\sqrt{(7-3)^2+(9-3)^2}\\ &= \sqrt{(-9)^2+6^2} && \quad =\sqrt{4^2+6^2}\\ &= \sqrt{81+36}=\sqrt{117}=3\sqrt{13} && \quad =\sqrt{16+36}=\sqrt{52}=2\sqrt{13}\end{align*}$$
  ::d1(2-11)2+(8-2)2d2(7-3)2+(9-3)2(9-2)2+(9)2+6242+6281+36117=313+16+36}52=213

  播放段落

  Plug these lengths into the area formula for a kite. $\begin{align*}A=\frac{1}{2} \left(3 \sqrt{13} \right)\left( 2\sqrt{13} \right)=39 \ units^2\end{align*}$
  ::A=12(313)(213)=39个单位2

  播放段落

  Review
  ::回顾

  播放段落
  1. Do you think all rhombi and kites with the same diagonal lengths have the same area? Explain your answer.
     ::你认为所有Rhombi和风筝的对角长度相同吗?请解释一下答案。

  播放段落

  Find the area of the following shapes. Round your answers to the nearest hundredth.
  ::查找以下形状的区域。 将您的答案绕到最近的一百位 。

  2. 

  3. 

  4. 

  5. 

  6. 

  7. 

  播放段落

  Find the area and perimeter of the following shapes. Round your answers to the nearest hundredth.
  ::查找以下形状的面积和周界。 将您的答案绕到最近的一百个形状 。

  8. 

  9. 

  10. 

  11. 

  播放段落

  For Questions 12 and 13, the area of a rhombus is $\begin{align*}32 \ units^2\end{align*}$ .
  ::关于问题12和13,暴客的面积为32个单位2。

  播放段落
  12. What would the product of the diagonals have to be for the area to be $\begin{align*}32 \ units^2\end{align*}$ ?
      ::对角线的产物是什么才能使这个区域达到32个单位2?
  播放段落
  13. List two possibilities for the length of the diagonals, based on your answer from #12.
      ::根据您在 #12 中的答复, 列出对角线长度的两种可能性 。

  播放段落

  For Questions 14 and 15, the area of a kite is $\begin{align*}54 \ units^2\end{align*}$ .
  ::对于问题14和15,风筝面积为54个单位2。

  播放段落
  14. What would the product of the diagonals have to be for the area to be $\begin{align*}54 \ units^2\end{align*}$ ?
      ::对角线的产物是什么才能使面积为54个单位2 ?
  播放段落
  15. List two possibilities for the length of the diagonals, based on your answer from #14.
      ::根据您在 #14 中的答复, 列出对角线长度的两种可能性 。

  播放段落

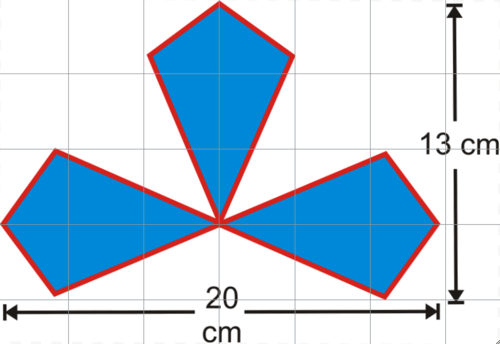
  Sherry designed the logo for a new company, made up of 3 congruent kites.
  ::雪莉为一家新公司设计了标志,由3个相同的风筝组成。

  播放段落
  16. What are the lengths of the diagonals for one kite? (Hint: use the long diagonal to find the length of shorter diagonal.)
      ::一个风筝的对角线长度是多少? (提示: 使用长对角线查找短对角线的长度 。 )
  播放段落
  17. Find the area of one kite.
      ::找到一只风筝的区域
  播放段落
  18. Find the area of the entire logo. 
      
      
      ::找到整个徽标的区域 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。