10.11 部门和部门面积

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 部门领域和部门领域

  Collapse Expand

  部门领域和部门领域

  播放段落

  Area of Sectors and Segments
  ::部门领域和部门领域

  播放段落

  A sector of a circle is the area bounded by two radii and the arc between the endpoints of the radii. If $\begin{align*}r\end{align*}$ is the radius and $\begin{align*}\widehat{AB}\end{align*}$ is the arc bounding a sector, then the area of the sector is $\begin{align*}A=\frac{m \widehat{AB}}{360^\circ} \cdot \pi r^2\end{align*}$ .
  ::一个圆的区块是受两个半径和半径端端点之间的弧线约束的区域。如果 r 是半径, AB 是段的弧线, 那么该区块的面积是 A=m AB360r2 。

  

  播放段落

  A segment of a circle is the area of a circle that is bounded by a chord and the arc with the same endpoints as the chord. The area of a segment is $\begin{align*}A_{segment}=A_{sector}-A_{\triangle ABC}\end{align*}$
  ::圆的某一段是圆的某一区域,圆的界线是带有和弦相同端点的和弦和弧之间的一个圆区域。

  

  播放段落

  What if you were given a circle with two radii in which the region between those two radii was shaded? How could you find the area of that shaded region of the circle?
  ::如果给您一个带两个半径的圆圈,让您看到这两个半径之间的区域是阴暗的,您如何找到圆的阴暗区域?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  The area of a sector is $\begin{align*}135 \pi\end{align*}$ and the arc measure is $\begin{align*}216^\circ\end{align*}$ . What is the radius of the circle?
  ::扇区面积为 135,弧度量为 216。圆的半径是多少?

  

  播放段落

  Plug in what you know to the sector area formula and solve for $\begin{align*}r\end{align*}$ .
  ::插入您所知道的 区域公式和 r 的解析 。

  播放段落

  $$\begin{align*}135 \pi &= \frac{216^\circ}{360^\circ} \cdot \pi r^2\\ 135 &= \frac{3}{5} \cdot r^2\\ \frac{5}{3} \cdot 135 &= r^2\\ 225 &= r^2 \rightarrow r=\sqrt{225}=15\end{align*}$$
  ::135216360r2135=35r253135=r2225=r2r225=15

  播放段落

  Example 2
  ::例2

  播放段落

  Find the area of the shaded region. The quadrilateral is a square .
  ::找到阴影区域的面积。 四方是方形 。

  

  播放段落

  The radius of the circle is 16, which is also half of the diagonal of the square. So, the diagonal is 32 and the sides would be $\begin{align*}\frac{32}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}=16 \sqrt{2}\end{align*}$ because each half of a square is a 45-45-90 triangle .
  ::圆的半径是 16, 也就是方形对角的半径。 因此, 方形是 32, 方形是 32 222 = 16 2, 因为方形的半角是 45- 45- 90 三角形 。

  播放段落

  $$\begin{align*}A_{circle} &= 16^2 \pi =256 \pi\\ A_{square} &= \left(16 \sqrt{2} \right)^2 = 256 \cdot 2=512\end{align*}$$
  ::轴=162256Asquare=(162)2=2562=512

  播放段落

  The area of the shaded region is $\begin{align*}256 \pi -512 \approx 292.25\end{align*}$
  ::阴暗区域面积为256 512 292.25。

  播放段落

  Example 3
  ::例3

  播放段落

  Find the area of the blue sector. Leave your answer in terms of $\begin{align*}\pi\end{align*}$ .
  ::找到蓝色部分的面积,请将答案保留在...

  

  播放段落

  In the picture, the central angle that corresponds with the sector is $\begin{align*}60^\circ\end{align*}$ . $\begin{align*}60^\circ\end{align*}$ is $\begin{align*}\frac{1}{6}\end{align*}$ of $\begin{align*}360^\circ\end{align*}$ , so this sector is $\begin{align*}\frac{1}{6}\end{align*}$ of the total area. $\begin{align*}area \ of \ blue \ sector=\frac{1}{6} \cdot \pi 8^2=\frac{32}{3} \pi\end{align*}$
  ::在图中,与这一部门相对应的中心角是60。 60是360中的16,因此这个部门是总面积的16。 蓝色部门面积=1682=323。

  播放段落

  Example 4
  ::例4

  播放段落

  The area of a sector is $\begin{align*}8\pi\end{align*}$ and the radius of the circle is 12. What is the central angle?
  ::扇区面积为 8,圆半径为 12。 中心角度是什么?

  播放段落

  Plug in what you know to the sector area formula and then solve for the central angle, which we will call $\begin{align*}x\end{align*}$ .
  ::插入您所知道的扇区公式, 然后解答中心角度, 我们称它为 x 。

  

  播放段落

  $$\begin{align*}8 \pi &= \frac{x}{360^\circ} \cdot \pi 12^2\\ 8 \pi & =\frac{x}{360^\circ} \cdot 144 \pi\\ 8 &= \frac{2x}{5^\circ}\\ x &= 8 \cdot \frac{5^\circ}{2}=20^\circ\end{align*}$$
  ::8x3601228x3601448=2x5x=8_52=20

  播放段落

  Example 5
  ::例5

  播放段落

  Find the area of the blue segment below.
  ::在下面找到蓝色段的区域。

  

  播放段落

  The area of the segment is the area of the sector minus the area of the isosceles triangle made by the radii. If we split the isosceles triangle in half, each half is a 30-60-90 triangle , where the radius is the hypotenuse . The height of $\begin{align*}\triangle ABC\end{align*}$ is 12 and the base is $\begin{align*}2 \left(12 \sqrt{3}\right)=24 \sqrt{3}\end{align*}$ .
  ::区段的面积是区区面积减去由半径制成的等骨质三角形区域。如果我们将等骨质三角形除以一半,则半径为30-60-90三角形,半径为下限。 QABC 高度为 12, 基数为 2( 12/13) = 24 3。

  播放段落

  $$\begin{align*}A_{sector} &= \frac{120}{360} \pi \cdot 24^2 && A_\triangle =\frac{1}{2} \left(24 \sqrt{3} \right)(12)\\ &= 192 \pi && \quad \ =144 \sqrt{3}\end{align*}$$
  ::A=120360242A12(243)(12)=192=1443

  播放段落

  The area of the segment is $\begin{align*}A=192 \pi - 144 \sqrt{3} \approx 353.8\end{align*}$ units.
  ::该段区域为A=1921443353.8单元。

  播放段落

  Review
  ::回顾

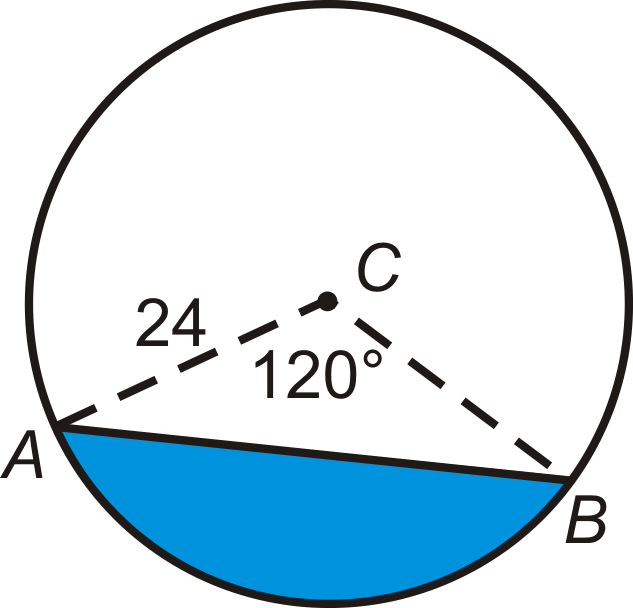
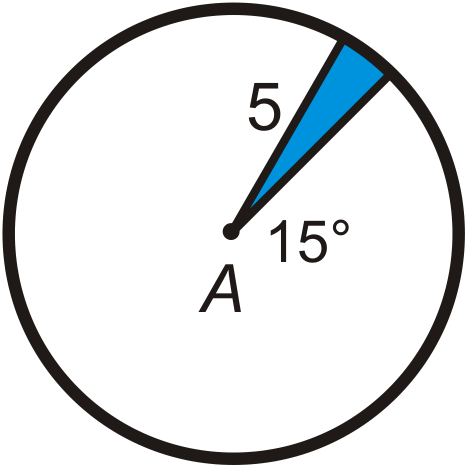
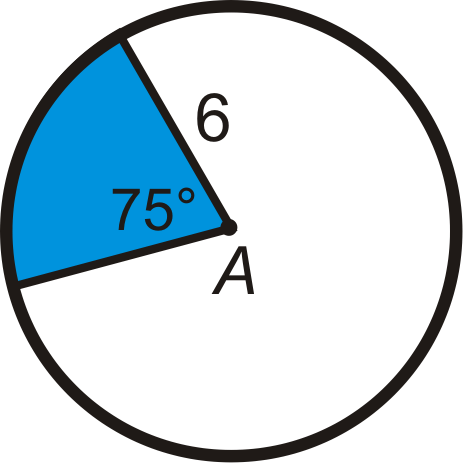
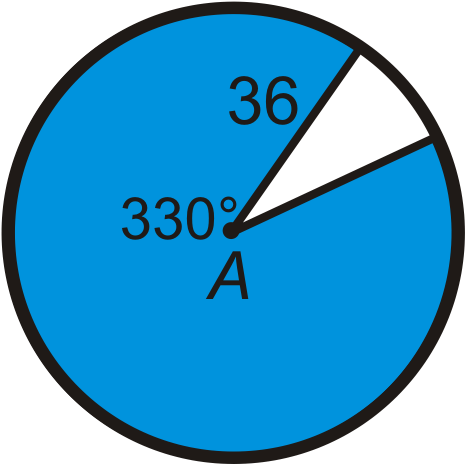
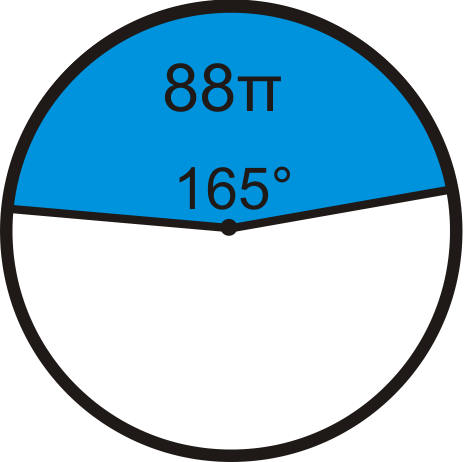
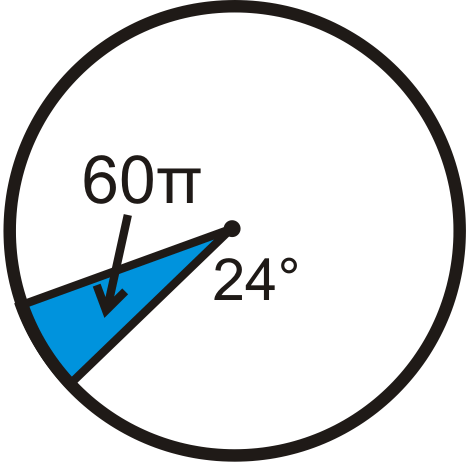
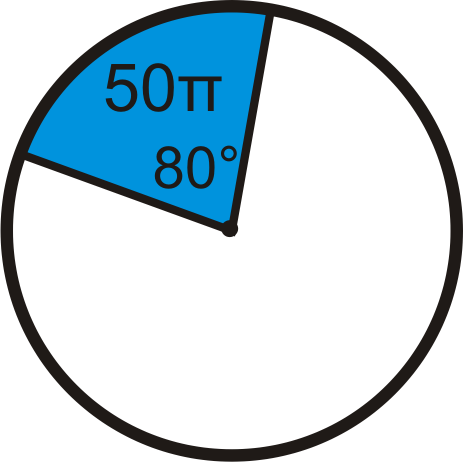
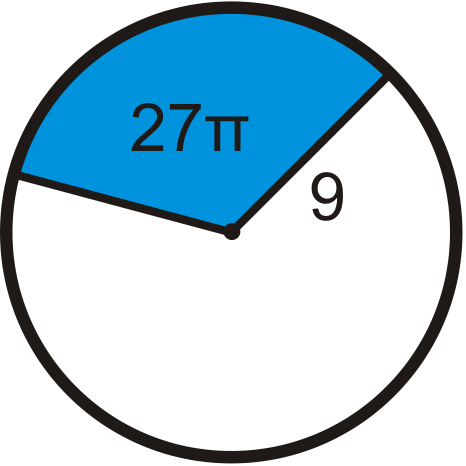
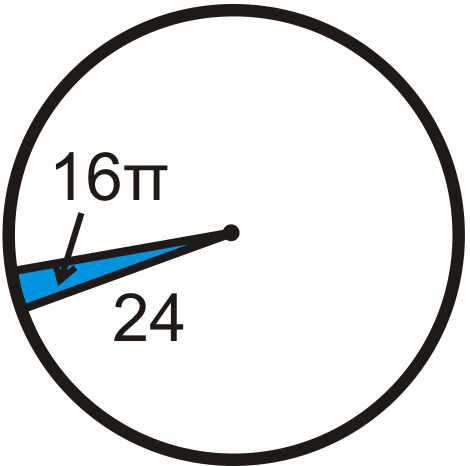
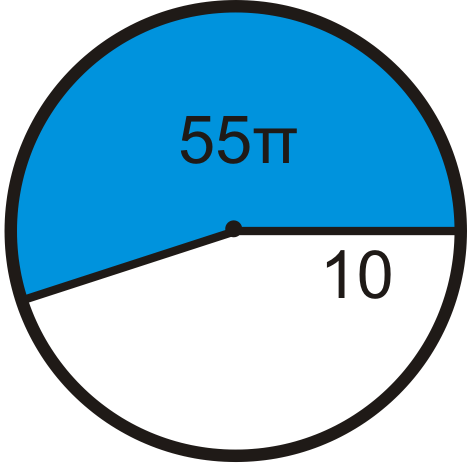
  播放段落

  Find the area of the blue sector or segment in $\begin{align*}\bigodot A\end{align*}$ . Leave your answers in terms of $\begin{align*}\pi\end{align*}$ . Round any decimal answers to the nearest hundredth.
  ::在 A 中查找蓝色扇区或区段的面积。 请保留您的答案为 。 将小数点后的任何答案按千位数四舍五入到最接近的百位 。

  1. 
  2. 
  3. 
  4. 
  5. 

  播放段落

  Find the radius of the circle. Leave your answer in terms of $\begin{align*}\pi\end{align*}$ .
  ::查找圆的半径。 请保留您的回答 。

  6. 
  7. 
  8. 

  播放段落

  Find the central angle of each blue sector. Round any decimal answers to the nearest tenth.
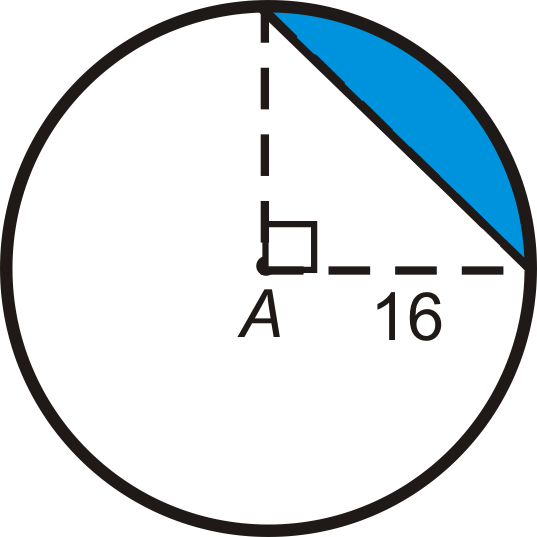
  ::查找每个蓝色区段的中心角度。 将小数点后的任何回答舍入到最接近的 10 点 。

  9. 
  10. 
  11. 

  播放段落

  Use the following image to answer questions 12 through 14. 
  ::使用以下图像回答问题12至14。

  播放段落
  12. 播放段落

      Find the area of the sector in  $\begin{align*}\bigodot A.\end{align*}$ Leave your answer in terms of  $\begin{align*}\pi.\end{align*}$
      ::在 A 中查找扇区区域。 请用 来回答 。

      
      ::在 A 中查找扇区区域。 请用 来回答 。
  播放段落
  13. Find the area of the equilateral triangle with side length 6.
      ::查找侧长6的等边三角形区域。
  播放段落
  14. Find the area of the blue segment. Round your answer to the nearest hundredth.
      ::找到蓝色段的面积。 将您的答复绕到最近的一百个区域 。

  播放段落

  Use the image to answer questions 15 through 17.
  ::使用图像回答问题15至17。

  播放段落
  15. Find the area of the sector in $\begin{align*}\bigodot A.\end{align*}$ Leave your answer in terms of  $\begin{align*}\pi.\end{align*}$  
      ::在 A 中查找扇区区域。 请用 来回答 。
  播放段落
  16. 播放段落

      Find the area of the right triangle.
      ::查找右三角形的区域 。

      
      ::查找右三角形的区域 。
  播放段落
  17. Find the area of the segment. Round your answer to the nearest hundredth.
      ::查找此段的区域。 将您的答案绕到最接近的一百个区域 。 @ info: whatsthis

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。