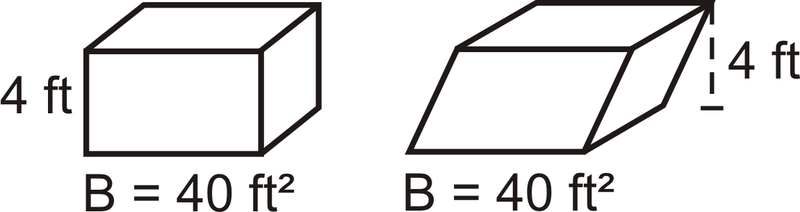11.3 棱晶

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 棱柱

  Collapse Expand

  棱柱

  播放段落

  Prisms
  ::棱柱

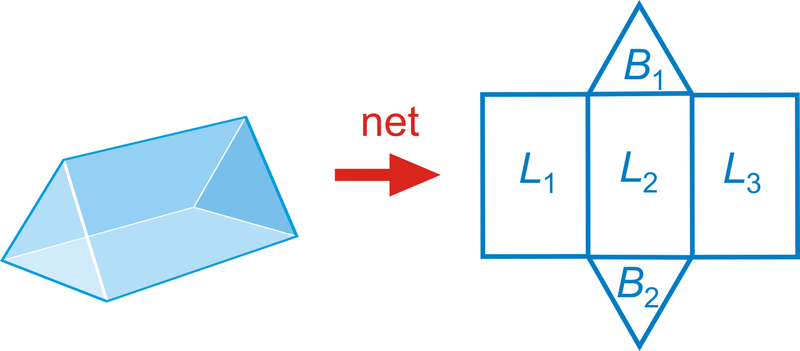
  播放段落

  A prism is a 3-dimensional figure with 2 congruent bases, in parallel planes, in which the other faces are .
  ::棱镜是一个三维的图象,在平行的平面上,有2个相容的基座,其他面孔在其中。

  播放段落

  The non-base faces are l ateral faces . The edges between the lateral faces are lateral edges .
  ::非 基 面 是 平 面 . 平 面 的 边缘 是 平 面 的 边缘

  播放段落

  This particular example is a pentagonal prism because its base is a pentagon . Prisms are named by the shape of their base. Prisms are classified as either right prisms (prisms where all the lateral faces are perpendicular to the bases) or oblique prisms (prisms that lean to one side, whose base is a rather than a rectangle , and whose height is perpendicular to the base's plane), as shown below.
  ::这个例子是一个五角形棱柱, 因为它的底部是五角形。 棱柱按其底部的形状命名。 棱柱被归类为右棱柱( 所有横向面孔都与底部垂直的棱柱) 或斜棱柱( 偏向一边的棱柱, 其底部是矩形而不是矩形, 其高度与底部平面垂直) , 如下所示 。

  

  播放段落

  Surface Area
  ::地表地区

  播放段落

  To find the of a prism, find the sum of the areas of its faces. The lateral area is the sum of the areas of the lateral faces. The basic unit of area is the square unit .
  ::为了找到棱镜, 找到其面部的总和。 平面区域是平面区域的总和。 基本区域单位是平方单位 。

  播放段落

  $$\begin{align*}Surface \ Area &= B_1+B_2+L_1+L_2+L_3\\ Lateral \ Area &= L_1+L_2+L_3\end{align*}$$
  ::表面面积=B1+B2+L1+L2+L2+L3LLLLATALLARTLARTL1+L2+LL3

  

  播放段落

  Volume
  ::量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量

  播放段落

  To find the of any solid you must figure out how much space it occupies. The basic unit of volume is the cubic unit.
  ::要找到任何固体,你必须弄清楚它占用了多少空间。基本体积单位是立方体单位。

  播放段落

  For prisms in particular, to find the volume you must find the area of the base and multiply it by the height.
  ::特别是对于棱晶来说, 要找到音量, 您必须找到基点的面积, 然后乘以它的高度 。

  播放段落

  Volume of a Prism: $\begin{align*}V=B \cdot h\end{align*}$ , where $\begin{align*}B=\end{align*}$  area of base.
  ::棱晶体积:V=Bh,B=基地区域。

  

  播放段落

  If an oblique prism and a right prism have the same base area and height, then they will have the same volume. This is due to Cavalieri’s Principle , which states that if two solids have the same height and the same cross-sectional area at every level, then they will have the same volume.
  ::如果斜面棱镜和右面棱镜有相同的基面积和高度,那么它们就会有相同的体积。 这要归功于卡瓦列里尼的原则。 该原则指出,如果两块固体在每一层都有相同的高度和相同的横截面面积,那么它们就会有相同的体积。

  

  播放段落

  What if you were given a solid three-dimensional figure with two congruent bases in which the other faces were rectangles? How could you determine how much two-dimensional and three-dimensional space that figure occupies?
  ::如果给了你一个坚固的三维图,它有两个相容的基点,使其他面孔成为矩形呢?你如何确定该图占据的二维和三维空间是多少?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  The total surface area of the triangular prism is $\begin{align*}540 \ units^2\end{align*}$ . What is $\begin{align*}x\end{align*}$ ?
  ::三角棱镜的表面总面积是540个单位2。 什么是 x?

  

  播放段落

  The total surface area is equal to:
  ::总表面面积等于:

  播放段落

  $$\begin{align*}A_{2 \ triangles}+A_{3 \ rectangles}=540\end{align*}$$
  ::A2 三角形+ A3 矩形= 540

  播放段落

  The hypotenuse of the triangle bases is 13, $\begin{align*}\sqrt{5^2+12^2}\end{align*}$ . Let’s fill in what we know.
  ::三角基点的时值为 13, 52+122。

  

  播放段落

  $$\begin{align*}A_{2 \ triangles} &= 2 \left(\frac{1}{2} \cdot 5 \cdot 12\right)=60\\ A_{3 \ rectangles} &= 5x+12x+13x=30x\\ 60+30x &= 540\\ 30x &= 480\\ x &= 16 \ units \qquad \text{The height is 16 units.}\end{align*}$$
  ::A2 三角形=2( 212=5) = 60A3 矩形=5x+12x+13x=30x60+30x=54030x=44030x=480x=480x=16单位

  播放段落

  Example 2
  ::例2

  播放段落

  Find the volume of the right rectangular prism below.
  ::在下面查找右侧矩形棱柱的体积。

  

  播放段落

  The area of the base is $\begin{align*}(5)(4)=20\end{align*}$ and the height is $\begin{align*}3\end{align*}$ . So the total volume is $\begin{align*}(20)(3)=60 \ units^3\end{align*}$
  ::基点区域为(5)(4)=20,高度为3。 所以总体积是(20(3)=60单位)3

  播放段落

  Example 3
  ::例3

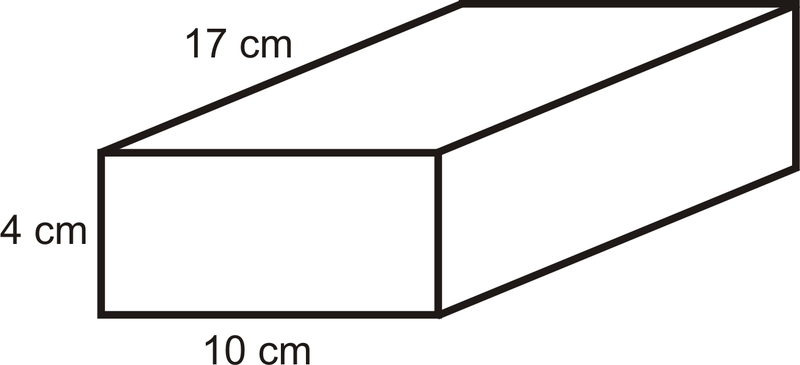
  播放段落

  Find the surface area of the prism below.
  ::找到下面棱晶的表面区域。

  

  播放段落

  To solve, draw the of the prism so that we can make sure we find the area of ALL faces.
  ::要解决,画出棱镜 这样我们才能找到 所有人的脸孔

  播放段落

  Using the net, we have:
  ::使用网,我们有:

  播放段落

  $$\begin{align*}SA_{prism} &= 2(4)(10)+2(10)(17)+2(17)(4)\\ &= 80+340+136\\ &= 556 \ cm^2\end{align*}$$
  ::Saprism=2(4)(4)(10)+2(10)(17+2(17(4)=80+340+136=556平方厘米)

  

  播放段落

  Example 4
  ::例4

  播放段落

  Find the surface area of the prism below.
  ::找到下面棱晶的表面区域。

  

  播放段落

  This is a right triangular prism. To find the surface area, we need to find the length of the hypotenuse of the base because it is the width of one of the lateral faces. We can use the Pythagorean Theorem to find this length.
  ::这是一个右三角棱柱。 要找到表面积, 我们需要找到基底的下限长度, 因为它是横向面的宽度 。 我们可以使用 Pythagorean 理论来找到这一长度 。

  

  播放段落

  $$\begin{align*}7^2+24^2 &= c^2\\ 49+576 &= c^2\\ 625 &= c^2 \qquad c=25\end{align*}$$
  ::72+242=c249+576=c2625=c2c=25

  播放段落

  Looking at the net, the surface area is:
  ::从网中看,地表面积如下:

  播放段落

  $$\begin{align*}SA &= 28(7)+28(24)+28(25)+2 \left(\frac{1}{2} \cdot 7 \cdot 24 \right)\\ SA &= 196+672+700+168=1736 \ units^2\end{align*}$$
  ::SA=196+672+700+168=1736单位2

  播放段落

  Example 5
  ::例5

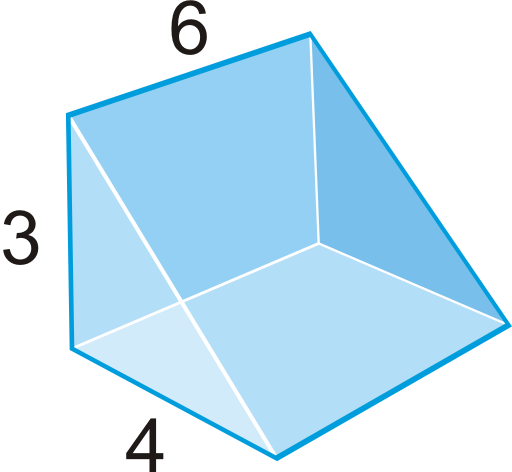
  播放段落

  You have a small, triangular prism-shaped tent. How much volume does it have once it is set up?
  ::你有一个小的三角棱晶形帐篷。一旦它被安装起来,它有多少量?

  

  播放段落

  First, we need to find the area of the base.
  ::首先,我们需要找到基地的面积。

  播放段落

  $$\begin{align*}B &= \frac{1}{2} (3)(4)=6 \ ft^2.\\ V &= Bh=6(7)=42 \ ft^3\end{align*}$$
  ::B=12(3)(4)=6 平方英尺2.V=Bh=6(7)=42平方英尺3

  播放段落

  Even though the height in this problem does not look like a “height,” it is because it is the perpendicular segment connecting the two bases.
  ::尽管这个问题的高度看起来不像“高度”,但这是因为它是连接两个基点的垂直部分。

  播放段落

  Review
  ::回顾

  播放段落
  1. What type of prism is this?
     ::这是什么类型的棱镜?
  播放段落
  2. Draw the net of this prism.
     ::绘制此棱镜的网格 。
  播放段落
  3. Find the area of the bases.
     ::找到基地的面积
  播放段落
  4. Find the surface area of all 4 lateral faces.
     ::找到所有4个横向面孔的表面积。
  播放段落
  5. Find the total surface area of the prism.
     ::查找棱镜的表面总面积 。

  播放段落
  6. How many one-inch cubes can fit into a box that is 8 inches wide, 10 inches long, and 12 inches tall? Is this the same as the volume of the box?
     ::有多少个一英寸的立方体能装在一个宽8英寸、10英寸长、12英寸高的盒子里?这和盒子的体积是一样的吗?
  播放段落
  7. A cereal box in 2 inches wide, 10 inches long and 14 inches tall. How much cereal does the box hold?
     ::2英寸宽的麦片盒,10英寸长,14英寸高。
  播放段落
  8. A can of soda is 4 inches tall and has a diameter of 2 inches. How much soda does the can hold? Round your answer to the nearest hundredth.
     ::苏打水罐高4英寸,直径为2英寸。可以支撑多少苏打水?将答案转至最近的100个。
  播放段落
  9. A cube holds $\begin{align*}216 \ in^3\end{align*}$ . What is the length of each edge?
     ::立方体持有216英寸3. 每边缘的长度是多少?
  播放段落
  10. A cube has sides that are 8 inches. What is the volume?
      ::立方体的边有8英寸,音量是多少?

  播放段落

  Use the right triangular prism to answer questions 11-15.
  ::使用右三角棱镜回答问题11-15。

  

  播放段落
  11. Find the volume of the prism.
      ::寻找棱镜的体积 。
  播放段落
  12. What shape are the bases of this prism? What are their areas?
      ::这个棱镜的底部是什么形状?
  播放段落
  13. What are the dimensions of each of the lateral faces? What are their areas?
      ::横向面孔的尺寸是多少?它们的面积是多少?
  播放段落
  14. Find the lateral surface area of the prism.
      ::寻找棱镜的横向表面区域 。
  播放段落
  15. Find the total surface area of the prism.
      ::查找棱镜的表面总面积 。
  播放段落
  16. Describe the difference between lateral surface area and total surface area.
      ::描述平面表面积和总表面面积之间的差别。
  播放段落
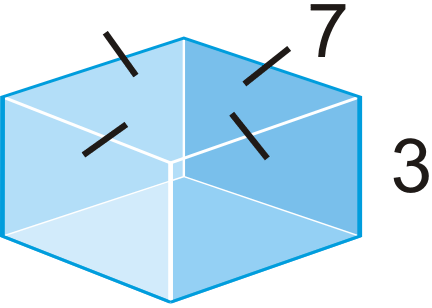
  17. Fuzzy dice are cubes with 4 inch sides.
      播放段落
      1. What is the volume and surface area of one die?
         ::一个死亡的体积和表面面积是多少?
      播放段落
      2. What is the volume and surface area of both dice?
         ::两个骰子的体积和表面面积是多少?
      
      ::模糊的骰子是四英寸边的立方体。 一个死亡的体积和表面面积是多少? 两个骰子的体积和表面面积是多少?

  播放段落

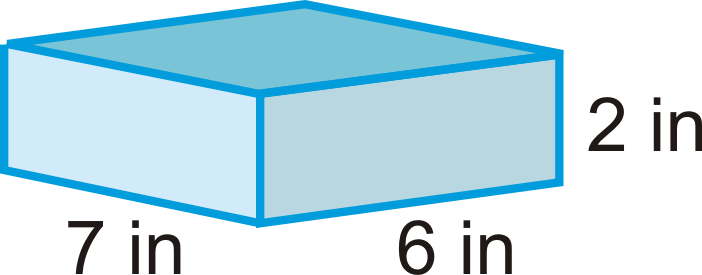
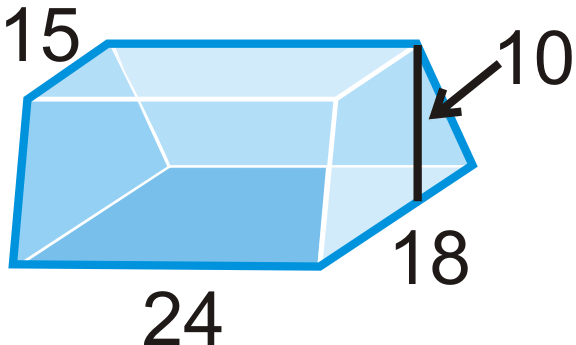
  Find the volume of the following solids. Round your answers to the nearest hundredth.
  ::查找以下固体的体积。 将您的答复转至最近的第一百个 。

  播放段落
  18. bases are isosceles trapezoids
      ::底座是等离子捕捉类
  19. 
  20. 
  21. 

  播放段落

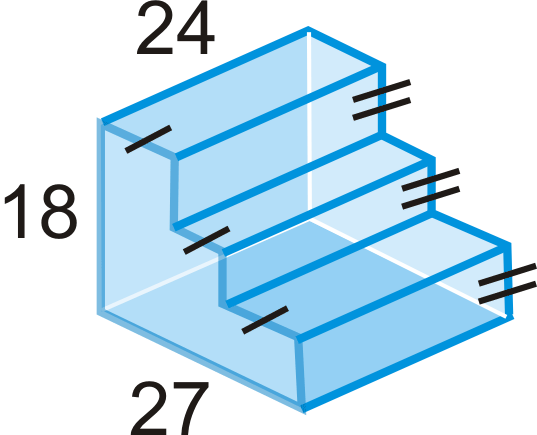
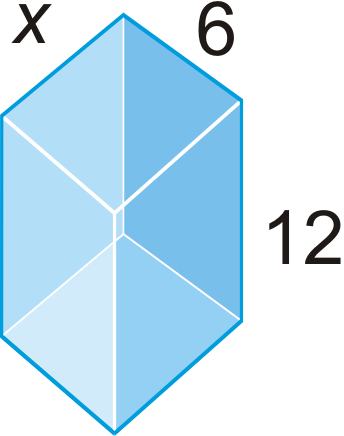
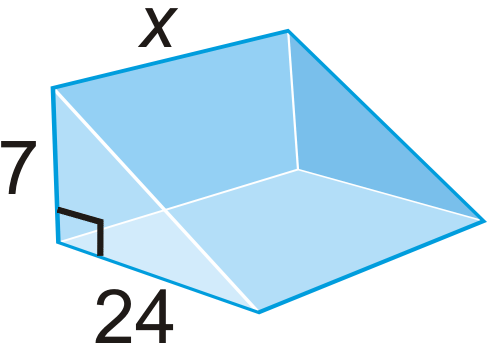
  Find the value of $\begin{align*}x\end{align*}$ , given the surface area.
  ::查找 x 值, 根据表面面积 。

  播放段落
  22. $\begin{align*}V=504 \ units^3\end{align*}$
      ::V=504个单位3
  播放段落
  23. $\begin{align*}V=2688 \ units^3\end{align*}$
      ::V=2688单位3

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。