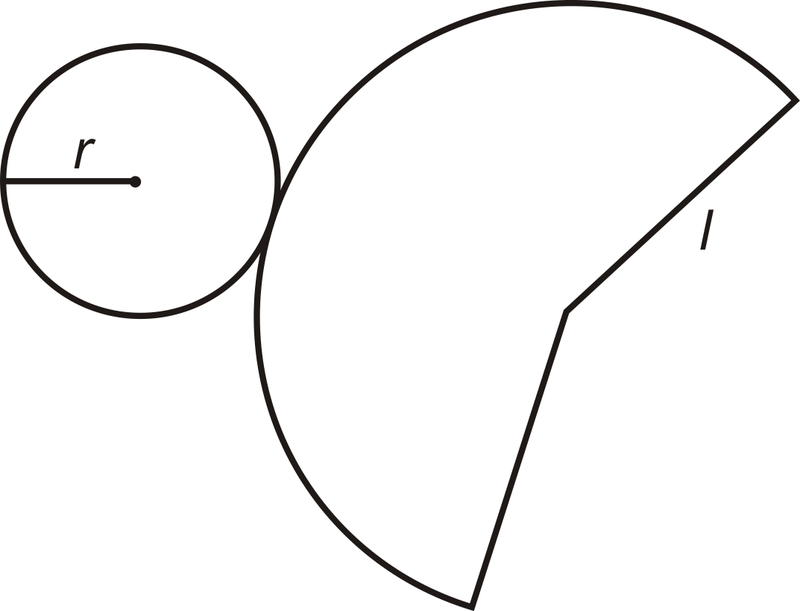11.6. 锥体

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 锥体

  Collapse Expand

  锥体

  播放段落

  Cones
  ::锥体

  播放段落

  A cone is a solid with a circular base and sides that taper up towards a vertex . A cone is generated from rotating a right triangle , around one leg. A cone has a slant height .
  ::锥体是圆形基座和斜面的固态。 锥体是由右三角旋转产生的, 围绕一条腿。 锥体有斜高 。

  

  播放段落

  Surface Area
  ::地表地区

  播放段落

  is a two-dimensional measurement that is the total area of all surfaces that bound a solid. The basic unit of area is the square unit . For the surface area of a cone we need the sum of the area of the base and the area of the sides.
  ::是一个二维的测量,是所有将固体捆绑在一起的表面的总面积。区域的基本单位是平方单位。对于锥体的表面区域,我们需要基数和两边面积的总和。

  播放段落

  Surface Area of a Right Cone: $\begin{array}{r}SA=\pi r^2+\pi rl\end{array}$ .
  ::右心线表面区域:SAr2rl。

  

  播放段落

  Area of the base: $\begin{array}{r}\pi r^2\end{array}$
  ::基地面积: °r2

  播放段落

  Area of the sides: $\begin{array}{r}\pi rl\end{array}$
  ::双方地区: rl

  播放段落

  Volume
  ::量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量

  播放段落

  To find the of any solid you must figure out how much space it occupies. The basic unit of volume is the cubic unit.
  ::要找到任何固体,你必须弄清楚它占用了多少空间。基本体积单位是立方体单位。

  播放段落

  Volume of a Cone: $\begin{array}{r}V=\frac{1}{3}\pi r^{2}h\end{array}$ .
  ::锥体体体积:V=13°r2h。

  

  播放段落

  What if you were given a three-dimensional with a circular base and sides that taper up towards a vertex? How could you determine how much two-dimensional and three-dimensional space that figure occupies?
  ::如果给了你一个三维的圆基和向顶端的侧面?你如何确定该数字占据了多少二维和三维空间?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  The surface area of a cone is $\begin{array}{r}36\pi \end{array}$ and the radius is 4 units. What is the slant height?
  ::锥体的表面面积是36°,半径是4个单位。倾斜高度是多少?

  播放段落

  Plug what you know into the formula for the surface area of a cone and solve for $\begin{array}{r}l\end{array}$ .
  ::将您所知道的信息插入锥形表面面积的公式中, 并解决 l 。

  播放段落

  $$\begin{array}{rl}36\pi & =\pi 4^2+\pi 4l\\ 36& =16+4lWheneachtermhasa\pi ,theycancelout.\\ 20& =4l\\ 5& =l\end{array}$$

  
  ::36424l36=16+4l 当每个学期有 ,它们取消20=4l5=l

  播放段落

  Example 2
  ::例2

  播放段落

  The volume of a cone is $\begin{array}{r}484\pi c{m}^3\end{array}$ and the height is 12 cm. What is the radius?
  ::锥体的体积是484厘米3,高度是12厘米。 半径是多少?

  

  播放段落

  Plug what you know to the volume formula.
  ::插入您所知道的音量公式 。

  播放段落

  $$\begin{array}{rl}484\pi & =\frac{1}{3}\pi r^2(12)\\ 121& =r^2\\ 11cm& =r\end{array}$$

  
  ::484138°r2(12)121=r211厘米=r

  播放段落

  Example 3
  ::例3

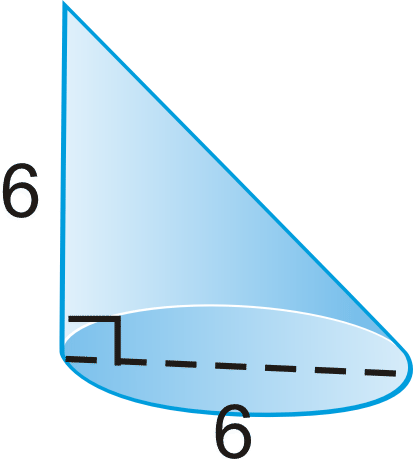
  播放段落

  What is the surface area of the cone?
  ::锥形的表面面积是多少?

  

  播放段落

  First, we need to find the slant height. Use the Pythagorean Theorem .
  ::首先,我们需要找到倾斜高度,使用毕达哥伦神话

  播放段落

  $$\begin{array}{rl}{l}^2& =9^2+{21}^2\\ & =81+441\\ l& =\sqrt{522}\approx 22.85\end{array}$$

  
  ::l2=92+212=81+441l=52222.85

  播放段落

  The total surface area, then, is $\begin{array}{r}SA=\pi 9^2+\pi (9)(22.85)\approx 900.54unit{s}^2\end{array}$ .
  ::因此,总面积为SA92(9)(22.85)900.54单位。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the volume of the cone.
  ::找到锥体的体积。

  

  播放段落

  First, we need the height. Use the Pythagorean Theorem.
  ::首先,我们需要高度,使用毕达哥伦神话

  播放段落

  $$\begin{array}{rl}{5}^2+h^2& ={15}^2\\ h& =\sqrt{200}=10\sqrt{2}\\ V& =\frac{1}{3}(5^2)\left(10\sqrt{2}\right)\pi \approx 370.24unit{s}^3\end{array}$$

  
  ::52+h2=152h=200=102V=13(52)(102)=370.243单位

  播放段落

  Example 5
  ::例5

  播放段落

  Find the volume of the cone.
  ::找到锥体的体积。

  

  播放段落

  We can use the same volume formula. Find the radius.
  ::我们可以使用相同的音量公式,找到半径

  播放段落

  $$\begin{array}{r}V=\frac{1}{3}\pi (3^2)(6)=18\pi \approx 56.55unit{s}^3\end{array}$$

  
  ::V=13(32)(6)=1856.55单位3

  播放段落

  Review
  ::回顾

  播放段落

  Use the cone to fill in the blanks.
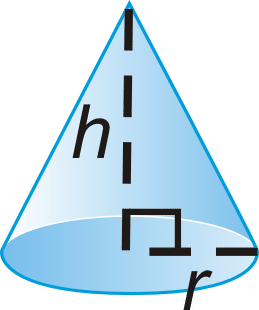
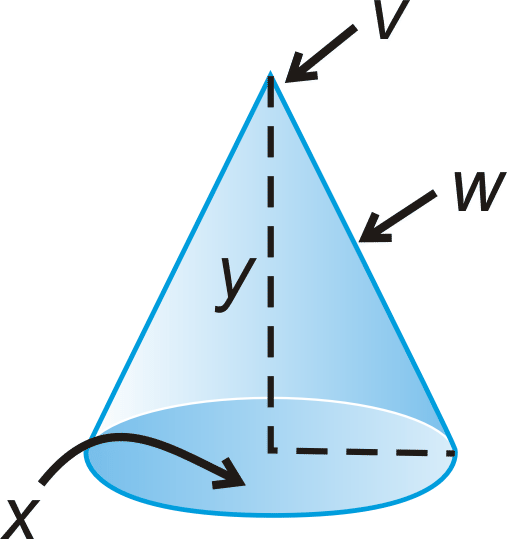
  ::用锥形填补空白。

  

  播放段落
  1. $\begin{array}{r}v\end{array}$ is the ___________.
     ::i 是 。
  播放段落
  2. The height of the cone is ______.
     ::锥体的高度是 。
  播放段落
  3. $\begin{array}{r}x\end{array}$ is a __________ and it is the ___________ of the cone.
     ::x 是 和 它是 的 锥 。
  播放段落
  4. $\begin{array}{r}w\end{array}$ is the _____________ ____________.
     ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}是的 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}是的 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}是的 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}是的 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

  播放段落

  Sketch the following solid and answer the question. Your drawing should be to scale, but not one-to-one. Leave your answer in simplest radical form.
  ::绘制下面的坚实和回答问题。 您的绘画应该是比例化的, 而不是一对一。 请将答案保留在最简单的激进形式上 。

  播放段落
  5. Draw a right cone with a radius of 5 cm and a height of 15 cm. What is the slant height?
     ::绘制半径为5厘米、高度为15厘米的右锥体。 斜度是多少?

  播放段落

  Find the slant height, $\begin{array}{r}l\end{array}$ , of one lateral face in the cone. Round your answer to the nearest hundredth.
  ::找到圆锥内侧面的倾斜高度, I。 将答案转至最近的一百位 。

  6. 

  播放段落

  Find the surface area and volume of the right cones. Round your answers to 2 decimal places.
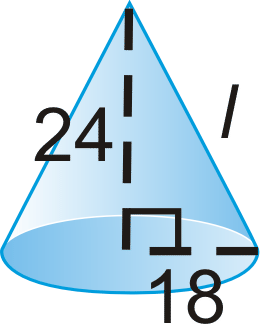
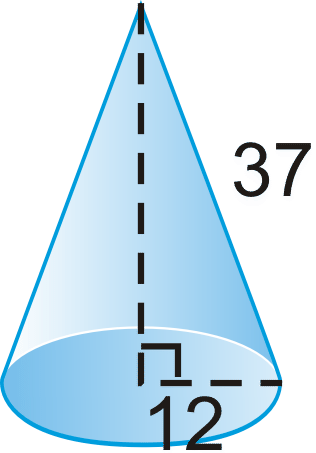
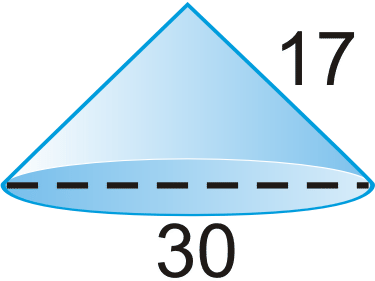
  ::查找右锥体的表面面积和体积。 将您的答复舍入到小数点后2位。

  7. 
  8. 
  播放段落
  9. If the lateral surface area of a cone is $\begin{array}{r}30\pi c{m}^2\end{array}$ and the radius is 5 cm, what is the slant height?
     ::如果锥体的横向表面面积为 30 cm cm2, 半径为 5 cm, 斜坡高度是多少 ?
  播放段落
  10. If the surface area of a cone is $\begin{array}{r}105\pi c{m}^2\end{array}$ and the slant height is 8 cm, what is the radius?
      ::如果锥体的表面面积是105°cm2,倾斜高度是8厘米,半径是多少?
  播放段落
  11. If the volume of a cone is $\begin{array}{r}30\pi c{m}^3\end{array}$ and the radius is 5 cm, what is the height?
      ::如果锥体的体积是 30 cm 3, 半径是 5 厘米, 高度是 多少 ?
  播放段落
  12. If the volume of a cone is $\begin{array}{r}105\pi c{m}^3\end{array}$ and the height is 35 cm, what is the radius?
      ::如果锥体的体积是105°Cm3,高度是35厘米,半径是多少?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。