课程： 3.15 三角公式和线性组合

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节三角公式和线性组合

折叠展开
三角公式和线性组合
In other lessons you've dealt with double angle formulas. This was useful for finding the value of an angle that was double your well known value. Now consider the idea of a "triple angle formula". If someone gave you a problem like this:
::在其他课程中, 您处理过双角度公式。这对于找到一个将您已知值翻倍的角值很有用。现在考虑一个“ 三角度公式” 的概念。如果有人给您这样的问题:

$\begin{align*}\sin 135^\circ\end{align*}$
::135 ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Could you compute its value?
::你能计算它的值吗?

Triple Angle Formulas and Linear Combinations
::三角公式和线性组合

Double angle formulas are great for computing the value of a trig function in certain cases. However, sometimes different multiples than two times and angle are desired. For example, it might be desirable to have three times the value of an angle to use as the argument of a trig function.
::在某些情况下,双角公式对于计算三重函数值来说是巨大的。但是,有时需要的倍数不同于两次,而角度则不同。例如,最好是将角值的三倍作为三重函数的参数。

By combining the sum formula and the double angle formula, formulas for triple angles and more can be found.
::通过将总和公式与双角公式相结合,可以找到三角度及更多角度的公式。

Here, we take an equation which takes a linear combination of and converts it into a simpler cosine function.
::在这里,我们用一个方程式, 将线性组合转换成更简单的余弦函数。

$\begin{align*}A \cos x + B \sin x = C \cos(x - D)\end{align*}$ , where $\begin{align*}C = \sqrt{A^2 + B^2}\end{align*}$ , $\begin{align*}\cos D = \frac{A}{C} \end{align*}$ and $\begin{align*}\sin D = \frac{B}{C}\end{align*}$ .
::Acosx+Bsinx=Ccos(x-D),C=A2+B2,cosD=AC和sinD=BC。

You can also use the TI-83 to solve trigonometric equations. It is sometimes easier than solving the equation algebraically. Just be careful with the directions and make sure your final answer is in the form that is called for. You calculator cannot put radians in terms of $\begin{align*}\pi\end{align*}$ .
::您也可以使用 TI- 83 来解析三角方程。有时比解析方程代数更容易。请小心方向, 并确保您的最终答案以需要的形式出现。您计算器不能用表示弧度。

Finding Formulas
::查找公式

Find the formula for $\begin{align*}\sin 3x \end{align*}$
::查找 sin3x 的公式

Use both the double angle formula and the sum formula.
::使用双角公式和总公式。

$\begin{aligned} \sin 3 x & = \sin (2 x + x) \\ = \sin (2 x) \cos x + \cos (2 x) \sin x \\ = (2 \sin x \cos x) \cos x + (\cos^{2} x - \sin^{2} x) \sin x \\ = 2 \sin x \cos^{2} x + \cos^{2} x \sin x - \sin^{3} x \\ = 3 \sin x \cos^{2} x - \sin^{3} x \\ = 3 \sin x (1 - \sin^{2} x) - \sin^{3} x \\ = 3 \sin x - 4 \sin^{3} x \end{aligned}$
$\begin{align*}\sin 3x &= \sin(2x + x) \\ &= \sin(2x) \cos x + \cos(2x)\sin x \\ &= (2 \sin x \cos x) \cos x + (\cos^2 x - \sin^2 x) \sin x \\ &= 2 \sin x \cos^2 x + \cos^2 x \sin x - \sin^3 x \\ &= 3 \sin x \cos^2 x - \sin^3 x \\ &= 3 \sin x(1 - \sin^2 x) - \sin^3 x \\ &= 3 \sin x - 4 \sin^3 x \end{align*}$
:2xxxx) =sin xxxxx3xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx2xxxxxxxxin2xxxxxxxxin3xxxxxin*xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx3xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx

Performing Transformations
::进行变换

Transform $\begin{align*}3 \cos 2x - 4 \sin 2x\end{align*}$ into the form $\begin{align*}C \cos(2x - D)\end{align*}$
::变换 3cos%2x- 4sin%2x 成 Ccos( 2x- D) 窗体

$\begin{align*}A = 3\end{align*}$ and $\begin{align*}B = -4\end{align*}$ , so $\begin{align*}C = \sqrt{3^2 + (-4)^2} = 5 \end{align*}$ . Therefore $\begin{align*} \cos D = \frac{3}{5}\end{align*}$ and $\begin{align*} \sin D = - \frac{4}{5}\end{align*}$ which makes the reference angle is $\begin{align*}-53.1^\circ\end{align*}$ or $\begin{align*}-0.927\end{align*}$ radians. since cosine is positive and sine is negative, the angle must be a fourth quadrant angle. $\begin{align*}D\end{align*}$ must therefore be $\begin{align*}306.9^ \circ\end{align*}$ or 5.36 radians. The final answer is $\begin{align*}3 \cos 2x - 4 \sin 2x = 5 \cos (2x - 5.36)\end{align*}$ .
::A=3和B4、C=32+(- 4)2=5. 因此,C=32+(- 4)2=5. 因此,C=D=35和sin=35和sin=D45 使参考角为-53.1或-0. 927弧度。由于正弦是正弦是正弦是负的,角度必须是第四个四角。因此,D必须是306.9或5.36弧度。最后答案是 3cos=2x4sin2x=5cos(2x-536)。

Solving for Unknown Values
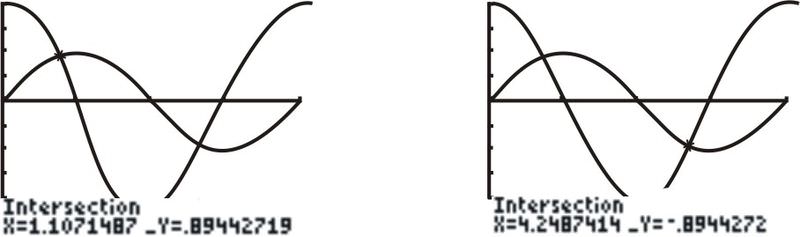
::解决未知值

Solve $\begin{align*}\sin x = 2 \cos x\end{align*}$ such that $\begin{align*}0 \le x \le 2\pi\end{align*}$ using a graphing calculator.
::使用图形化计算器解决 sinx=2cosx, 相当于 0x2。

Solution: In $\begin{align*}y =\end{align*}$ , graph $\begin{align*}y1 = \sin x\end{align*}$ and $\begin{align*}y2 = 2 \cos x\end{align*}$ .
::解析度: 在 y = 中, 图 y1 = sinx 和 y2 = 2cosx 。

Next, use CALC to find the intersection points of the graphs.
::接下来,使用 CALC 查找图形的交叉点。

Examples
::实例

Example 1
::例1

Earlier, you were asked to solve 135°.
::早些时候,你被要求解开135度

Using the triple angle formula we learned in this lesson for the sine function, we can break the angle down into three times a well known angle:
::使用我们从这个教训中学到的三重角度公式来计算正弦函数, 我们可以把角度拆成三倍一个众所周知的角度:

$\begin{align*}\sin 3x = 3 \sin x - 4 \sin^3 x \end{align*}$
::3x=3sin *x -4sin3*x

we can solve this problem.
::我们可以解决这个问题。

$\begin{aligned} \sin (3 \times 45^{\circ}) = 3 \sin 45^{\circ} - 4 \sin^{3} 45^{\circ} \\ = 3 \frac{\sqrt{2}}{2} - 4 {(\frac{\sqrt{2}}{2})}^{3} \\ = 3 \frac{\sqrt{2}}{2} - (\frac{4 (2)^{2 / 3}}{8}) \\ = \frac{3 \sqrt{2} - 2 \sqrt{2}}{2} \\ = \frac{\sqrt{2}}{2} \end{aligned}$
$\begin{align*} \sin(3 \times 45^\circ) = 3 \sin 45^\circ - 4 \sin^3 45^\circ\\ =3 \frac{\sqrt{2}}{2} - 4 \left(\frac{\sqrt{2}}{2} \right)^3\\ =3 \frac{\sqrt{2}}{2} - \left( \frac{4(2)^{2/3}}{8} \right)\\ =\frac{3\sqrt{2} - 2\sqrt{2}}{2}\\ =\frac{\sqrt{2}}{2}\\ \end{align*}$
::3×45)=3sin454sin34534532-2-44(22)3=322-(4(2)2/38)=32-222=22

Example 2
::例2

Transform $\begin{align*}\ 5 \cos x - 5 \sin x\end{align*}$ to the form $\begin{align*}C \cos(x - D)\end{align*}$
::变换 5cosx- 5sinx 至 Ccos(x- D) 窗体

If $\begin{align*}5 \cos x - 5 \sin x\end{align*}$ , then $\begin{align*}A = 5\end{align*}$ and $\begin{align*}B = -5\end{align*}$ . By the , $\begin{align*}C = 5 \sqrt{2}\end{align*}$ and $\begin{align*}\cos D = \frac{5}{5 \sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\end{align*}$ . So, because $\begin{align*}B\end{align*}$ is negative, $\begin{align*}D\end{align*}$ is in Quadrant IV. Therefore, $\begin{align*}D = \frac{7 \pi}{4}\end{align*}$ . Our final answer is $\begin{align*}5 \sqrt{2} \cos \left (x - \frac{7 \pi}{4} \right)\end{align*}$ .
::如果 5cosx- 5sinx, 那么 A=5 和 B5. , by the, C=52 and cosD= 552=12=22. 所以, 因为 B 是负的, D 在 Quadrant IV。因此, D= 74。我们的最后一个答案是 52cos(x- 74)。

Example 3
::例3

Transform $\begin{align*} - 15 \cos 3x - 8 \sin 3x \end{align*}$ to the form $\begin{align*}C \cos(x - D)\end{align*}$
::变换 - 15cos3x-8sin3x 至 Ccos(x- D) 窗体

If $\begin{align*}-15 \cos 3x - 8 \sin 3x\end{align*}$ , then $\begin{align*}A = -15\end{align*}$ and $\begin{align*}B = -8\end{align*}$ . By the Pythagorean Theorem, $\begin{align*}C = 17\end{align*}$ . Because $\begin{align*}A\end{align*}$ and $\begin{align*}B\end{align*}$ are both negative, $\begin{align*}D\end{align*}$ is in Quadrant III, which means $\begin{align*}D = \cos^{-1} \left (\frac{15}{17} \right) = 0.49+\pi = 3.63\end{align*}$ rad . Our final answer is $\begin{align*}17 \cos 3(x - 3.63)\end{align*}$ .
::如果 -15cos=3x-8sin=3x,然后是A15和B8。根据Pythagorean理论,C=17。由于A和B都是负数,D在Quadrant III中,这意味着D=cos-1(1517=0.49}3.63rad。我们的最后答案是17cos}3(x-3.633)。

Example 4
::例4

Derive a formula for $\begin{align*}\tan 4x\end{align*}$ .
::绘制一种 tan4x 的公式。

$\begin{aligned} \tan 4 x & = \tan (2 x + 2 x) \\ = \frac{\tan 2 x + \tan 2 x}{1 - \tan 2 x \tan 2 x} \\ = \frac{2 \tan 2 x}{1 - \tan^{2} 2 x} \\ = \frac{2 \cdot \frac{2 \tan x}{1 - \tan^{2} x}}{1 - {(\frac{2 \tan x}{1 - \tan^{2} x})}^{2}} \\ = \frac{4 \tan x}{1 - \tan^{2} x} \div \frac{(1 - \tan^{2} x)^{2} - 4 \tan^{2} x}{(1 - \tan^{2} x)^{2}} \\ = \frac{4 \tan x}{1 - \tan^{2} x} \div \frac{1 - 2 \tan^{2} x + \tan^{4} x - 4 \tan^{2} x}{(1 - \tan^{2} x)^{2}} \\ = \frac{4 \tan x}{1 - \tan^{2} x} \cdot \frac{(1 - \tan^{2} x)^{2}}{1 - 6 \tan^{2} x + \tan^{4} x} \\ = \frac{4 \tan x - 4 \tan^{3} x}{1 - 6 \tan^{2} x + \tan^{4} x} \end{aligned}$
$\begin{align*}\tan 4x &= \tan (2x + 2x)\\ &= \frac {\tan 2x + \tan 2x}{1 - \tan 2x \tan 2x}\\ &= \frac {2 \tan 2x}{1 - \tan^2 2x}\\ &= \frac{2 \cdot \frac{2 \tan x}{1 - \tan^2x}}{1 - \left ( \frac{2 \tan x}{1 - \tan^2x} \right )^2}\\ &= \frac{4 \tan x}{1 - \tan^2 x} \div \frac{(1 - \tan ^2 x)^2 - 4 \tan^2 x}{(1 - \tan^2 x)^2}\\ &= \frac{4 \tan x}{1 - \tan^2 x} \div \frac{1 - 2 \tan^2 x + \tan^4 x- 4 \tan^2 x}{(1 - \tan^2 x)^2}\\ &= \frac{4 \tan x}{1 - \tan^2 x} \cdot \frac{(1 - \tan^2 x)^2}{1 - 6 \tan^2 x + \tan^4 x}\\ &= \frac{4 \tan x - 4 \tan^3 x}{1 - 6 \tan^2 x + \tan^4 x}\end{align*}$
::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Review
::回顾

Transform each expression to the form $\begin{align*}C \cos(x - D)\end{align*}$ .
::将每个表达式转换为 Ccos(x-D) 窗体。

$\begin{align*}3\cos x - 2 \sin x\end{align*}$
::3cosx- 2sinx

$\begin{align*}2\cos x - \sin x\end{align*}$
::2cosx-sinx

$\begin{align*}-4\cos x + 5 \sin x\end{align*}$
::-4cosx+5sinx

$\begin{align*}7\cos x - 6 \sin x\end{align*}$
::7cosx- 6sinx

$\begin{align*}11\cos x + 9 \sin x\end{align*}$
::11cosx+9sinx

$\begin{align*}14\cos x + 2 \sin x\end{align*}$
::14cosx+2sinx

$\begin{align*}-2\cos x - 4 \sin x\end{align*}$
::-2cosx -4sinx

Derive a formula for each expression.
::为每个表达式绘制一个公式。

$\begin{align*}\sin 4x\end{align*}$
::sin 4x( sin 4x)

$\begin{align*}\cos 6x\end{align*}$
::COs=6x COs=6x

$\begin{align*}\cos 4x\end{align*}$
::COs=4x COs=4x

$\begin{align*}\csc 2x\end{align*}$
::csc%2x

$\begin{align*}\cot 2x\end{align*}$
::comt2x

Find all solutions to each equation in the interval $\begin{align*}[0,2\pi)\end{align*}$ .
::在间隔 [0,2] 中找到每个方程式的所有解决方案。

$\begin{align*}\cos x +\cos 3x=0\end{align*}$
::COSx+COS3x=0

$\begin{align*}\sin 2x =\cos 3x\end{align*}$
::sin *% 2x=cos *3x

$\begin{align*}\cos 2x +\cos 4x=0\end{align*}$
::COs=0 =2x+cos=0 =2x+cos=0

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

三角公式和线性组合

Triple Angle Formulas and Linear Combinations ::三角公式和线性组合

Finding Formulas ::查找公式

Performing Transformations ::进行变换

Solving for Unknown Values ::解决未知值

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Triple Angle Formulas and Linear Combinations
::三角公式和线性组合

Finding Formulas
::查找公式

Performing Transformations
::进行变换

Solving for Unknown Values
::解决未知值

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)