12.2 轮调对称

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 旋转对称

  Collapse Expand

  旋转对称

  播放段落

  Rotation Symmetry
  ::旋转对称

  播放段落

  Rotational symmetry is present when a figure can be rotated (less than $\begin{array}{r}{360}^{\circ }\end{array}$ ) such that it looks like it did before the rotation . The center of rotation is the point a figure is rotated around such that the rotational symmetry holds.
  ::当一个数字可以旋转( 小于 360 ) 时, 就会出现旋转对称, 这样它看起来就像在旋转之前一样。 旋转的中心是某个数字在旋转对称时旋转的点, 这样可以保持旋转对称 。

  

  播放段落

  For the $\begin{array}{r}H\end{array}$ , we can rotate it twice, the triangle can be rotated 3 times and still look the same and the hexagon can be rotated 6 times.
  ::对于H,我们可以旋转它两次,三角形可以旋转3次,看起来仍然一样,六边形可以旋转6次。

  播放段落

  What if you had a six-pointed star and you rotated that star less than $\begin{array}{r}{360}^{\circ }\end{array}$ ? If the rotated star looked exactly the same as the original star, what would that say about the star?
  ::如果你有一个六点的恒星,而你旋转的恒星小于360?如果旋转的恒星与原恒星看起来完全一样,那会如何?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Determine if the figure below has rotational symmetry. Find the angle and how many times it can be rotated.
  ::确定下图是否具有旋转对称。 查找角度, 以及可以旋转多少次 。

  

  播放段落

  The pentagon can be rotated 5 times. Because there are 5 lines of rotational symmetry, the angle would be $\begin{array}{r}\frac{{360}^{\circ }}{5}={72}^{\circ }\end{array}$ .
  ::五边形可以旋转5次。 因为有5条旋转对称线, 角度将是3605=72。

  

  

  播放段落

  Example 2
  ::例2

  播放段落

  Determine if the figure below has rotational symmetry. Find the angle and how many times it can be rotated.
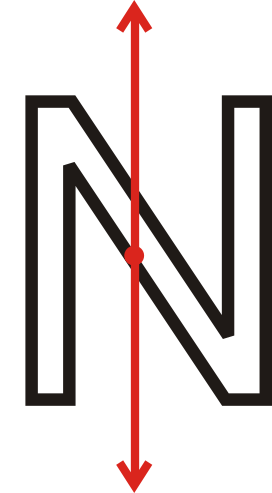
  ::确定下图是否具有旋转对称。 查找角度, 以及可以旋转多少次 。

  

  播放段落

  The $\begin{array}{r}N\end{array}$ can be rotated twice. This means the angle of rotation is $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::N可旋转两次。 这意味着旋转的角度是180。

  

  播放段落

  Example 3
  ::例3

  播放段落

  Determine if the figure below has rotational symmetry. Find the angle and how many times it can be rotated.
  ::确定下图是否具有旋转对称。 查找角度, 以及可以旋转多少次 。

  

  播放段落

  The checkerboard can be rotated 4 times. There are 4 lines of rotational symmetry, so the angle of rotation is $\begin{array}{r}\frac{{360}^{\circ }}{4}={90}^{\circ }\end{array}$ .
  ::棋盘可以旋转 4 次 。 有 4 条旋转对称线, 因此旋转的角度是 360 4 = 90 。

  

  

  播放段落

  Example 4
  ::例4

  播放段落

  Find the angle of rotation and the number of times each figure can rotate.
  ::查找旋转角度和每个数字可以旋转的次数。

  

  播放段落

  The can be rotated twice. The angle of rotation is $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::旋转角度是180。

  播放段落

  Example 5
  ::例5

  

  播放段落

  The hexagon can be rotated six times. The angle of rotation is $\begin{array}{r}{60}^{\circ }\end{array}$ .
  ::六边形可以旋转六倍。旋转的角度是 60。

  播放段落

  Review
  ::回顾

  播放段落
  1. If a figure has 3 lines of rotational symmetry, it can be rotated _______ times.
     ::如果一个数字有3条旋转对称线,可以旋转%倍。
  播放段落
  2. If a figure can be rotated 6 times, it has _______ lines of rotational symmetry.
     ::如果一个数字可以旋转6次,它具有旋转对称线。
  播放段落
  3. If a figure can be rotated $\begin{array}{r}n\end{array}$ times, it has _______ lines of rotational symmetry.
     ::如果一个数字可以旋转 n 次, 则具有旋转对称的线条 。
  播放段落
  4. To find the angle of rotation, divide $\begin{array}{r}{360}^{\circ }\end{array}$ by the total number of _____________.
     ::要找到旋转角度, 将360++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
  播放段落
  5. Every square has an angle of rotation of _________.
     ::每个广场的旋转角度都是 。

  播放段落

  Determine whether each statement is true or false.
  ::确定每一声明是真实的还是虚假的。

  播放段落
  6. Every parallelogram has rotational symmetry.
     ::每个平行图都有旋转对称。
  播放段落
  7. Every figure that has line symmetry also has rotational symmetry.
     ::每个有线对称的数字也都有旋转对称。

  播放段落

  Determine whether the words below have rotation symmetry.
  ::确定以下单词是否具有旋转对称性。

  播放段落
  8. OHIO
     ::俄、俄、俄、俄、俄、俄、俄
  播放段落
  9. MOW
     ::呜
  播放段落
  10. WOW
      ::哇哇
  播放段落
  11. KICK
      ::鸡鸡
  播放段落
  12. pod
      ::缓冲

  播放段落

  Find the angle of rotation and the number of times each figure can rotate.
  ::查找旋转角度和每个数字可以旋转的次数。

  13. 
  14. 
  15. 

  播放段落

  Determine if the figures below have rotation symmetry. Identify the angle of rotation.
  ::确定下图是否具有旋转对称。 指定旋转角度 。

  16. 
  17. 
  18. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。