4.1 三角比率逆数定义

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 三角比率逆数定义

  Collapse Expand

  三角比率逆数定义

  播放段落

  You are in band practice one day when something catches your eye. One of your fellow students has a musical instrument that you haven't seen played before - a triangle. This is an instrument that is a metal triangle that the musician plays by striking it. Walking over to your classmate, you ask him about the instrument. During a conversation about the triangle, you wonder if it would be possible to make different types of triangle instruments to make different sounds. 
  ::当某事触目惊心时,你将参加乐队练习。你的同学之一拥有一种你以前从未见过的乐器, 一个三角形。 这是一个音乐家通过敲击它来玩的金属三角形乐器。 走到你的同学面前, 你问他关于乐器的事。 在关于三角形的谈话中, 你想知道是否有可能制作不同类型三角形乐器来发出不同的声音 。

  播放段落

  You ask your science teacher about this, and she is excited that you have taken an interest in the topic. Together you decide to devise some new instruments based on different length sides of triangles, and then try them out to see how they sound. To begin, your teacher asks you to create a list of a few different sides of triangle lengths, and then list the interior angles of the triangles you come up with.
  ::你问科学老师这个问题,她很兴奋你对这个话题感兴趣。你们一起决定设计一些基于三角形不同长边的新仪器,然后试一下它们,看看它们的声音。首先,老师要求你们建立一个三角形不同边的列表,然后列出三角形的内部角度。

  播放段落

  You immediately get to work and generate a list. The first triangle has sides of 12 cm, 35 cm, and 37 cm, and is a right triangle. However, you realize that you aren't sure of the interior angles of the triangles. You are about to get out a paper and pencil to start plotting the triangles when you start to wonder if there might be an easier way to use math in finding the measurement of the angles instead of plotting them and measuring by hand.
  ::您立即开始工作并生成列表。 第一个三角形的侧面为 12 cm, 35 cm, 37 cm, 是一个右三角形。 然而, 您意识到您并不确定三角形的内部角度。 当您开始思考是否有比较容易的方法使用数学来找到角度, 而不是用手来绘制和测量角度时, 您即将拿出一张纸和铅笔来绘制三角形 。

  播放段落

  Inverse of Trigonometric Ratios
  ::三角对数比率的逆数

  播放段落

  In this section, we'll discuss and apply examples of the for trig ratios.
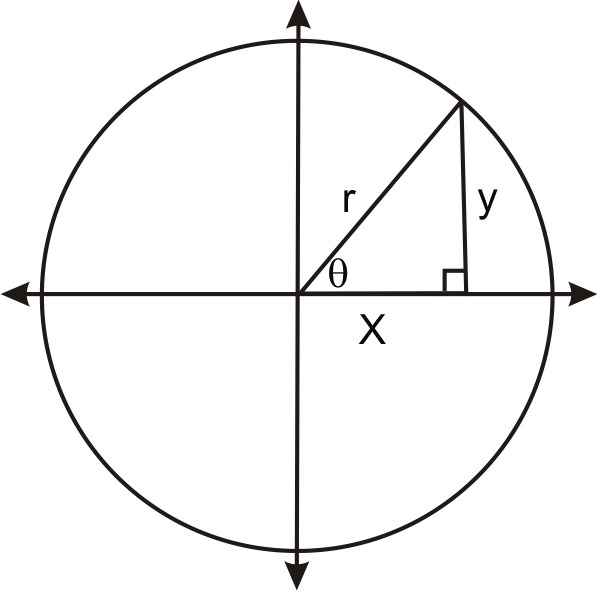
  ::在本节中,我们将讨论并应用三角比率的例子。

  播放段落

  Recall the ratios of the six trig functions and their inverses, with regard to the unit circle .
  ::回顾六个三角函数的比率及其相对于单位圆的反比。

  

  播放段落

  $$\begin{array}{r}\sin \theta =\frac{y}{r}\to {\sin }^{-1}\frac{y}{r}=\theta \cos \theta =\frac{x}{r}\to {\cos }^{-1}\frac{x}{r}=\theta \\ \tan \theta =\frac{y}{x}\to {\tan }^{-1}\frac{y}{x}=\theta \cot \theta =\frac{x}{y}\to {\cot }^{-1}\frac{x}{y}=\theta \\ \csc \theta =\frac{r}{y}\to {\csc }^{-1}\frac{r}{y}=\theta \sec \theta =\frac{r}{x}\to {\sec }^{-1}\frac{r}{x}=\theta \end{array}$$

  
  ::

  播放段落

  These ratios can be used to find any $\begin{array}{r}\theta \end{array}$ in standard position or in a triangle.
  ::这些比率可用于在标准位置或三角形中找到任何 。

  播放段落

  In a sense, this is a way of ‘‘undoing’’ a trig function. Before, to find a trig function, you would use the ratio of two sides. Now, by using the inverse trig ratio, you can find angles when you need them.
  ::从某种意义上说,这是一种“un doing” 三角函数的方式。在找到三角函数之前,您将使用两边的比。现在,通过使用反三角比,您可以在需要时找到角度。

  播放段落

  Let's look at some problems involving inverse trigonometric ratios. 
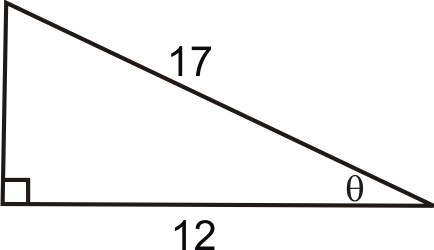
  ::让我们来看看一些问题 涉及逆三角比。

  播放段落

  1. Find the measure of the angles below.
  ::1. 找出以下角度的量度。

  

  播放段落

  You need to use the sine function, and then find the inverse of sine. 
  ::您需要使用正弦函数, 然后找到正弦的反函数 。

  播放段落

  $\begin{array}{r}\sin x=\frac{7}{25}\to {\sin }^{-1}\frac{7}{25}=x\to x={16.26}^{\circ }\end{array}$
  ::x=725sin -1725=xxx=16.26

  

  播放段落

  You need to use the tangent function, and then find the inverse of tangent. 
  ::您需要使用正切函数, 然后发现反正切值 。

  播放段落

  $\begin{array}{r}\tan x=\frac{40}{9}\to {\tan }^{-1}\frac{40}{9}=x\to x={77.32}^{\circ }\end{array}$
  ::-=====================================================================================================================================================================================================================

  播放段落

  The trigonometric value $\begin{array}{r}\tan \theta =\frac{40}{9}\end{array}$ of the angle is known, but not the angle. In this case the inverse of the trigonometric function must be used to determine the measure of the angle. The inverse of the tangent function is read “tangent inverse” and is also called the arctangent relation. The inverse of the cosine function is read “cosine inverse” and is also called the arccosine relation. The inverse of the sine function is read “sine inverse” and is also called the arcsine relation.
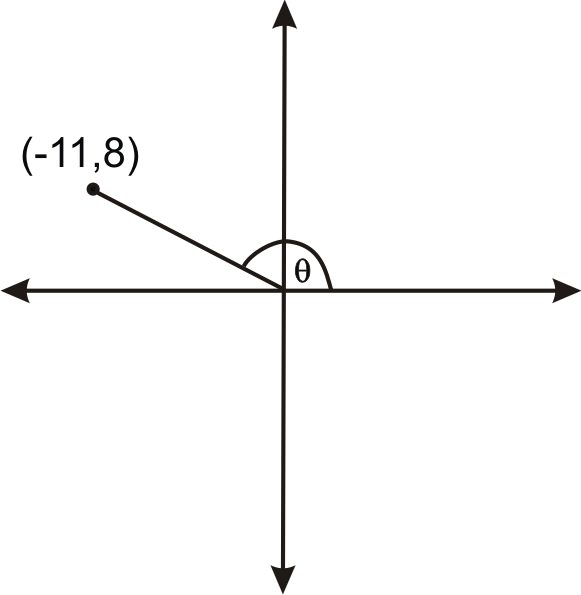
  ::角的三角数值 tan 409 是已知的, 但不是角度 。 在此情况下, 三角数函数的反面必须用于确定角的测量值 。 正切函数的反反面读作“ 切反 ” , 也称为 弧切关系 。 余弦函数的反面读作“ cosine 反面 ” , 也称为 arccosine 关系 。 正弦函数的反面读作“ 反面 ” , 也称为 arcsine 关系 。

  播放段落

  2. Find the angle, $\begin{array}{r}\theta \end{array}$ , in standard position.
  ::2. 在标准位置上找到角度 。

  

  播放段落

  The $\begin{array}{r}\tan \theta =\frac{y}{x}\end{array}$ or, in this case, $\begin{array}{r}\tan \theta =\frac{8}{-11}\end{array}$ . Using the inverse tangent, you get $\begin{array}{r}{\tan }^{-1}-\frac{8}{11}=-{36.03}^{\circ }\end{array}$ . This means that the reference angle is $\begin{array}{r}{36.03}^{\circ }\end{array}$ . This value of $\begin{array}{r}{36.03}^{\circ }\end{array}$ is the angle you also see if you move counterclockwise from the -x axis. To find the corresponding angle in the second quadrant (which is the same as though you started at the +x axis and moved counterclockwise), subtract $\begin{array}{r}{36.03}^{\circ }\end{array}$ from $\begin{array}{r}{180}^{\circ }\end{array}$ , yielding $\begin{array}{r}{143.97}^{\circ }\end{array}$ .
  ::tanyx , 或在此情况下为 tan_ 8- 11。 使用反正正切, 您可以得到 tan- 1 - 811 36. 03\\\ 。 这意味着引用角度为 36. 03\\ 。 这36. 03\ 的值也是您从 -x 轴逆时针移动的角度。 要在第二个象限中找到相应的角度( 与您从 +x 轴开始, 逆向移动相同) , 从 180\ 中减去 36.03\ , 产生 143.97\ 。

  播放段落

  3. Recall that inverse trigonometric functions are also used to find the angle of depression or elevation.
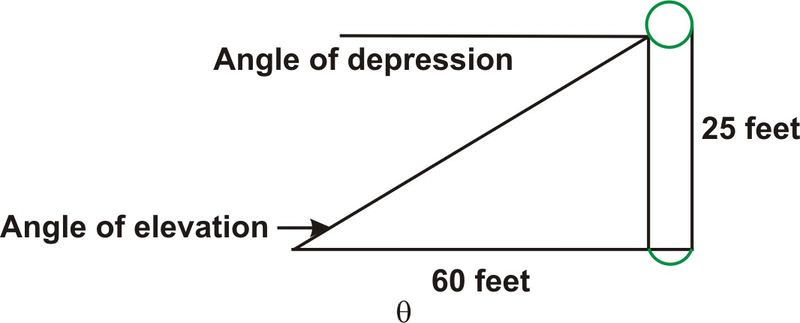
  ::3. 回顾逆三角函数也被用于寻找压抑或高角。

  播放段落

  A new outdoor skating rink has just been installed outside a local community center. A light is mounted on a pole 25 feet above the ground. The light must be placed at an angle so that it will illuminate the end of the skating rink. If the end of the rink is 60 feet from the pole, at what angle of depression should the light be installed?
  ::刚刚在本地社区中心外安装了一个新的户外滑冰场。 在地面上25英尺处的杆上安装了灯光。 光线必须放在一个角度上, 以便它能够照亮滑冰场的尽头。 如果冰场的尽头离杆60英尺, 那么光线应该安装到什么抑郁角度上?

  

  播放段落

   In this diagram, the angle of depression, which is located outside of the triangle, is not known. Recall, the angle of depression equals the angle of elevation. For the angle of elevation, the pole where the light is located is the opposite and is 25 feet high. The length of the rink is the adjacent side and is 60 feet in length. To calculate the measure of the angle of elevation the trigonometric ratio for tangent can be applied.
  ::在此图中, 位于三角形外的抑郁角未知。 回想时, 抑郁角等于高度角。 对于高角, 光点所在的极是相反的, 高25英尺。 斜点的长度是相邻边的, 长60英尺。 要计算高角的度量, 可以应用对正切度的三角测量比 。

  播放段落

  $$\begin{array}{r}\tan \theta =\frac{25}{60}\\ \tan \theta =0.4166\\ {\tan }^{-1}(\tan \theta )={\tan }^{-1}(0.4166)\\ \theta ={22.6}^{\circ }\end{array}$$

  
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

  播放段落

  The angle of depression at which the light must be placed to light the rink is $\begin{array}{r}{22.6}^{\circ }\end{array}$
  ::将灯光点亮的压抑角度是22.6

  播放段落

  Examples
  ::实例

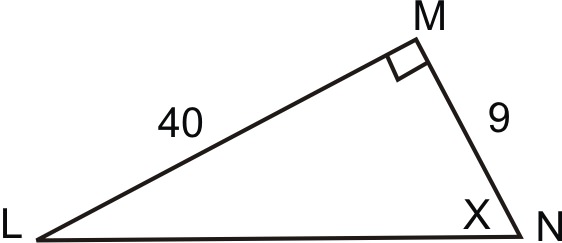
  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem on inverse trig functions. 
  ::早些时候,你遇到一个反三角函数的问题。

  播放段落

  Since you now know about inverse trigonometric ratios, you know that you can apply the inverse of a trig function to help solve this problem. For example, it is straightforward to apply the tangent function:
  ::既然你现在知道逆三角比,你就可以应用三角函数的反函数来帮助解决这个问题。例如,直接应用正切函数可以直截了当:

  播放段落

  $$\begin{array}{r}\tan \theta =\frac{35}{12}\\ \theta ={\tan }^{-1}\frac{35}{12}\\ \theta ={71.08}^{\circ }\end{array}$$

  
  ::35121351271.08

  播放段落

  You can find the other angle the in a similar manner, this time using the sine function:
  ::您可以以类似的方式找到另一个角度, 这次使用正弦函数 :

  播放段落

  $$\begin{array}{r}\sin \theta =\frac{12}{37}\\ \theta ={\sin }^{-1}\frac{12}{37}\\ \theta ={18.92}^{\circ }\end{array}$$

  
  ::1237 18.92 \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Example 2
  ::例2

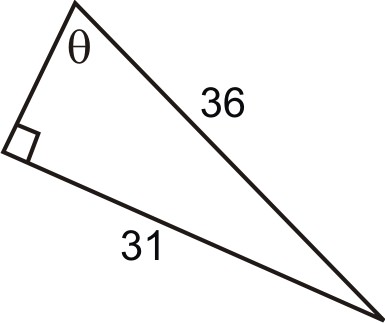
  播放段落

  Find the value of the missing angle.
  ::查找丢失角度的值 。

  

  播放段落

  $\begin{array}{r}\cos \theta =\frac{12}{17}\to {\cos }^{-1}\frac{12}{17}={45.1}^{\circ }\end{array}$
  :cos1217cos-11217=45.1)

  播放段落

  Example 3
  ::例3

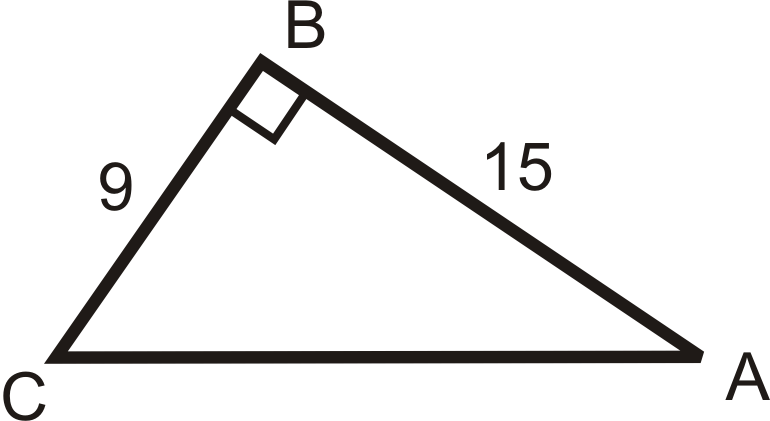
  播放段落

  Find the value of the missing angle.
  ::查找丢失角度的值 。

  

  播放段落

  $\begin{array}{r}\sin \theta =\frac{31}{36}\to {\sin }^{-1}\frac{31}{36}={59.44}^{\circ }\end{array}$
  ::-================================================================================================================================================= =====================================================================================================================================================

  播放段落

  Example 4
  ::例4

  播放段落

  What is the value of the angle with its terminal side passing through (-14, -23)?
  ::其终点边经过( 14, - 23) 的角度值是多少 ?

  播放段落

  This problem uses tangent inverse. $\begin{array}{r}\tan x=\frac{-23}{-14}\to x={\tan }^{-1}\frac{23}{14}={58.67}^{\circ }\end{array}$ (value graphing calculator will produce). However, this is the reference angle. Our angle is in the third quadrant because both the $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ values are negative. The angle is $\begin{array}{r}{180}^{\circ }+{58.67}^{\circ }={238.67}^{\circ }\end{array}$ .
  ::这个问题使用正切反方向 。 tanx23- 14x=tan- 12314=58. 67( 数值图形计算计算器将生成 ) 。 但是, 这是参考角度 。 我们的角度位于第三个象限, 因为 X 和 y 值都是负的 。 角度是 18058. 67\\ 238. 67 。

  播放段落

  Review
  ::回顾

  播放段落

  Find the measure of angle A in each triangle below.
  ::在下方每个三角形中查找角A的度量。

  1. 
  2. 
  3. 
  4. 
  5. 

  播放段落

  Use inverse tangent to find the value of the angle with its terminal side passing through each of the given points.
  ::使用反正切值查找角度的值, 其终端侧通过给定的每个点 。

  6. (-3,4)
  7. (12,13)
  8. (-4, -7)
  9. (5, -4)
  10. (-6, 10)
  11. (-3, -10)
  12. (6, 8)

  播放段落

  Use inverse trigonometry to solve each problem.
  ::使用逆三角测量法解决每个问题。

  播放段落
  13. A 30 foot building casts a 60 foot shadow. What is the angle the sun hits the building from the horizon?
      ::太阳从地平线进入大楼的角度是什么?
  播放段落
  14. Over 3 miles (horizontal), a road rises 100 feet (vertical). What is the angle of elevation?
      ::3英里以上(横向),一条公路上升100英尺(垂直)。高处的角是什么?
  播放段落
  15. An 80 foot building casts a 20 foot shadow. What is the angle the sun hits the building from the horizon?
      ::太阳从地平线到大楼的角度是什么?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。