课程： 12.5 反射 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节反思

折叠展开
反思
Reflections
::反思

A transformation is an operation that moves, flips, or otherwise changes a figure to create a new figure. A rigid transformation (also known as an isometry or congruence transformation ) is a transformation that does not change the size or shape of a figure.
::变换是一种移动、翻转或以其他方式改变数字以创建新图的操作。僵硬变换( 也称为等离线或相容变换) 是一种不会改变图的大小或形状的变换。

The rigid transformations are translations, reflections , and rotations . The new figure created by a transformation is called the image . The original figure is called the preimage . If the preimage is $\begin{align*}A\end{align*}$ , then the image would be $\begin{align*}A'\end{align*}$ , said “a prime.” If there is an image of $\begin{align*}A'\end{align*}$ , that would be labeled $\begin{align*}A''\end{align*}$ , said “a double prime.”
::硬质变换是翻译、反射和旋转。由变换创造的新数字被称为图像。原始数字被称为预映。如果预映为A,那么图像将是A , “ 黄金 ” 。如果有A 的图像,则标为A 的A , “双质 ” , 则表示“双质 ” 。

A reflection is a transformation that turns a figure into its mirror image by flipping it over a line . The line of reflection is the line that a figure is reflected over. If a point is on the line of reflection then the image is the same as the preimage. Images are always congruent to preimages.
::反射是一种转换,它通过翻翻一行将其图象转换成镜像。反射线是图象反射的线条。如果一个点在反射线上,则图像与预映像相同。图像总是与预映一致的。

While you can reflect over any line, some common lines of reflection have rules that are worth memorizing:
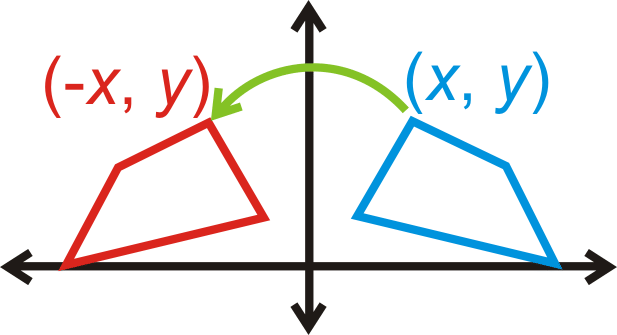
::虽然你可以反省任何一行, 但一些共同的反省路线有值得记住的规则:

Reflection over the $\begin{align*}y-\end{align*}$ axis: $\begin{align*}(x,y) \rightarrow (-x,y)\end{align*}$
::y- 轴反射 x,y) (- x,y) (- x,y)

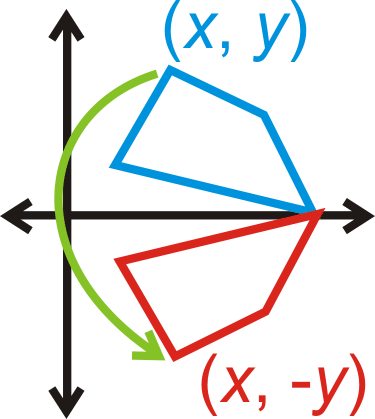
Reflection over the $\begin{align*}x-\end{align*}$ axis: $\begin{align*}(x,y) \rightarrow (x,-y)\end{align*}$
::x - 轴反射 x,y) (x,-y)

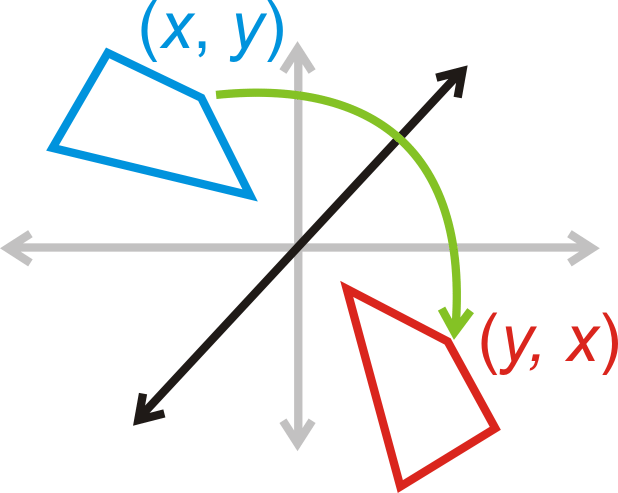
Reflection over $\begin{align*}y = x\end{align*}$ : $\begin{align*}(x,y)\rightarrow(y,x)\end{align*}$
::y=x 反射 y=xx,y) (y,x)

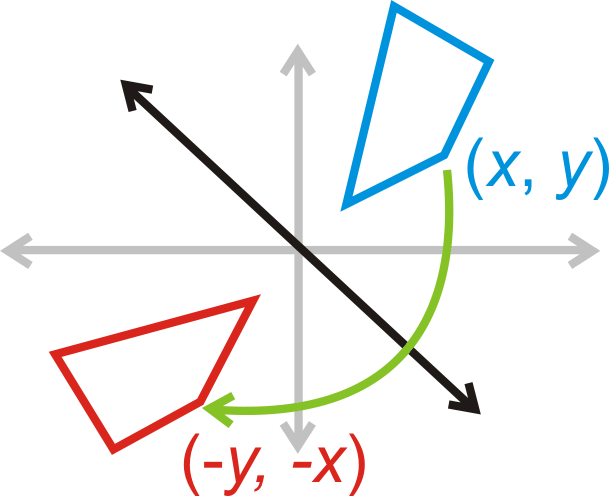
Reflection over $\begin{align*}y = -x\end{align*}$ : $\begin{align*}(x,y) \rightarrow (-y,-x)\end{align*}$
::yx的反射x,y)(-y,-x)

What if you were given the coordinates of a quadrilateral and you were asked to reflect that quadrilateral over the $\begin{align*}y-\end{align*}$ axis? What would its new coordinates be?
::如果你们获得四边形的座标,而你们被要求在Y-轴上反射四边形呢?它的新座标是什么?

Examples
::实例

Example 1
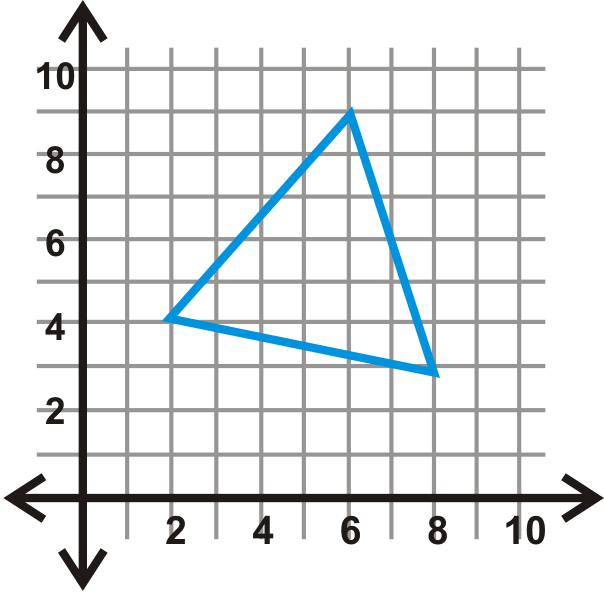
::例1

Reflect $\begin{align*}\triangle ABC\end{align*}$ over the $\begin{align*}y-\end{align*}$ axis. Find the coordinates of the image.
::在 y - 轴上反射 ABC。找到图像的坐标。

$\begin{align*}\triangle A'B'C'\end{align*}$ will be the same distance away from the $\begin{align*}y-\end{align*}$ axis as $\begin{align*}\triangle ABC\end{align*}$ , but on the other side. Hence, their $\begin{align*}x\end{align*}$ -coordinates will be opposite .
::与y-axis的距离与 QABC的距离相同, 但是在另一侧。因此, 它们的X坐标将相反。

$\begin{aligned} A (4, 3) \to A^{'} (- 4, 3) \\ B (7, - 1) \to B^{'} (- 7, - 1) \\ C (2, - 2) \to C^{'} (- 2, - 2) \end{aligned}$
$\begin{align*}& A(4,3) \rightarrow A'(-4,3)\\ & B(7,-1) \rightarrow B'(-7,-1)\\ & C(2,-2) \rightarrow C'(-2,-2)\end{align*}$
::A(4,3)A[(4,3)A[(4,4,3)B(7,-1)B[(7)-(1)B[(7)-(7)-(7)-(1)C(2)-(2)-(C)-(2)-(2)-(2))

Example 2
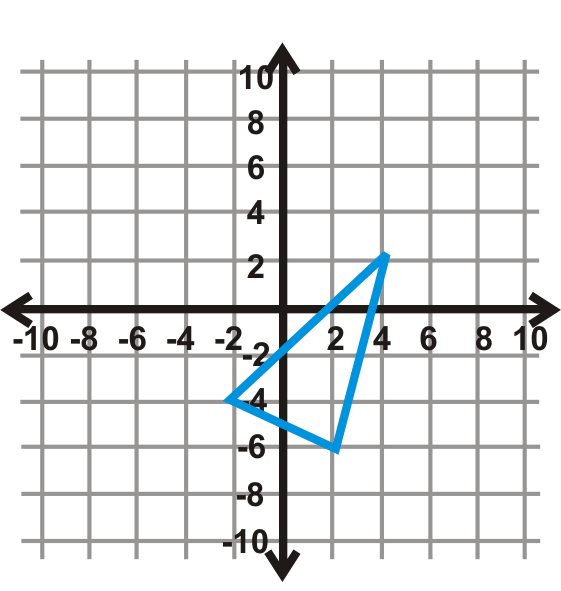
::例2

Reflect the letter $\begin{align*}``F''\end{align*}$ over the $\begin{align*}x-\end{align*}$ axis.
::在 x - 轴上反射字母 'F' 。

When reflecting the letter $\begin{align*}F\end{align*}$ over the $\begin{align*}x-\end{align*}$ axis, the $\begin{align*}y-\end{align*}$ coordinates will be the same distance away from the $\begin{align*}x-\end{align*}$ axis, but on the other side of the $\begin{align*}x-\end{align*}$ axis. Hence, their $\begin{align*}y\end{align*}$ -coordinates will be opposite.
::当反射 x - 轴的字母 F 时, y - 坐标将与 x - 轴的距离相同, 但位于 x - 轴的另外一边。因此, 它们的 Y 坐标将是相反的。

Example 3
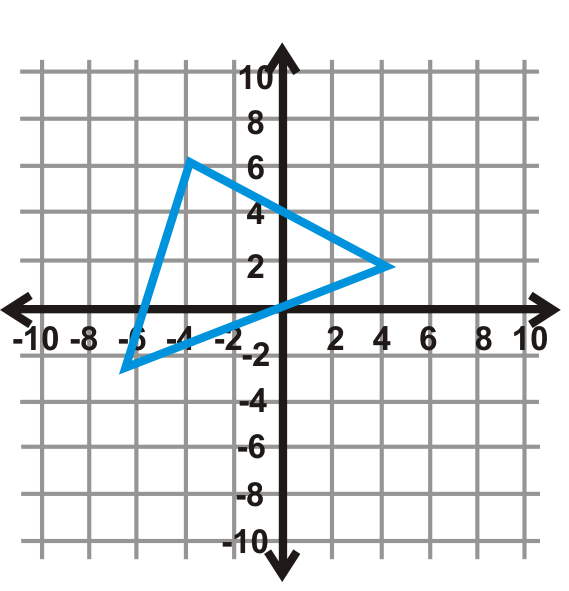
::例3

Reflect the triangle $\begin{align*}\triangle ABC\end{align*}$ with vertices $\begin{align*}A(4, 5), B(7, 1)\end{align*}$ and $\begin{align*}C(9, 6)\end{align*}$ over the line $\begin{align*}x = 5\end{align*}$ . Find the coordinates of $\begin{align*}A'\end{align*}$ , $\begin{align*}B'\end{align*}$ , and $\begin{align*}C'\end{align*}$ .
::反射横线x=5的A(4)5、B(7)、B(7)和C(9、6)三角形 ABC 。

The image’s vertices are the same distance away from $\begin{align*}x = 5\end{align*}$ as those of the preimage.
::图像的顶部距离 x=5 与预感的顶部距离相同。

$\begin{aligned} A (4, 5) \to A^{'} (6, 5) \\ B (7, 1) \to B^{'} (3, 1) \\ C (9, 6) \to C^{'} (1, 6) \end{aligned}$
$\begin{align*}& A(4,5) \rightarrow A'(6,5)\\ & B(7,1) \rightarrow B'(3,1)\\ & C(9,6) \rightarrow C'(1,6)\end{align*}$
::A(4,5,5)A*A[6,5,5,B(7,1,1)B*(3,3,1)C(9,6)C__C[1,6)

Example 4
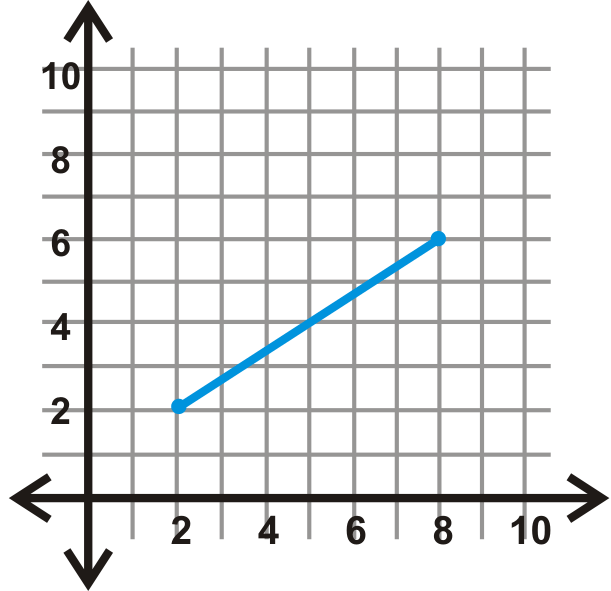
::例4

Reflect the line segment $\begin{align*}\overline{PQ}\end{align*}$ with endpoints $\begin{align*}P(-1, 5)\end{align*}$ and $\begin{align*}Q(7, 8)\end{align*}$ over the line $\begin{align*}y = 5\end{align*}$ .
::反射线段 PQ ,端点为 P(1,5) 和 Q(7,8) ,端点为 y= 5 。

$\begin{align*}P\end{align*}$ is on the line of reflection, which means $\begin{align*}P'\end{align*}$ has the same coordinates. $\begin{align*}Q'\end{align*}$ is the same distance away from $\begin{align*}y = 5\end{align*}$ , but on the other side.
::P在反射线上, 这意味着P有相同的坐标。 \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\在距离y=5,但在另一侧。

$\begin{aligned} P (- 1, 5) & \to P^{'} (- 1, 5) \\ Q (7, 8) & \to Q^{'} (7, 2) \end{aligned}$
$\begin{align*}P(-1,5) & \rightarrow P'(-1,5)\\ Q(7,8) & \rightarrow Q'(7,2)\end{align*}$
::P(1,1,5,5)PP(-1,5)Q(7,8)(7,2)

Example 5
::例5

A triangle $\begin{align*}\triangle LMN\end{align*}$ and its reflection, $\begin{align*}\triangle L'M'N'\end{align*}$ are below. What is the line of reflection?
::三角的LMN及其反射在下面。反射线是什么?

Looking at the graph, we see that the corresponding parts of the preimage and image intersect when $\begin{align*}y = 1\end{align*}$ . Therefore, this is the line of reflection.
::查看图时,我们看到预视和图像的相应部分在y=1时相互交叉。因此,这是反射线。

If the image does not intersect the preimage, find the midpoint between the preimage point and its image. This point is on the line of reflection.
::如果图像不交叉图像预映, 请在预映点与其图像之间找到中点。此点在反射线上。

Example 6
::例6

Reflect the trapezoid $\begin{align*}TRAP\end{align*}$ over the line $\begin{align*}y = -x\end{align*}$ .
::反射横线yx的陷阱图。

The purple line is $\begin{align*}y = -x\end{align*}$ . You can reflect the trapezoid over this line.
::紫色线是yx。你可以反射到这个线上的。

$\begin{aligned} T (2, 2) \to T^{'} (- 2, - 2) \\ R (4, 3) \to R^{'} (- 3, - 4) \\ A (5, 1) \to A^{'} (- 1, - 5) \\ P (1, - 1) \to P^{'} (1, - 1) \end{aligned}$
$\begin{align*}& T(2,2) \rightarrow T'(-2,-2)\\ & R(4,3) \rightarrow R'(-3,-4)\\ & A(5,1) \rightarrow A'(-1,-5)\\ & P(1,-1) \rightarrow P'(1,-1)\end{align*}$
::T(2,2,2)T(-2,2,2)R(4,3)R[3,4)A(5,1)A[A]A[(-1,1,5)P(1,1)P(1,1)-1)

Review
::回顾

If (5, 3) is reflected over the $\begin{align*}y-\end{align*}$ axis, what is the image?
::如果(5,3)在y-轴上反射,图像是什么?

If (5, 3) is reflected over the $\begin{align*}x-\end{align*}$ axis, what is the image?
::如果 X - 轴反射到( 5, 3) , 图像是什么 ?

If (5, 3) is reflected over $\begin{align*}y = x\end{align*}$ , what is the image?
::如果(5,3)在y=x上方反射,图像是什么?

If (5, 3) is reflected over $\begin{align*}y = -x\end{align*}$ , what is the image?
::如果(5,3)在yx上方反射,图像是什么?

Plot the four images. What shape do they make? Be specific.
::绘制四张图像。它们的形状是什么? 具体化。

Which letter is a reflection over a vertical line of the letter $\begin{align*}``b''\end{align*}$ ?
::哪个字母反射在字母“b”的垂直线上?

Which letter is a reflection over a horizontal line of the letter $\begin{align*}``b''\end{align*}$ ?
::哪个字母反射在字母“b”的横向线上?

Find the coordinates of the image reflected over the given line.
::查找在给定线上反射的图像坐标。

$\begin{align*}y-\end{align*}$ axis
::y - 轴

$\begin{align*}x-\end{align*}$ axis
::x - 轴

$\begin{align*}y = 3\end{align*}$
::y=3 y=3

$\begin{align*}x = -1\end{align*}$
::x1

$\begin{align*}x-\end{align*}$ axis
::x - 轴

$\begin{align*}y-\end{align*}$ axis
::y - 轴

$\begin{align*}y = x\end{align*}$
::y=x y=x

$\begin{align*}y = -x\end{align*}$
::yx

$\begin{align*}x = 2\end{align*}$
::x=2x=2

$\begin{align*}y = -4\end{align*}$
::y 4

$\begin{align*}y = -x\end{align*}$
::yx

$\begin{align*}y = x\end{align*}$
::y=x y=x

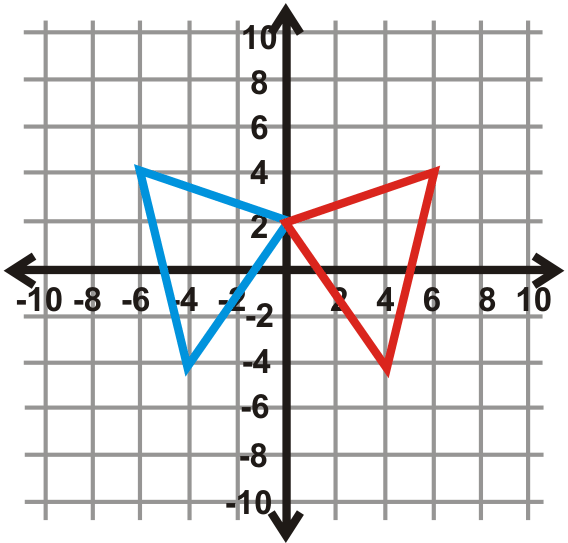
Find the line of reflection the blue triangle (preimage) and the red triangle (image).
::查找反射线蓝色三角形(预视)和红色三角形(图像) 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

反思

Reflections ::反思

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Reflections
::反思

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)