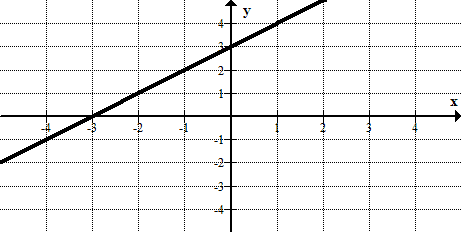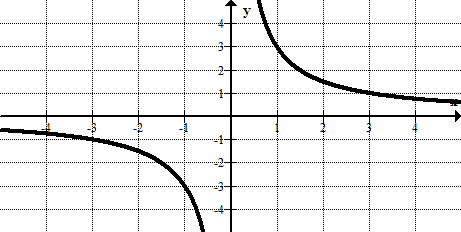Course: 4.4 地图绘制的逆数

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 映射逆向

Collapse Expand
映射逆向
Your instructor gives you a function, $\begin{aligned} f (x) = (x - 1)^{2} + 3 \end{aligned}$ , where $\begin{aligned} x \geq 1 \end{aligned}$ , and asks you to find the inverse. You are all set to start manipulating the equation, when your Instructor specifies that you should find the inverse by graphing instead of by algebraic manipulation.
::您的教官给了您一个函数 f( x) =( (x- 1) 2+ 3) , 其位置为 x+1, 并要求您找到反方向。当您的教官指定您应该通过图形而不是代数操控来查找反方向时, 您将全部设置为开始操控方程。

Are you able to do this?
::你能做到吗?

Finding the Inverse by Mapping
::通过绘图查找反向

Determining an inverse function algebraically can be both involved and difficult, so it is useful to know how to map $\begin{aligned} f \end{aligned}$ to $\begin{aligned} f^{- 1} \end{aligned}$ .
::确定反函数代数既可能涉及,也可能很困难,因此了解如何绘制f至f-1的图是有用的。

The graph of $\begin{aligned} f \end{aligned}$ can be used to produce the graph of $\begin{aligned} f^{- 1} \end{aligned}$ by applying the inverse reflection principle:
::f 的图解可用于通过应用反向反向反射原则来生成 f-1 的图解:

The points $\begin{aligned} (a, b) \end{aligned}$ and $\begin{aligned} (b, a) \end{aligned}$ in the coordinate plane are symmetric with respect to the line $\begin{aligned} y = x \end{aligned}$ .
::坐标平面上的点(a、b)和(b、a)与y=x线对称。

The points $\begin{aligned} (a, b) \end{aligned}$ and $\begin{aligned} (b, a) \end{aligned}$ are reflections of each other across the line $\begin{aligned} y = x \end{aligned}$ .
::点(a、b)和点(b、a)是横跨y=x线的反射。

Finding the Inverse of a Function
::查找函数的反向

1. Find the inverse of $\begin{aligned} f (x) = \frac{1}{x - 5} \end{aligned}$ by mapping.
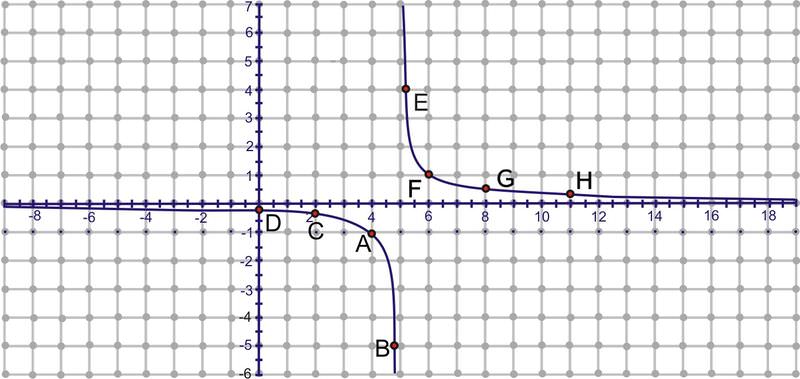
::1. 通过绘图查找 f(x)=1x-5的反差。

From the last section, we know that the inverse of this function is $\begin{aligned} y = \frac{5 x + 1}{x} \end{aligned}$ . To find the inverse by mapping, pick several points on $\begin{aligned} f (x) \end{aligned}$ , reflect them using the reflection principle and plot. Note: The coordinates of some of the points are rounded.
::从上一节中,我们知道此函数的反向值是 y= 5x+1x。要通过绘图找到反向值,请在 f(x) 上选择几个点,用反射原则和绘图来反映这些点。注意:一些点的坐标是四舍五入的。

A: (4, -1)
::A: (4,-1)

B: (4.8, -5)
::B4.8、5)

C: (2, -0.3)
::C2,-0.3)

D: (0, -0.2)
::D: (0,-0.2)

E: (5.3, 3.3)
::英5.3、3.3)

F: (6, 1)
::法6,1)

G: (8, 0.3)
::G: (8,0.3)

H: (11, 0.2)
::H11,0.2)

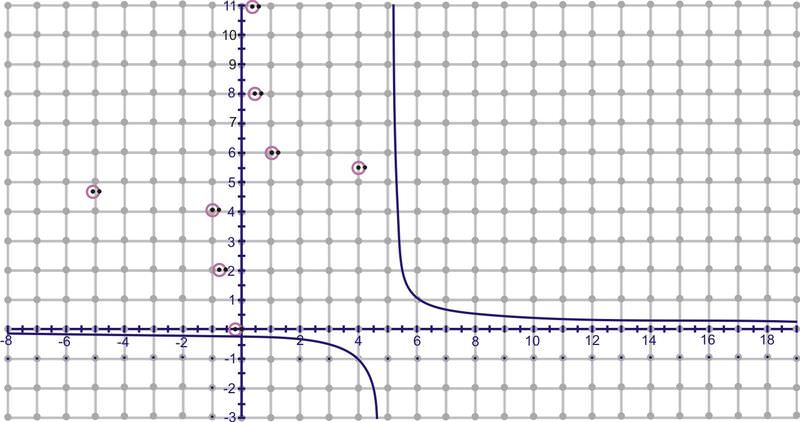
Now, take these eight points, switch the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ and plot $\begin{aligned} (y, x) \end{aligned}$ . Connect them to make the inverse function.
::现在,拿这八个点, 切换 x 和 Y , 绘制( y, x) 。连接它们来产生反函数。

$\begin{aligned} A^{- 1} : (- 1, 4) \end{aligned}$
::A-1:1-1,4)

$\begin{aligned} B^{- 1} : (- 5, 4.8) \end{aligned}$
::B-1-5,4.8)

$\begin{aligned} C^{- 1} : (- 0.3, 2) \end{aligned}$
::C-1-0.3,2)

$\begin{aligned} D^{- 1} : (- 0.2, 0) \end{aligned}$
::D-1-0.2.0)

$\begin{aligned} E^{- 1} : (3.3, 5.3) \end{aligned}$
::E-13.3,5.3)

$\begin{aligned} F^{- 1} : (1, 6) \end{aligned}$
::F-1:1(1,6)

$\begin{aligned} G^{- 1} : (0.3, 8) \end{aligned}$
::G-1:1(0.3.8)

$\begin{aligned} H^{- 1} : (0.2, 11) \end{aligned}$
::H-1:1(0.2.11)

Not all functions have inverses that are one-to-one. However, the inverse can be modified to a one-to-one function if a “restricted domain” is applied to the inverse function.
::并非所有函数都有一对一的反函数。但是,如果“ 限制域” 应用于反函数, 反函数可以修改为一对一的函数。

2. Find the inverse of $\begin{aligned} f (x) = x^{2} - 4 \end{aligned}$ .
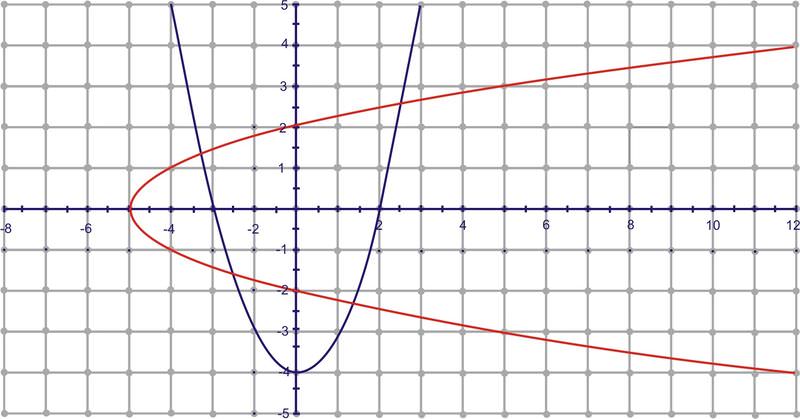
::2. 查找 f(x) =x2-4的反义值。

Let’s use the graphic approach for this one. The function is graphed in blue and its inverse is red.
::让我们为此使用图形处理法。函数以蓝色图解, 反面图解为红色。

Clearly, the inverse relation is not a function because it does not pass the vertical line test. This is because all parabolas fail the horizontal line test . To “make” the inverse a function, we restrict the domain of the original function. For parabolas, this is fairly simple. To find the inverse of this function algebraically, we get $\begin{aligned} f^{- 1} (x) = \sqrt{x + 4} \end{aligned}$ . Technically, however, the inverse is $\begin{aligned} \pm \sqrt{x + 4} \end{aligned}$ because the square root of any number could be positive or negative. So, the inverse of $\begin{aligned} f (x) = x^{2} - 4 \end{aligned}$ is both parts of the square root equation, $\begin{aligned} \sqrt{x + 4} \end{aligned}$ and $\begin{aligned} - \sqrt{x + 4} \end{aligned}$ . $\begin{aligned} \sqrt{x + 4} \end{aligned}$ will yield the top portion of the horizontal parabola and $\begin{aligned} - \sqrt{x + 4} \end{aligned}$ will yield the bottom half. Be careful, because if you just graph $\begin{aligned} f^{- 1} (x) = \sqrt{x + 4} \end{aligned}$ in your graphing calculator, it will only graph the top portion of the inverse.
::显然,反关系不是一个函数, 因为它没有通过垂直线测试。这是因为所有 parabolas 都失败了水平线测试。对于“ make” 函数的反向, 我们限制原始函数的域。对于 parabolas 来说, 这相当简单。要找到此函数的反向代数, 我们得到 f - 1 (x) =x+4 。然而, 从技术上讲, 逆差为 +4 , 因为任何数字的平根都可能是正的或负的。因此, f( x) =x2 - 4 的反方向是正方根方形方形的两部分, x+4 和 +- x+4. x+4 的反方向将产生水平参数的顶部部分, 和 +4 将产生底部半。注意, 因为如果您在图形化计算器中只绘制 f-1 (x) = x+4, 它只会只绘制反面的顶部。

This technique of sectioning the inverse is applied to finding the inverse of trigonometric functions because it is periodic.
::这种分解反向技术用于发现三角函数的反向,因为三角函数是周期性的。

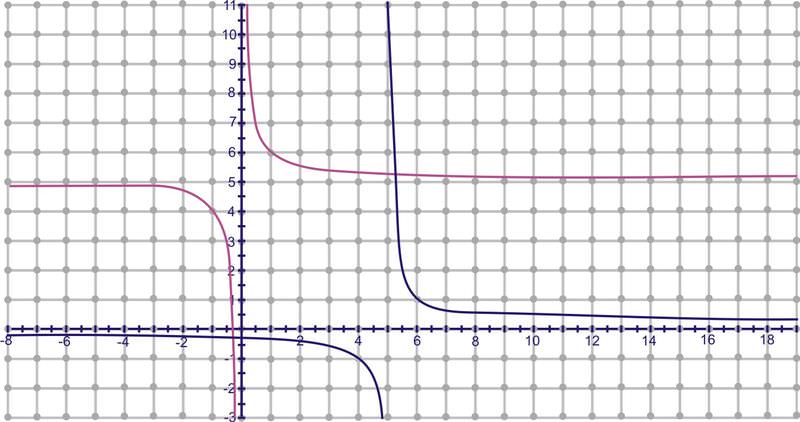
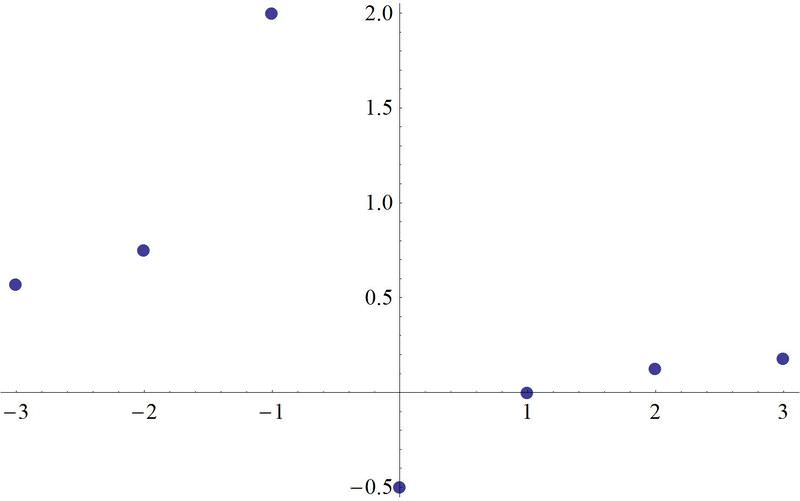
3. Find the inverse of $\begin{aligned} f (x) = \frac{x - 1}{3 x + 2} \end{aligned}$ mapping.
::3. 查找 f(x) =x- 13x+2 映射的反方向。

To find the inverse by mapping, pick several points on $\begin{aligned} f (x) \end{aligned}$ , reflect them using the reflection principle and plot. Note: The coordinates of some of the points are rounded.
::为了通过绘图找到相反的点,在 f(x) 上选择几个点, 使用反射原则和绘图来反映这些点。注意: 一些点的坐标是四舍五入的。

A: (0, -.5)
::A0)-(5)

B: (-1, 2)
::B-1,2)

C: (1, 0)
::C1,0)

D: (-2, .75)
::D-2, .75)

E: (2, .125)
::英2,125)

F: (-3, .57)
::F-3,.57)

G: (3, .18)
::G3,.18)

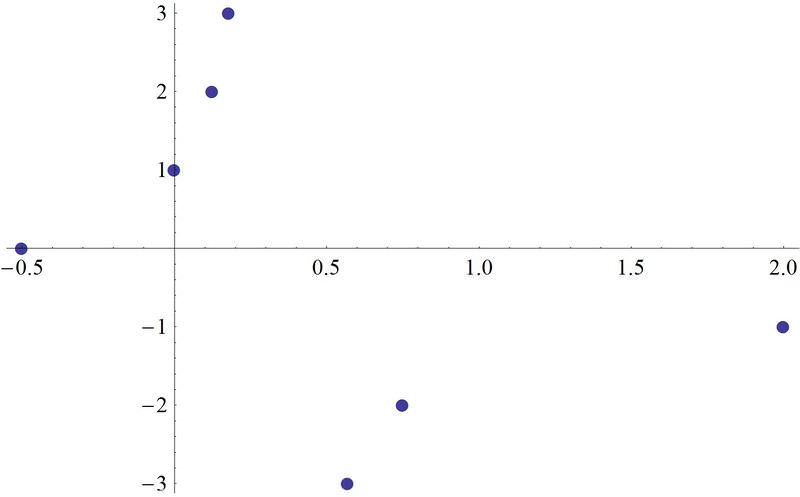
Now, take these seven points, switch the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ and plot $\begin{aligned} (y, x) \end{aligned}$ . Connect them to make the inverse function.
::现在, 取这七个点, 切换 x 和 Y , 绘制( y, x) 。连接它们来产生反函数。

$\begin{aligned} A^{- 1} : (- .5, 0) \end{aligned}$
::A-1-5.0)

$\begin{aligned} B^{- 1} : (2, - 1) \end{aligned}$
::B-1:1(2,-1)

$\begin{aligned} C^{- 1} : (0, 1) \end{aligned}$
::C-1:1(0,1)

$\begin{aligned} D^{- 1} : (.75, - 2) \end{aligned}$
::D-1-1.75,-2)

$\begin{aligned} E^{- 1} : (.125, 2) \end{aligned}$
::E-11125,2)

$\begin{aligned} F^{- 1} : (.57, - 3) \end{aligned}$
::F-1:1.57,-3-3)

$\begin{aligned} G^{- 1} : (.18, 3) \end{aligned}$
::G-118,3)

Not all functions have inverses that are one-to-one. However, the inverse can be modified to a one-to-one function if a “restricted domain” is applied to the inverse function.
::并非所有函数都有一对一的反函数。但是,如果“ 限制域” 应用于反函数, 反函数可以修改为一对一的函数。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the inverse of a function.
::早些时候,有人要求你找出函数的反面。

The original equation is $\begin{aligned} f (x) = (x - 1)^{2} + 3 \end{aligned}$ .
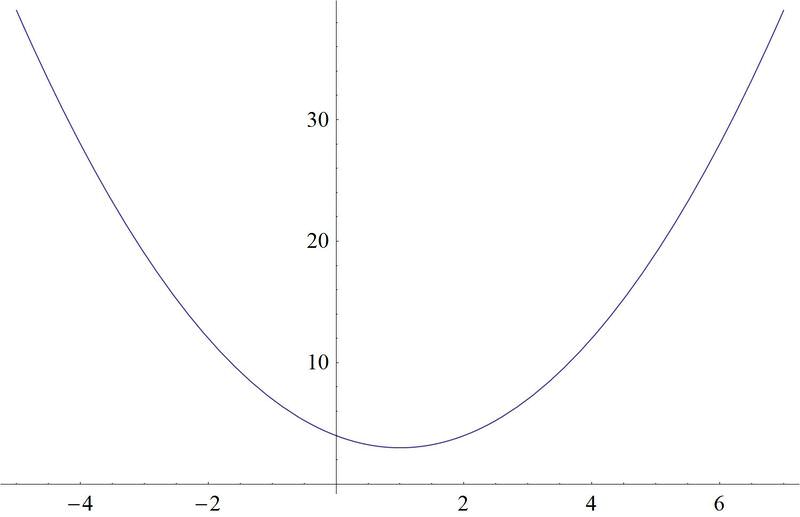
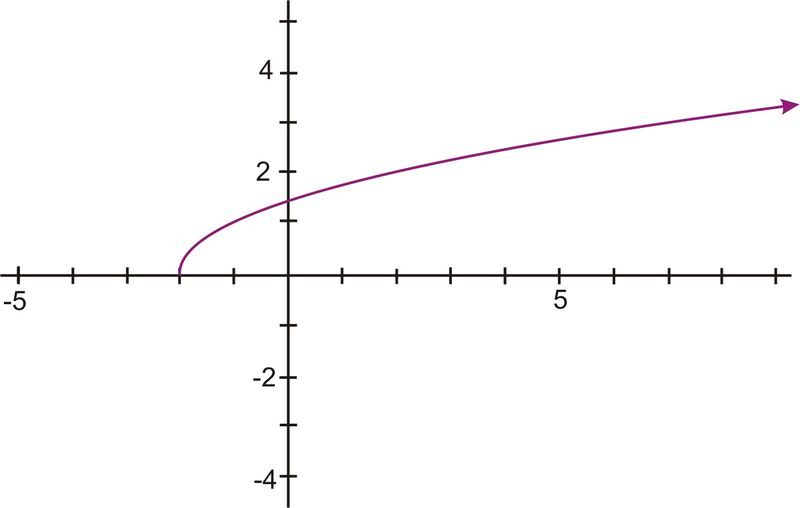
::原始方程式是 f(x) =(x- 1) 2+3 。

Here is a plot of the function:
::以下是函数的图示 :

Notice that the domain of the function under examination has to be restricted to 1 or greater, so that the function will pass the horizontal line test. Some points that are on this graph are:
::注意正在检查的函数域必须限制在 1 或 1 以上, 以便函数通过水平线测试。此图上的一些点是 :

A: (1, 3)
::A1,3)

B: (2, 4)
::B2,4)

C: (3, 7)
::C3,7)

To map the inverse function, first take each point and switch the "x" and "y" values:
::要绘制反向函数, 请先选择每个点, 然后切换“ x” 和“ Y” 值 :

$\begin{aligned} A^{- 1} : (3, 1) \end{aligned}$
::A-11: (3,1)

$\begin{aligned} B^{- 1} : (4, 2) \end{aligned}$
::B-11: (4,2)

$\begin{aligned} C^{- 1} : (7, 3) \end{aligned}$
::C-117,3)

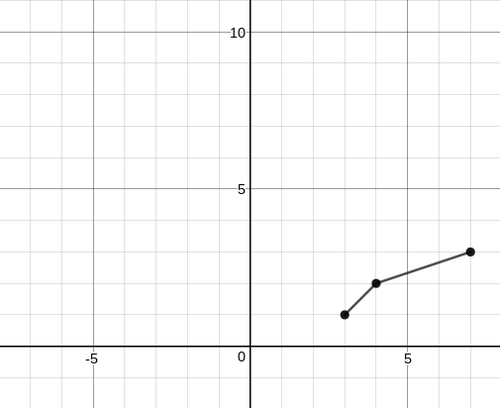
Then connect these dots, and you can see the graph of the inverse function. The inverse function graph looks like this:
::然后将这些点连接, 您可以看到反向函数的图形。反向函数图形看起来像这样 :

In this case, the range of the function has to be restricted to be 1 or greater, so that the inverse function will pass the vertical line test.
::在这种情况下,函数的范围必须限制在1或以上,以便反函数通过垂直线测试。

Example 2
::例2

Study the following graph and answer these questions:
::研究下图并回答这些问题:

Is the graphed relation a function?
::图表显示的关系是否函数?

Does the relation have an inverse that is a function?
::关系中是否有相反的函数呢?

The graph represents a one-to-one function. It passes both a vertical and a horizontal line test. The inverse would be a function.
::图形代表一对一的函数。它通过垂直和水平线测试。反之则是一个函数。

Example 3
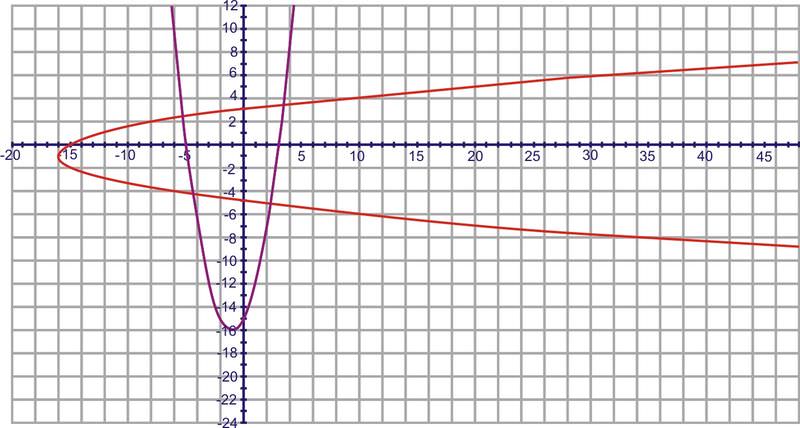
::例3

Find the inverse of $\begin{aligned} f (x) = x^{2} + 2 x - 15 \end{aligned}$ using the mapping principle.
::使用映射原理查找 f( x) =x2+2x- 15 的反义。

By selecting 4-5 points and switching the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values, you will get the red graph below.
::通过选择 4 - 5 点并切换 x 和 y 值,您将得到下面的红图。

Example 4
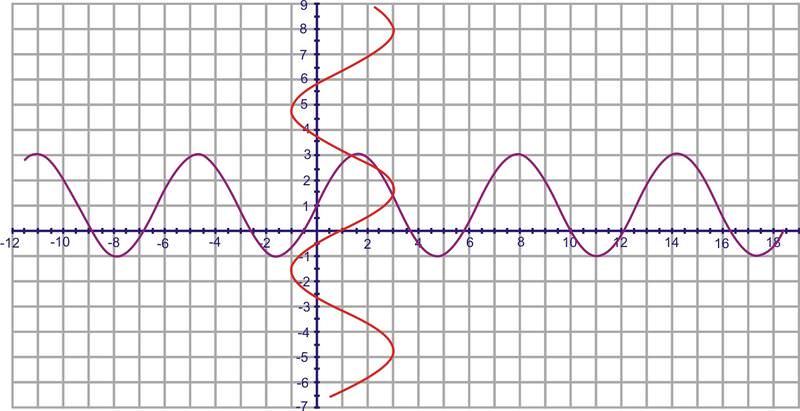
::例4

Find the inverse of $\begin{aligned} y = 1 + 2 \sin x \end{aligned}$ using the mapping principle.
::使用映射原理查找 y=1+2sinx 的反义。

By selecting 4-5 points and switching the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values, you will get the red graph below.
::通过选择 4 - 5 点并切换 x 和 y 值,您将得到下面的红图。

Review
::回顾

For each of the following graphs answer these questions:
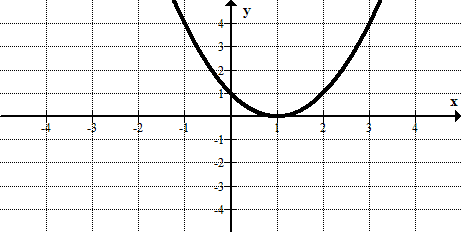
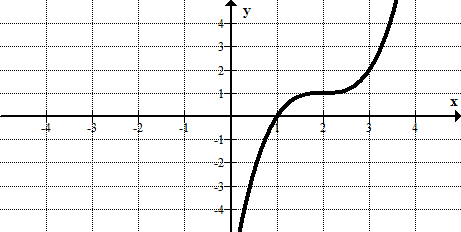
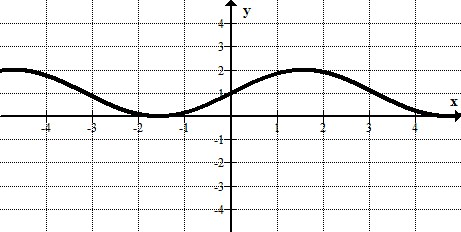
::以下每一图表回答这些问题:

(a) Is the graphed relation a function?
:a) 图示关系是否函数?

(b) Does the relation have an inverse that is a function?
:b) 这种关系是否有一种倒数函数?

Find the inverse of each function using the mapping principle.
::使用映射原则查找每个函数的反向。

$\begin{aligned} y = x^{2} + x - 2 \end{aligned}$
::y=x2+x-2 y=x2+x-2

$\begin{aligned} y = x^{3} \end{aligned}$
::y=x3 y=x3

$\begin{aligned} y = \sin (x - \frac{π}{2}) \end{aligned}$
::y=sin(x2)

$\begin{aligned} y = \cos (2 x) \end{aligned}$
::y=cos( 2x)

$\begin{aligned} y = \frac{1}{x} \end{aligned}$
::y=1x y=1x

$\begin{aligned} y = x^{2} - 9 \end{aligned}$
::y=x2 - 9

$\begin{aligned} y = - 2 + \sin (\frac{1}{2} x) \end{aligned}$
::y2+sin( 12x)

What type of points will be in the same place in both a function and its inverse?
::函数及其反函数的同一位置将显示哪类点 ?

When you graph a function and its inverse on the same set of axes, where is the line of reflection? Why?
::当您在同一组轴上绘制一个函数及其反向时,反射线在哪里?为什么?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

映射逆向

Finding the Inverse by Mapping ::通过绘图查找反向

Finding the Inverse of a Function ::查找函数的反向

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Finding the Inverse by Mapping
::通过绘图查找反向

Finding the Inverse of a Function
::查找函数的反向

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)