12.6 变革的构成

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节变革的构成

  折叠 展开

  变革的构成

  播放段落

  Transformations Summary
  ::转换概要

  播放段落

  A transformation is an operation that moves, flips, or otherwise changes a figure to create a new figure. A rigid transformation (also known as an isometry or congruence transformation ) is a transformation that does not change the size or shape of a figure. The new figure created by a transformation is called the image . The original figure is called the preimage .
  ::变换是一种移动、翻转或其他方式改变数字以创建新图的操作。 僵硬变换( 也称为等离线或相容变换) 是一种不会改变图的大小或形状的变换。 变换产生的新图被称为图像。 原图称为预视图。

  播放段落

  There are three rigid transformations: translations, rotations and reflections . A translation is a transformation that moves every point in a figure the same distance in the same direction. A rotation is a transformation where a figure is turned around a fixed point to create an image. A reflection is a transformation that turns a figure into its mirror image by flipping it over a line .
  ::有三种僵硬的转换:翻译、旋转和反射。翻译是一个转换,将数字中的每个点都移动在同一方向。一个旋转是一个转换,将数字围绕固定点转换,以创建图像。一个反射是一个转换,通过将图翻到一行,将图转换成镜像图像。

  播放段落

  Composition of Transformations
  ::变革的构成

  播放段落

  A composition (of transformations) is when more than one transformation is performed on a figure. Compositions can always be written as one rule. You can compose any transformations, but here are some of the most common compositions:
  ::组合( 变换) 是指在图形上进行多个变换时。 组合总是可以作为一条规则写入。 您可以组成任何变换, 但这里有一些最常见的组成 :

  播放段落
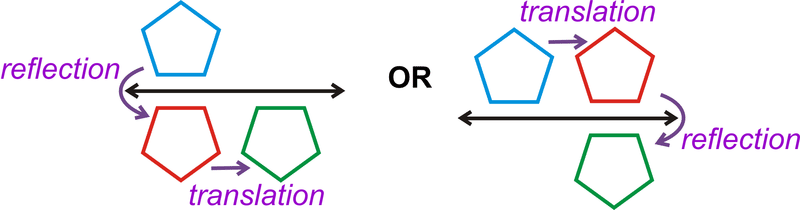
  1. A glide reflection is a composition of a reflection and a translation. The translation is in a direction parallel to the line of reflection.
     ::滑翔反射是反射和翻译的构成,翻译的方向与反射线平行。

  

  播放段落
  2. The composition of two reflections over parallel lines that are $\begin{array}{r}h\end{array}$ units apart is the same as a translation of $\begin{array}{r}2h\end{array}$ units ( Reflections over Parallel Lines Theorem ).
     ::平行线上两个反射面的构成为 h 个单位,与 2 个单位的翻译相同(平行线理论的反射)。

  

  播放段落
  3. If you compose two reflections over each axis, then the final image is a rotation of $\begin{array}{r}{180}^{\circ }\end{array}$ around the origin of the original ( Reflection over the Axes Theorem ).
     ::如果您在每一个轴上进行两个反射, 那么最后的图像将旋转 180\\\\ 围绕原始的起源( 对轴定理的反射) 。

  

  播放段落
  4. A composition of two reflections over lines that intersect at $\begin{array}{r}{x}^{\circ }\end{array}$ is the same as a rotation of $\begin{array}{r}2x^{\circ }\end{array}$ . The center of rotation is the point of intersection of the two lines of reflection ( Reflection over Intersecting Lines Theorem ).
     ::在 x\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  

  播放段落

  What if you were given the coordinates of a quadrilateral and you were asked to reflect the quadrilateral and then translate it? What would its new coordinates be?
  ::如果你们获得四边形的坐标,然后被要求反映四边形,然后翻译它呢?它的新坐标是什么?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

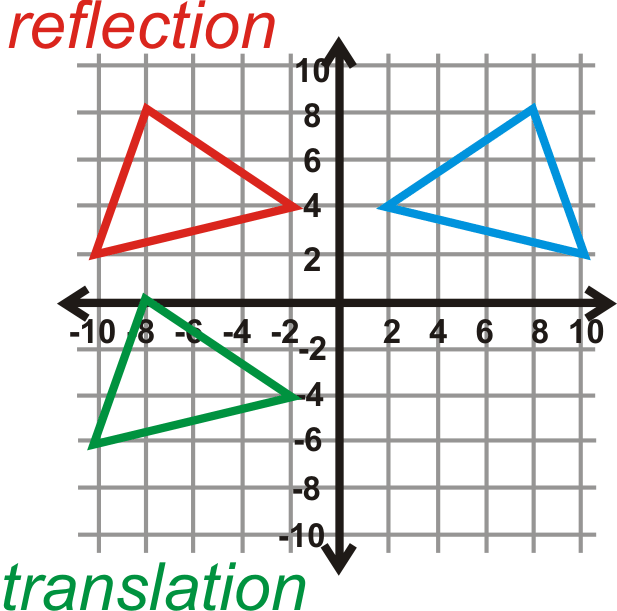
  Reflect $\begin{array}{r}\mathrm{△}ABC\end{array}$ over the $\begin{array}{r}y-\end{array}$ axis and then translate the image 8 units down.
  ::在 y - 轴上反射 ABC, 然后将图像 8 单位翻译下来 。

  

  播放段落

  The green image to the left  is the final answer.
  ::左边的绿色图像是最后答案。

  

  播放段落

  $$\begin{array}{rl}A(8,8)& \to A^{″}(-8,0)\\ B(2,4)& \to B^{″}(-2,-4)\\ C(10,2)& \to C^{″}(-10,-6)\end{array}$$

  
  :8,8)A(-8,0)B(2,4)B(-2,4)B(-2,4)C(10,2)C(-10,-6)

  播放段落

  Example 2
  ::例2

  播放段落

  Write a single rule for $\begin{array}{r}\mathrm{△}ABC\end{array}$ to $\begin{array}{r}\mathrm{△}{A}^{″}{B}^{″}{C}^{″}\end{array}$ from Example 1.
  ::将“ ABC” 的单一规则写成“ 例1” 中的“A” B” C” 。

  播放段落

  Looking at the coordinates of $\begin{array}{r}A\end{array}$ to $\begin{array}{r}{A}^{″}\end{array}$ , the $\begin{array}{r}x-\end{array}$ value is the opposite sign and the $\begin{array}{r}y-\end{array}$ value is $\begin{array}{r}y-8\end{array}$ . Therefore the rule would be $\begin{array}{r}(x,y)\to (-x,y-8)\end{array}$ .
  ::从A到A的坐标看,x值是相反的符号,y值是y-8。 因此,规则是(x,y)%(-x,y-8)。

  播放段落

  Example 3
  ::例3

  播放段落

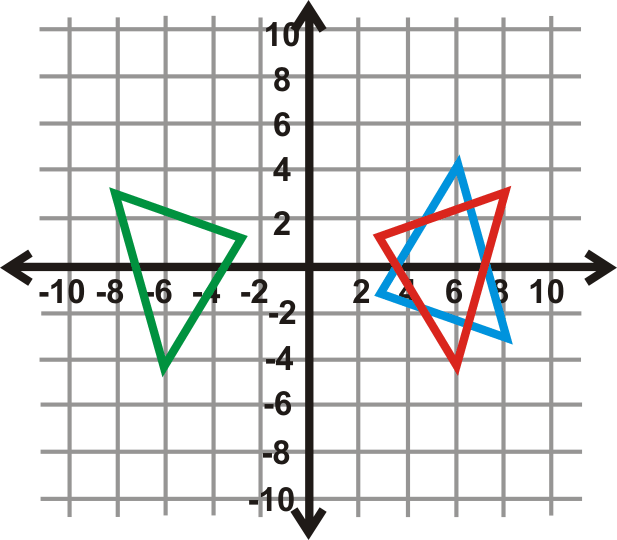
  Reflect $\begin{array}{r}\mathrm{△}ABC\end{array}$ over $\begin{array}{r}y=3\end{array}$ and then reflect the image over $\begin{array}{r}y=-5\end{array}$ .
  ::在 y= 3 上反射 ABC, 然后在 y 5 上映图像 。

  

  播放段落

  Order matters, so you would reflect over $\begin{array}{r}y=3\end{array}$ first, (red triangle) then reflect it over $\begin{array}{r}y=-5\end{array}$ (green triangle).
  ::顺序事项, 所以您会首先反射 Y= 3, (红色三角形) 然后反射 y= 5( 绿色三角形) 。

  

  播放段落

  Example 4
  ::例4

  播放段落

  A square is reflected over two lines that intersect at a $\begin{array}{r}{79}^{\circ }\end{array}$ angle . What one transformation will this be the same as?
  ::方形在以 79 角度相交的两条线上反射。 哪种变形和哪一种变形相同 ?

  播放段落

  From the Reflection over Intersecting Lines Theorem, this is the same as a rotation of $\begin{array}{r}2\cdot {79}^{\circ }={178}^{\circ }\end{array}$ .
  ::从交叉线理论的反射来看,这与279178的旋转相同。

  播放段落

  Example 5
  ::例5

  播放段落

  $\begin{array}{r}\mathrm{△}DEF\end{array}$ has vertices $\begin{array}{r}D(3,-1),E(8,-3)\end{array}$ , and $\begin{array}{r}F(6,4)\end{array}$ . Reflect $\begin{array}{r}\mathrm{△}DEF\end{array}$ over $\begin{array}{r}x=-5\end{array}$ and then $\begin{array}{r}x=1\end{array}$ . Determine which one translation this double reflection would be the same as.
  ::DEF有D(3)-1,E(8)-3和F(6,4)的顶部,在 x5 上反射 DEF 然后x=1. 确定这种双重反射的翻译与哪一种相同 。

  播放段落

  From the Reflections over Parallel Lines Theorem, we know that this double reflection is going to be the same as a single translation of $\begin{array}{r}2(1-(-5))\end{array}$ or 12 units.
  ::从平行线理论的反射中,我们知道这种双重反射与2(1至(5)或12个单位的单一译文相同。

  

  播放段落

  Example 6
  ::例6

  播放段落

  Reflect $\begin{array}{r}\mathrm{△}DEF\end{array}$ from Question 2 over the $\begin{array}{r}x-\end{array}$ axis, followed by the $\begin{array}{r}y-\end{array}$ axis. Find the coordinates of $\begin{array}{r}\mathrm{△}{D}^{″}{E}^{″}{F}^{″}\end{array}$ and the one transformation this double reflection is the same as.
  ::从问题2中反射 X - 轴的 Z- DEF , 后面是 y - 轴。 找到 Q- D 的坐标 。 找到这个双重反射的转换和 y - 轴的坐标相同 。

  播放段落

  $\begin{array}{r}\mathrm{△}{D}^{″}{E}^{″}{F}^{″}\end{array}$ is the green triangle in the graph to the left. If we compare the coordinates of it to $\begin{array}{r}\mathrm{△}DEF\end{array}$ , we have:
  ::“DEF”是图向左的绿色三角形。如果我们将坐标与“DEF”比较,我们就有:

  

  播放段落

  $$\begin{array}{rl}D(3,-1)& \to D^{″}(-3,1)\\ E(8,-3)& \to E^{″}(-8,3)\\ F(6,4)& \to F^{″}(-6,-4)\end{array}$$

  
  ::D(3,-1)-(D)-(D)-(-)-(3,1)-(E)-(8)-(E)-(-8,3)-(E)-(-8,3)-(F)-6,4)-(F)-(-6)-(4)

  播放段落

  Review
  ::回顾

  播放段落
  1. Explain why the composition of two or more isometries must also be an isometry.
     ::解释为什么两个或两个以上异类的构成也必须是异度测量。
  播放段落
  2. What one transformation is the same as a reflection over two parallel lines?
     ::一种转变与两种平行线的反射相同吗?
  播放段落
  3. What one transformation is the same as a reflection over two intersecting lines?
     ::两种交叉线的反射是相同的?

  播放段落

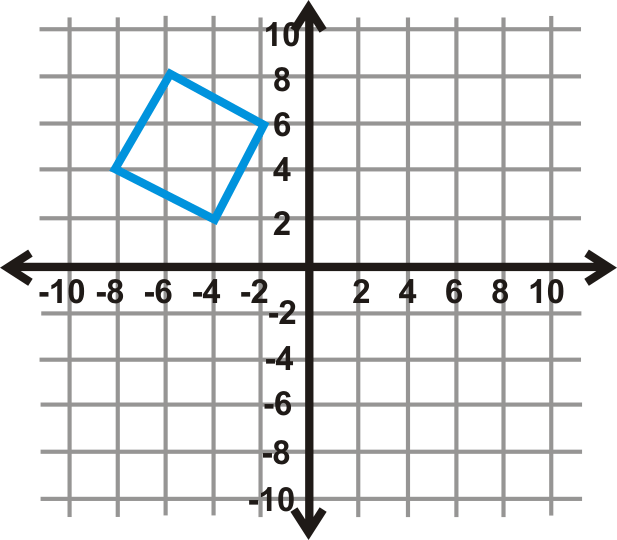
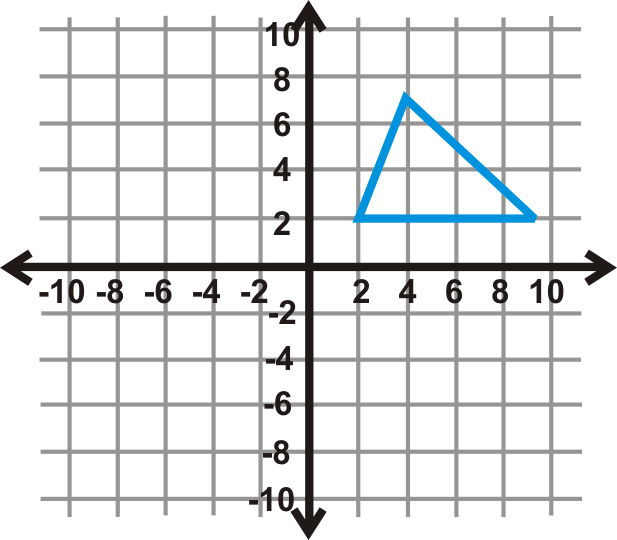
  Use the graph of the square to the left to answer questions 4-6.
  ::使用左边方形图解答问题4-6。

  

  播放段落
  4. Perform a glide reflection over the $\begin{array}{r}x-\end{array}$ axis and to the right 6 units. Write the new coordinates.
     ::在 x- 轴和右边的 6 个单位上执行滑翔反射。 写入新的坐标 。
  播放段落
  5. What is the rule for this glide reflection?
     ::这种滑翔反射有什么规则?
  播放段落
  6. What glide reflection would move the image back to the preimage?
     ::什么样的滑翔反射会让图像回到预映中?

  播放段落

  Use the graph of the square to the left to answer questions 7-9.
  ::使用左边方形图解答问题 7 -9。

  

  播放段落
  7. Perform a glide reflection to the right 6 units, then over the $\begin{array}{r}x-\end{array}$ axis. Write the new coordinates.
     ::向右侧的 6 个单位进行滑翔反射,然后在 x- 轴上方进行。 写入新的坐标 。
  播放段落
  8. What is the rule for this glide reflection?
     ::这种滑翔反射有什么规则?
  播放段落
  9. Is the rule in #8 different than the rule in #5? Why or why not?
     ::8中的规则和5中的规则不同吗?

  播放段落

  Use the graph of the triangle to the left to answer questions 10-12.
  ::使用左侧三角形的图解回答问题 10-12 。

  

  播放段落
  10. Perform a glide reflection over the $\begin{array}{r}y-\end{array}$ axis and down 5 units. Write the new coordinates.
      ::在 y- 轴 和 5 个单位上执行滑翔反射。 写入新的坐标 。
  播放段落
  11. What is the rule for this glide reflection?
      ::这种滑翔反射有什么规则?
  播放段落
  12. What glide reflection would move the image back to the preimage?
      ::什么样的滑翔反射会让图像回到预映中?

  播放段落

  Use the graph of the triangle to the left to answer questions 13-15.
  ::使用左侧三角形的图解回答问题13-15。

  

  播放段落
  13. Reflect the preimage over $\begin{array}{r}y=-1\end{array}$ followed by $\begin{array}{r}y=-7\end{array}$ . Write the new coordinates of the reflected image.
      ::反映 y1 的预映图,然后是 y7 。 写 反映图像的新坐标 。
  播放段落
  14. What one transformation is this double reflection the same as?
      ::这种双重反射与什么变化相同?
  播放段落
  15. Write the rule.
      ::写下规则

  播放段落

  Use the graph of the triangle to the left to answer questions 16-18.
  ::使用左侧三角形的图解回答问题16-18。

  

  播放段落
  16. Reflect the preimage over $\begin{array}{r}y=-7\end{array}$ followed by $\begin{array}{r}y=-1\end{array}$ . Write the new coordinates of the reflected image.
      ::映射 y 7 的预景 依次于 y 1 。 写下 反映图像的新坐标 。
  播放段落
  17. What one transformation is this double reflection the same as?
      ::这种双重反射与什么变化相同?
  播放段落
  18. Write the rule.
      ::写下规则
  播放段落
  19. How do the final triangles in #13 and #16 differ?
      ::13和16中的最后三角形有何不同?

  播放段落

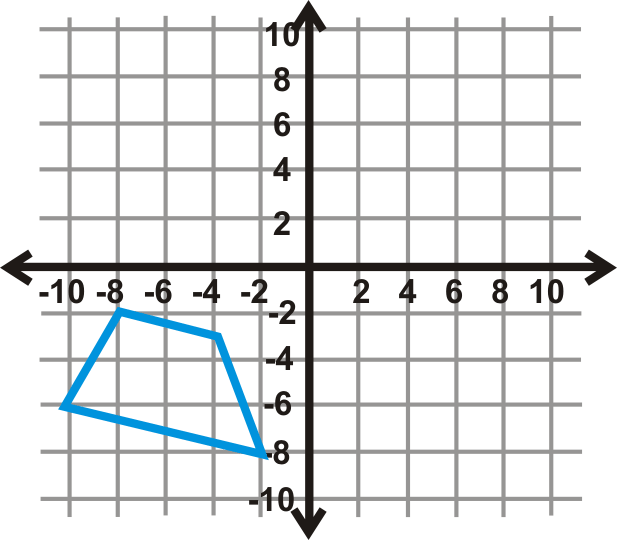
  Use the trapezoid in the graph to the left to answer questions 20-22.
  ::使用图中左侧的图层图解来回答问题20-22。

  

  播放段落
  20. Reflect the preimage over the $\begin{array}{r}x-\end{array}$ axis then the $\begin{array}{r}y-\end{array}$ axis. Write the new coordinates of the reflected image.
      ::反射 X - 轴的预映像, 然后是 y - 轴。 写入反射图像的新坐标 。
  播放段落
  21. Now, start over. Reflect the trapezoid over the $\begin{array}{r}y-\end{array}$ axis then the $\begin{array}{r}x-\end{array}$ axis. Draw this trapezoid.
      ::现在,从头开始。在 y - 轴上反射捕捉类体,然后是 x - 轴。 绘制这个捕捉类体 。
  播放段落
  22. Are the final trapezoids from #20 and #21 different? Why do you think that is?
      ::20号和21号最后的捕捉类动物有不同吗?

  播放段落

  Answer the questions below. Be as specific as you can.
  ::回答以下问题,尽量具体。

  播放段落
  23. Two parallel lines are 7 units apart. If you reflect a figure over both how far apart with the preimage and final image be?
      ::两条平行线是分开的 7 个单位。 如果您能反映一个数字, 显示与预映和最终图像的距离 ?
  播放段落
  24. After a double reflection over parallel lines, a preimage and its image are 28 units apart. How far apart are the parallel lines?
      ::在平行线上进行双反射后,预视和图像是28个单位。平行线之间距离有多远?
  播放段落
  25. Two lines intersect at a $\begin{array}{r}{165}^{\circ }\end{array}$ angle. If a figure is reflected over both lines, what is the measure of the angle between the image and the preimage?
      ::两条线在 165 角度上交叉。 如果一个数字在两条线上反射, 图像和预视之间的角的测量值是多少 ?
  播放段落
  26. What is the center of rotation for #25?
      ::25号的旋转中心是什么?
  播放段落
  27. Two lines intersect at an $\begin{array}{r}{83}^{\circ }\end{array}$ angle. If a figure is reflected over both lines, what is the measure of the angle between the image and the preimage?
      ::两条线在 83 角度上交叉。 如果一个数字在两条线上反射, 图像和预视之间的角的测量值是多少 ?
  播放段落
  28. A preimage and its image are $\begin{array}{r}{244}^{\circ }\end{array}$ apart. If the preimage was reflected over two intersecting lines, at what angle did they intersect?
      ::预映像及其图像是 244 。 如果预映像在两条交叉线上被反射, 它们从哪个角度交叉 ?
  播放段落
  29. A preimage and its image are $\begin{array}{r}{98}^{\circ }\end{array}$ apart. If the preimage was reflected over two intersecting lines, at what angle did they intersect?
      ::预映像及其图像是 98\\\\\\\\\\\\\\\\\"98\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
  播放段落
  30. After a double reflection over parallel lines, a preimage and its image are 62 units apart. How far apart are the parallel lines?
      ::在平行线上进行双反射后,预视和图像是62个单位分开的。平行线相距多远?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。