4.5 三角函数的逆数

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 三角函数的逆数

  Collapse Expand

  三角函数的逆数

  播放段落

  Your instructor gives you a trigonometric function , $\begin{align*}f(x) = 3\sin (x) + 5\end{align*}$ , and asks you to find the inverse. You are all set to start manipulating the equation, when you realize that you don't know just how to do this. Your instructor suggests that you try finding the inverse through graphing instead.
  ::您的教官给了您一个三角函数, f( x)=3sin( x)+5, 并要求您找到反方向。 当您意识到自己并不知道如何做到这一点时, 您的教官建议您尝试通过图形化找到反方向 。

  播放段落

  Are you able to do this?
  ::你能做到吗?

  播放段落

  Finding the Inverse of a Trigonometric Function
  ::查找三角函数的反向

  播放段落

  In other lessons, two different ways to find the inverse of a function were discussed: graphing and algebra. However, when finding the inverse of trig functions, it is easy to find the inverse of a trig function through graphing.
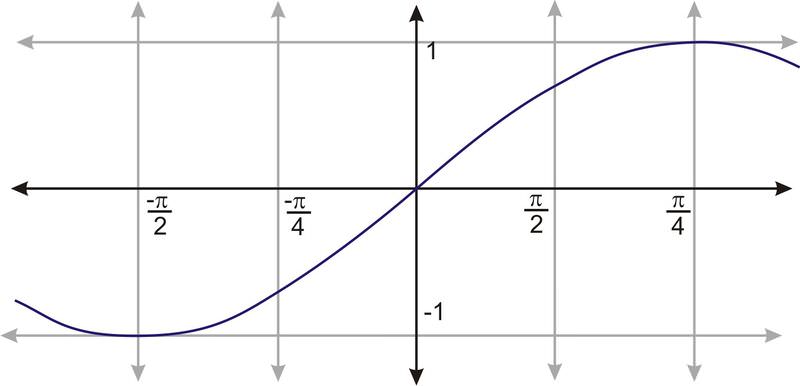
  ::在其他经验教训中,讨论了找到函数反向的两个不同方法:图表和代数。然而,在找到三角函数反向时,很容易通过图表找到三角函数反向。

  播放段落

  Consider the graph of a sine function shown here:
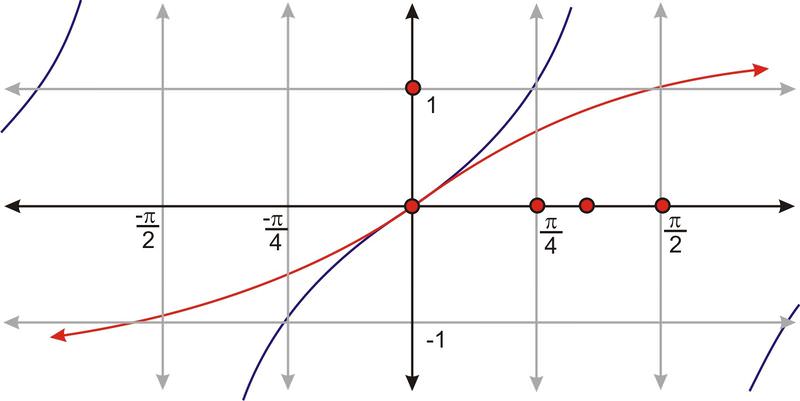
  ::考虑此处显示的正弦函数图 :

  

  播放段落

  In order to consider the inverse of this function, we need to restrict the domain so that we have a section of the graph that is one-to-one. If the domain of $\begin{align*}f\end{align*}$ is restricted to $\begin{align*}-\frac{\pi}{2} \le x \le \frac{\pi}{2}\end{align*}$ a new function $\begin{align*}f(x) = \sin x, -\frac{\pi}{2} \le x \le \frac{\pi}{2}\end{align*}$ . is defined. This new function is one-to-one and takes on all the values that the function $\begin{align*}f(x) = \sin x\end{align*}$ takes on. Since the restricted domain is smaller, $\begin{align*}f(x) = \sin x, -\frac{\pi}{2} \le x \le \frac{\pi}{2}\end{align*}$ takes on all values once and only once.
  ::为了考虑此函数的反向, 我们需要限制域 , 这样我们就可以在图表中有一个一对一的区块。 如果 f 的域限为 @ 2x2, 则定义一个新的函数 f( x) =sinx, 222x。 这个新函数是一对一, 并使用函数 f( x) =sinx 所带的全部值。 因为限制域较小, f( x) =sinx, 2 仅一次接收所有值 。

  

  播放段落

  The inverse of $\begin{align*}f(x)\end{align*}$ is represented by the symbol $\begin{align*}f^{-1}(x)\end{align*}$ , and %20%3D%20x"> $\begin{align*}y = f^{-1}(x) \Leftrightarrow f(y) = x\end{align*}$ . The inverse of $\begin{align*}\sin x, -\frac{\pi}{2} \le x \le \frac{\pi}{2}\end{align*}$ will be written as $\begin{align*}\sin^{-1} x\end{align*}$ . or $\begin{align*}\arcsin x\end{align*}$ .
  ::f( x) 的反义符号为 f-1 (x), 和 y= f- 1 (x) f =x。 sin_x 的反义符号为 sin_x, 2 将写成 sin_ 1 x. 或 arcsin_x 。

  播放段落

  $$\begin{align*}\begin{Bmatrix} y = \sin^{-1} x\\ \quad or\\ y = \arcsin x \end{Bmatrix} \Leftrightarrow \sin y = x\end{align*}$$
  ::{y=sin- 1xory=arcsinxsin=x y=sin_ 1xory=arcsinxsin=x

  播放段落

  In this lesson we will use both $\begin{align*}\sin^{-1} x\end{align*}$ and $\begin{align*}\arcsin x\end{align*}$ and both are read as “the inverse sine of $\begin{align*}x\end{align*}$ ” or “the number between $\begin{align*}-\frac{\pi}{2}\end{align*}$ and $\begin{align*}\frac{\pi}{2}\end{align*}$ whose sine is $\begin{align*}x\end{align*}$ .”
  ::在这个教训中,我们将同时使用 sin-1x 和 arcsinx , 两者都被解读为“x的逆正弦”或“xx是%2和%2之间的数字 ” 。

  播放段落

  The graph of $\begin{align*}y = \sin^{-1} x\end{align*}$ is obtained by applying the inverse reflection principle and reflecting the graph of $\begin{align*}y=\sin x, -\frac{\pi}{2} \le x \le \frac{\pi}{2}\end{align*}$ in the line $\begin{align*}y = x\end{align*}$ . The domain of $\begin{align*}y = \sin x\end{align*}$ becomes the range of $\begin{align*}y = \sin^{-1} x\end{align*}$ , and hence the range of $\begin{align*}y = \sin x\end{align*}$ becomes the domain of $\begin{align*}y = \sin^{-1} x\end{align*}$ .
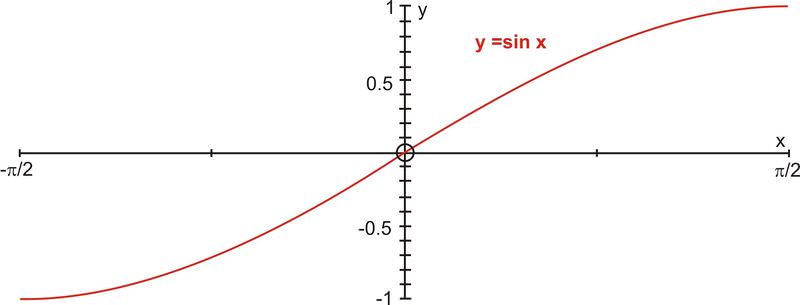
  ::y=sin-1x 的图形通过应用反向反射原理并反映 y=sinx, 2x2 的图形在 y=x 线上获取。 y=sinx 的域成为 y=sin-1x 的域, 因此y=sinx 的域成为 y=sin_1x 的域 。

  

  播放段落

  Another way to view these graphs is to construct them on separate grids. If the domain of $\begin{align*}y = \sin x\end{align*}$ is restricted to the interval $\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$ , the result is a restricted one-to one function. The inverse sine function $\begin{align*}y = \sin^{-1} x\end{align*}$ is the inverse of the restricted section of the sine function.
  ::查看这些图表的另一种方法是在不同的网格上构造这些图。如果 y=sinx 的域限为间隔 [2,%2],结果则是一个限制一对一的函数。反正弦函数 y=sin-1x 是正弦函数的反面部分 。

  

  播放段落

  The domain of $\begin{align*}y = \sin x\end{align*}$ is $\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$ and the range is [-1, 1].
  ::y=sinx的域是[2,2],范围是[-1,1]。

  播放段落

  The restriction of $\begin{align*}y = \sin x\end{align*}$ is a one-to-one function and it has an inverse that is shown below.
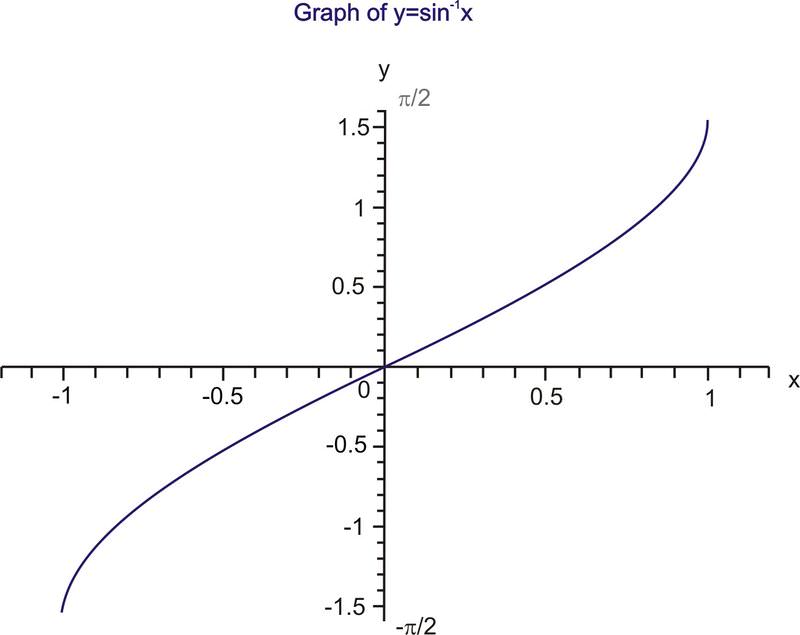
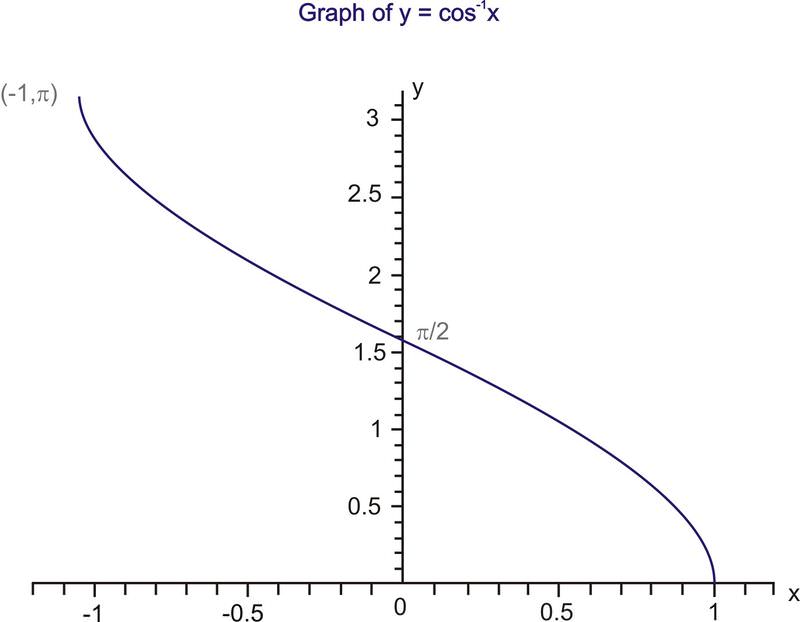
  ::y=sinx 的限制是一对一的函数,其反函数如下所示。

  

  播放段落

  The domain of $\begin{align*}y = \sin^{-1}\end{align*}$ is [-1, 1] and the range is $\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$ .
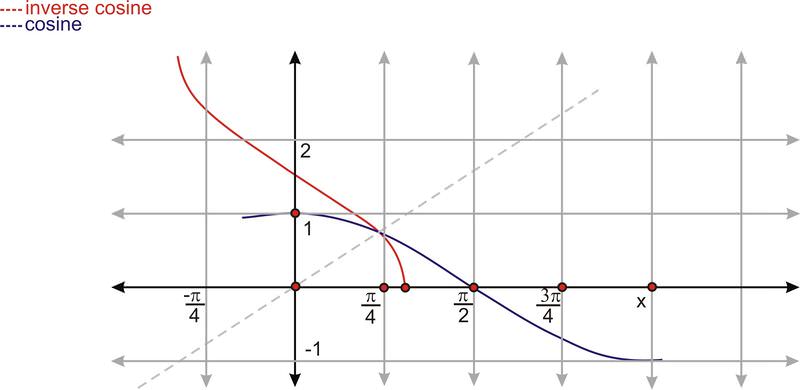
  ::y=sin-1is [-1,1] 域,范围为[2,%2] 。

  播放段落

  The inverse functions for cosine and tangent are defined by following the same process as was applied for the inverse sine function. However, in order to create one-to-one functions, different intervals are used. The cosine function is restricted to the interval $\begin{align*}0 \le x \le \pi\end{align*}$ and the new function becomes $\begin{align*}y = \cos x, 0 \le x \le \pi\end{align*}$ . The inverse reflection principle is then applied to this graph as it is reflected in the line $\begin{align*}y = x\end{align*}$ The result is the graph of $\begin{align*}y = \cos^{-1} x\end{align*}$ (also expressed as $\begin{align*}y = \arccos x\end{align*}$ ).
  ::余弦函数和正切函数的反向函数由对正弦函数适用的相同进程来定义。然而,为了创建一对一函数,则使用不同的间隔。余弦函数限于间距 0x ,新的函数为 y=cosx, 0x 。然后对这个图应用反向反向原则,因为它反映在 y=x 线中。结果为 y=cos-1x 的图形(也表示为 y=arccosx )。

  

  播放段落

  Again, construct these graphs on separate grids to determine the domain and range. If the domain of $\begin{align*}y = \cos x\end{align*}$ is restricted to the interval $\begin{align*}[0, \pi]\end{align*}$ , the result is a restricted one-to one function. The inverse cosine function $\begin{align*}y = \cos^{-1} x\end{align*}$ is the inverse of the restricted section of the cosine function.
  ::再次在单独的网格上构造这些图形,以决定域和范围。如果 y=cosx 的域限为间距 [0,%] , 则结果为限制一对一的函数。 逆余弦函数 y=cos- 1,%x 是余弦函数的反面部分 。

  

  播放段落

  The domain of $\begin{align*}y = \cos x\end{align*}$ is $\begin{align*}[0, \pi]\end{align*}$ and the range is [-1, 1].
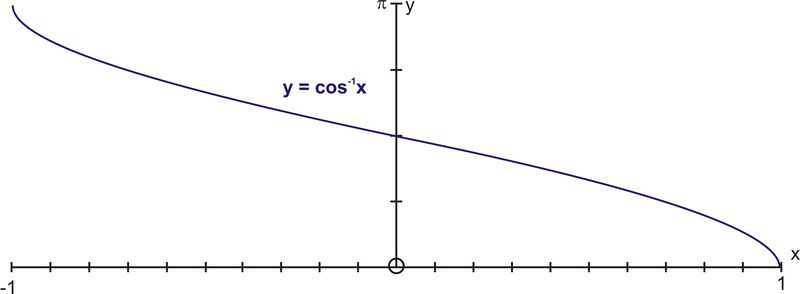
  ::y=cosx 的域为 [0,_] , 范围为 [1, 1] 。

  播放段落

  The restriction of $\begin{align*}y = \cos x\end{align*}$ is a one-to-one function and it has an inverse that is shown below.
  ::Y=cosx 的限制是一对一的函数,其反函数如下所示。

  

  播放段落

  The statements $\begin{align*}y = \cos x\end{align*}$ and $\begin{align*}x = \cos y\end{align*}$ are equivalent for $\begin{align*}y-\end{align*}$ values in the restricted domain $\begin{align*}[0, \pi]\end{align*}$ and $\begin{align*}x-\end{align*}$ values between -1 and 1.
  ::声明y=cosxandx=cossyare 等值的工龄值,在限制域 [0,] 和x- 值 -1 和 1 之间。

  播放段落

  The domain of $\begin{align*}y = \cos^{-1} x\end{align*}$ is [-1, 1] and the range is $\begin{align*}[0, \pi]\end{align*}$ .
  ::y=cos-1x的域为[-1,1],范围为[0,_]。

  播放段落

  The tangent function is restricted to the interval $\begin{align*}-\frac{\pi}{2} < x < \frac{\pi}{2}\end{align*}$ and the new function becomes $\begin{align*}y = \tan x, -\frac{\pi}{2} < x < \frac{\pi}{2}\end{align*}$ . The inverse reflection principle is then applied to this graph as it is reflected in the line $\begin{align*}y = x\end{align*}$ . The result is the graph of $\begin{align*}y = \tan^{-1} x\end{align*}$ (also expressed as $\begin{align*}y = \arctan x\end{align*}$ ).
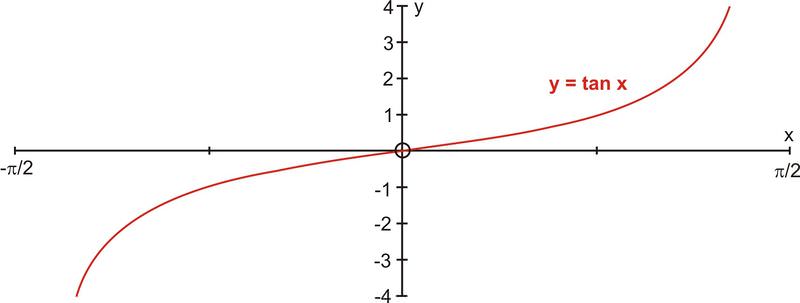
  ::相切函数仅限于 2 < x2 间隔, 而新函数则成为 y=tanx,\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  

  播放段落

  Graphing the two functions separately will help us to determine the domain and range. If the domain of $\begin{align*}y = \tan x\end{align*}$ is restricted to the interval $\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$ , the result is a restricted one-to one function. The inverse tangent function $\begin{align*}y = \tan^{-1} x\end{align*}$ is the inverse of the restricted section of the tangent function.
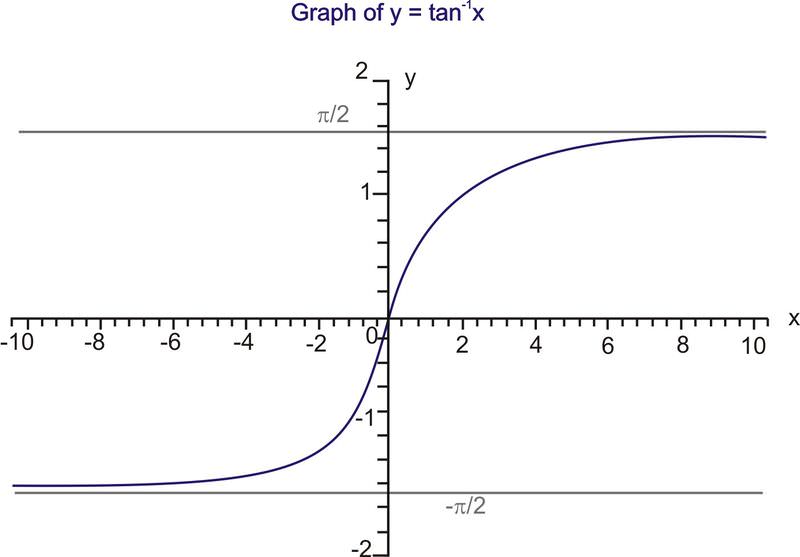
  ::将两个函数分开图形将帮助我们确定域和范围。如果 y=tanx 的域限于间隔 [2, 2] , 则结果为一对一的限制函数。 反正切函数 y=tan-1x 是正切函数限制部分的反向函数 。

  

  播放段落

  The domain of $\begin{align*}y = \tan x\end{align*}$ is $\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$ and the range is $\begin{align*}[-\infty, \infty]\end{align*}$ .
  ::y=tanx的域是[2,2],范围是[,]。

  播放段落

  The restriction of $\begin{align*}y = \tan x\end{align*}$ is a one-to-one function and it has an inverse that is shown below.
  ::y=tanx的限制是一对一的函数,其反函数如下所示。

  

  播放段落

  The statements $\begin{align*}y = \tan x\end{align*}$ and $\begin{align*}x = \tan y\end{align*}$ are equivalent for $\begin{align*}y-\end{align*}$ values in the restricted domain $\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$ and $\begin{align*}x-\end{align*}$ values between -4 and +4.
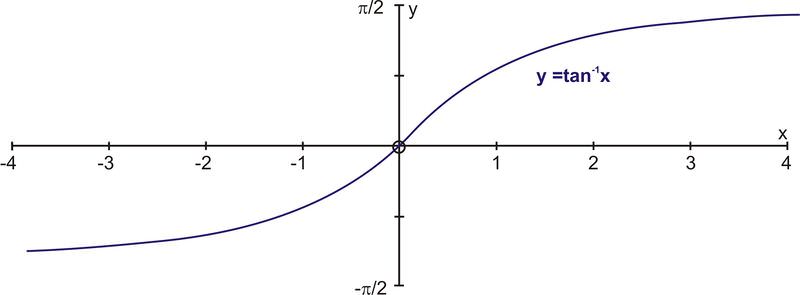
  ::限制域[2,2] 和 -4和+4之间的声明y=tanxandx=tanyare等值的表面值[2,2]和x-数值。

  播放段落

  The domain of $\begin{align*}y = \tan^{-1} x\end{align*}$ is $\begin{align*}[-\infty, \infty]\end{align*}$ and the range is $\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$ .
  ::y=tan-1x的域是[,],范围是[2,2]。

  播放段落

  The above information can be readily used to evaluate inverse trigonometric functions without the use of a calculator. These calculations are done by applying the restricted domain functions to the unit circle . To summarize:
  ::上述信息可以很容易地用于评价反三角函数,而不使用计算器。这些计算方法是对单位圆应用限制的域函数。

  Restricted Domain Function	Inverse Trigonometric Function	Domain	Range	Quadrants
  $\begin{align*}y = \sin x\end{align*}$		$\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$	[-1, 1]	1 AND 4
  	播放段落 $\begin{align*}y = \arcsin x\end{align*}$ ::y=arcsinx 播放段落 $\begin{align*}y = \sin^{-1} x\end{align*}$ ::y=sin-1x	[-1, 1]	$\begin{align*}\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]\end{align*}$
  $\begin{align*}y = \cos x\end{align*}$		$\begin{align*}[0, \pi]\end{align*}$	[-1, 1]	1 AND 2
  	播放段落 $\begin{align*}y = \arccos x\end{align*}$ ::y=arccosx 播放段落 $\begin{align*}y = \cos^{-1} x\end{align*}$ ::y=cos-1x	[-1, 1]	$\begin{align*}[0, \pi]\end{align*}$
  $\begin{align*}y = \tan x\end{align*}$		$\begin{align*}\left ( -\frac{\pi}{2}, \frac{\pi}{2} \right )\end{align*}$	$\begin{align*}(-\infty, \infty)\end{align*}$	1 AND 4
  	播放段落 $\begin{align*}y = \arctan x\end{align*}$ ::y=arctanx 播放段落 $\begin{align*}y = \tan^{-1}x\end{align*}$ ::y'tan-1x	$\begin{align*}(-\infty, \infty)\end{align*}$	$\begin{align*}\left ( -\frac{\pi}{2}, \frac{\pi}{2} \right )\end{align*}$

  播放段落

  Now that the three trigonometric functions and their inverses have been summarized, let’s take a look at the graphs of these inverse trigonometric functions.
  ::现在,三个三角函数及其反向已被总结,让我们看看这些反三角函数的图表。

  

  

  

  播放段落

  Let's take a look at a few example problems. 
  ::让我们来看一下几个例子问题。

  播放段落

  1. Establish an alternative domain that makes $\begin{align*}y=\sin(x)\end{align*}$ a one to one function .
  ::1. 建立一个使y=sin(x)成为一对一函数的替代域。

  播放段落

  Any number of possible solutions can be given, but the important point is that the function must pass the "horizontal line test" and the "vertical line test". This means that a horizontal line drawn through the graph will intersect the function in only one place, and a vertical line drawn through the graph will intersect the function in only one place.
  ::任何可能的解决方案都可以给出, 但重要的一点是, 函数必须经过“ 水平线测试” 和“ 垂直线测试 ” 。 这意味着通过图形绘制的水平线将仅在一个地方交叉函数, 而通过图形绘制的垂直线将仅在一个地方交叉函数 。

  播放段落

  For the sine curve, this means that the function can't "turn over" or "go in the other direction", since then it couldn't pass the horizontal line test . So any part of the function that starts at the bottom of the "y" values and stops at the top of the "y" values will work. (Any value that starts at the top of the "y" values and stops at the bottom of the "y" values will work as well.
  ::对于正弦曲线, 这意味着函数不能“ 翻转” 或“ 往另一方向走 ” , 自此无法通过水平线测试 。 因此, 从“ y” 值底部开始并在“ y” 值顶部停止的函数的任何部分都会有效 。 (任何从“ y” 值顶部开始并在“ y” 值底部停止的值也将有效 。

  

  播放段落

  In this problem, you can see that the function starts at $\begin{align*}\frac{\pi}{2}\end{align*}$ and stops at $\begin{align*}\frac{3\pi}{2}\end{align*}$ .
  ::在此问题上, 您可以看到此函数的起始时间为 2, 停止时间为 32 。

  播放段落

  2. Find the range of the function given in  the previous problem.
  ::2. 查找上一个问题中给定的函数范围。

  播放段落

  You can see that the function still has the same "y" range of values, since the function $\begin{align*}y = \sin x\end{align*}$ moves up and down between -1 and 1. Therefore, the range is $\begin{align*}-1 \le y \le 1\end{align*}$ .
  ::您可以看到,函数的值范围仍然相同,因为 y=sinx 函数在 -1 和 1 之间向上和向下移动。 因此,范围是 - 1y1 。

  播放段落

  3. Find the domain and range of the inverse of the function given in  the first problem.
  ::3. 找出第一个问题中给定函数的逆差的域和范围。

  播放段落

  Since the domain of the inverse function is the range of the original function and the range of the inverse function is the domain of the original function, you only have to take the "x" and "y" values of the original function and reverse them to get the domain and range of the inverse function.
  ::由于反函数的域是原始函数的范围,而反函数的范围是原始函数的范围,所以只需要使用原始函数的“x”和“y”值,然后将其反转,才能获得反函数的域和范围。

  播放段落

  Therefore, the domain of $\begin{align*}y = \sin^{-1} x\end{align*}$ as described in #1 is $\begin{align*}-1 \le x \le 1\end{align*}$ and the range is $\begin{align*}\frac{\pi}{2} \le y \le \frac{3\pi}{2}\end{align*}$ .
  ::因此,如第1页所述,y=sin-1x的域为-1x1,范围为 232。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find the inverse of a function. 
  ::早些时候,有人要求你找出函数的反面。

  播放段落

  To find the inverse of this function through graphing, first restrict the domain of the function so that it is one to one. A graph of $\begin{align*}f(x) = 3\sin (x) + 5\end{align*}$ , restricted so that the domain is $\begin{align*}-\frac{\pi}{2}\end{align*}$ to $\begin{align*}\frac{\pi}{2}\end{align*}$ looks like this:
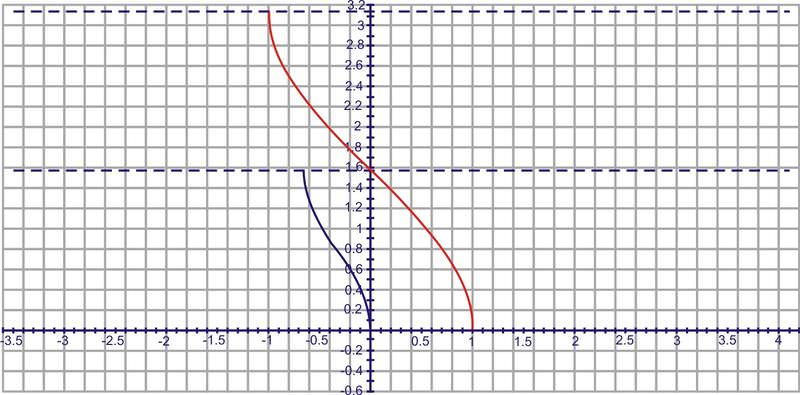
  ::要通过图形化找到此函数的反向, 请先将函数的域限制为一到一。 f( x) =3sin( x) +5 的图形将限制此函数的反向, 使域为% 2 到% 2 看起来像 :

  

  播放段落

  If you apply the inverse reflection principle, you can see that the inverse of this function looks like this:
  ::如果您应用反向反反射原则, 您可以看到此函数的反向看起来像 :

  

  播放段落

  Example 2
  ::例2

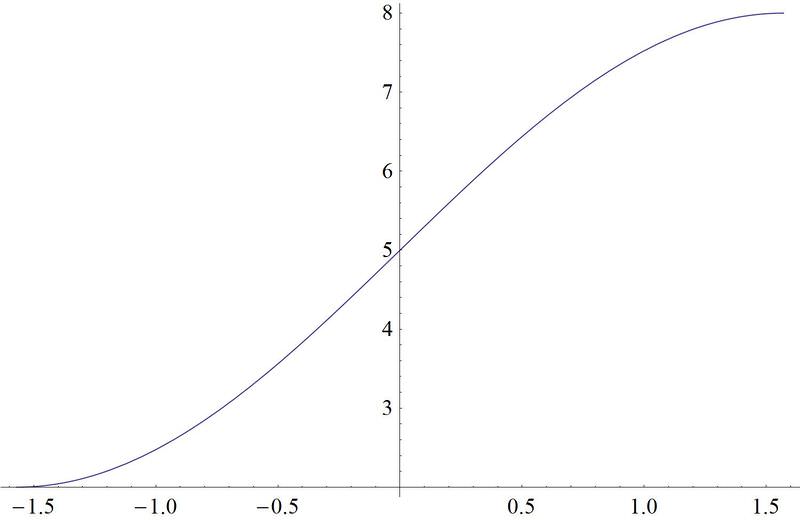
  播放段落

  Sketch a graph of $\begin{align*}y = \frac{1}{2} \cos^{-1} (3x+1)\end{align*}$ . Sketch $\begin{align*}y = \cos^{-1} x\end{align*}$ on the same set of axes and compare how the two differ.
  ::在同一组轴上绘制 y= 12cos- 1( 3x+1) 的图形, 并比较两者的不同 。

  播放段落

  $\begin{align*}y = \frac{1}{2} \cos^{-1} (3x+1)\end{align*}$ is in blue and $\begin{align*}y =\cos^{-1}(x)\end{align*}$ is in red. Notice that $\begin{align*}y = \frac{1}{2} \cos^{-1}(3x+1)\end{align*}$ has half the and is shifted over -1. The 3 seems to narrow the graph.
  ::y=12cos- 1( 3x+1) 蓝色, y=cos- 1( x) 红色。 注意 y= 12cos- 1( 3x+1) 拥有一半, 并被移到 - 1 上。 3 似乎缩小了图形 。

  

  播放段落

  Example 3
  ::例3

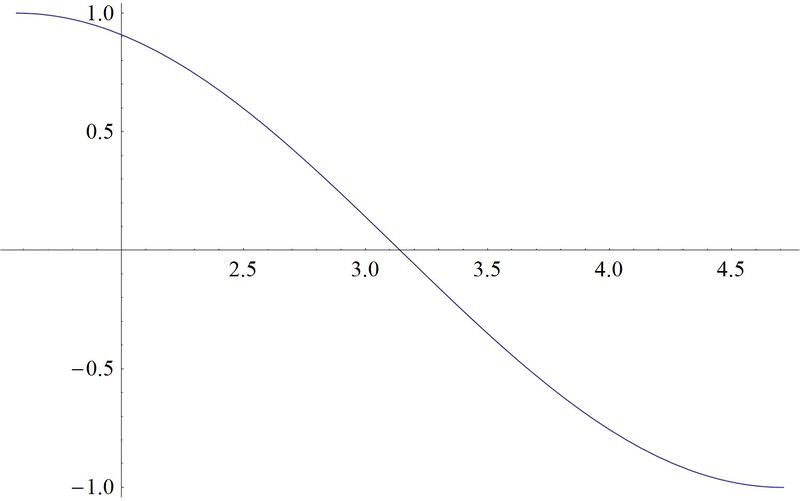
  播放段落

  Sketch a graph of $\begin{align*}y = 3-\tan^{-1} (x-2)\end{align*}$ . Sketch $\begin{align*}y = \tan^{-1} x\end{align*}$ on the same set of axes and compare how the two differ.
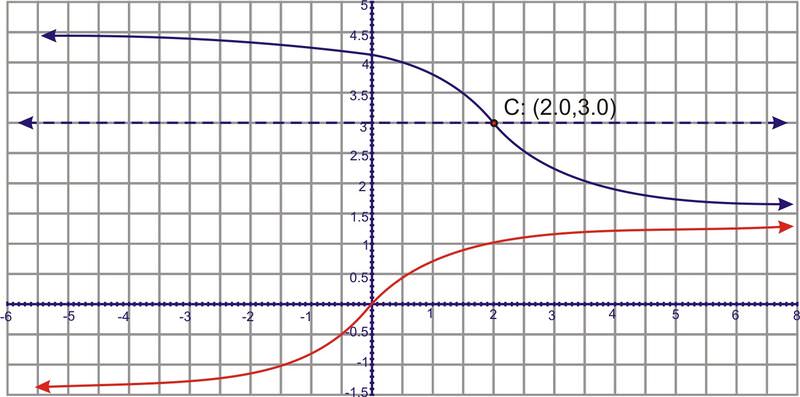
  ::在同一组轴上绘制 y = 3 -tan - 1 (x-2) 的图,并比较两者的不同。

  播放段落

  $\begin{align*}y = 3-\tan^{-1} (x-2)\end{align*}$ is in blue and $\begin{align*}y = \tan^{-1} x\end{align*}$ is in red. $\begin{align*}y = 3-\tan^{-1} (x-2)\end{align*}$ is shifted up 3 and to the right 2 (as indicated by point $\begin{align*}C\end{align*}$ , the “center”) and is flipped because of the $\begin{align*}-\tan^{-1}\end{align*}$ .
  ::y=3-tan-1(x-2)是蓝色的,y=tan-1x是红色的。y=3-tan-1(x-2)被移到3和右边2(如“中心”C点所示),并因-tan-1而翻转。

  

  播放段落

  Example 4
  ::例4

  播放段落

  Graph $\begin{align*}y = 2\sin^{-1}(2x)\end{align*}$
  ::图 y= 2sin - 1 ( 2x)

  

  播放段落

  Review
  ::回顾

  播放段落
  1. Why does the domain of a trigonometric function have to be restricted in order to find its inverse function?
     ::为什么要限制三角函数领域才能发现其反作用?
  播放段落
  2. If the domain of $\begin{align*}f(x)=\cos(x)\end{align*}$ is $\begin{align*}[0,\pi]\end{align*}$ , what is the domain and range of $\begin{align*}f^{-1}(x)\end{align*}$ ?.
     ::如果 f(x) =cos(x) 的域是 [0, 则f- 1(x) 的域和范围是什么?
  播放段落
  3. If the domain of $\begin{align*}g(x)=\sin(x)\end{align*}$ is $\begin{align*}[-\frac{\pi}{2},\frac{\pi}{2}]\end{align*}$ , what is the domain and range of $\begin{align*}g^{-1}(x)\end{align*}$ ?.
     ::如果 g(x) =sin(x) 的域是 [2,%2] , g-1(x) 的域和范围是什么?
  播放段落
  4. Establish an alternative domain that makes $\begin{align*}y=\cos(x)\end{align*}$ a function.
     ::建立一个使y=cos(x) 函数成为函数的替代域 。
  播放段落
  5. What is the domain and range of the inverse of the function from the previous problem.
     ::函数从上一个问题反向的域和范围是什么 。
  播放段落
  6. Establish an alternative domain that makes $\begin{align*}y=\tan(x)\end{align*}$ a function.
     ::建立一个使 y=tan(x) 函数成为 y=tan(x) 的替代域 。
  播放段落
  7. What is the domain and range of the inverse of the function from the previous problem.
     ::函数从上一个问题反向的域和范围是什么 。

  播放段落

  Sketch a graph of each function. Use the domains presented in this concept.
  ::绘制每个函数的图形。 使用此概念中显示的域 。

  播放段落
  8. $\begin{align*}y=2\sin^{-1}(3x-1)\end{align*}$
     ::y=2sin- 1 ( 3x- 1)
  播放段落
  9. $\begin{align*}y=-3+\cos^{-1}(2x)\end{align*}$
     ::y3+cos- 1( 2x)
  播放段落
  10. $\begin{align*}y=1+2\tan^{-1}(x+2)\end{align*}$
      ::y=1+2tan- 1(x+2)
  播放段落
  11. $\begin{align*}y=4\sin^{-1}(x-4)\end{align*}$
      ::y=4sin-1(x-4)
  播放段落
  12. $\begin{align*}y=2+\cos^{-1}(x+3)\end{align*}$
      ::y=2+cos-1(x+3)
  播放段落
  13. $\begin{align*}y=1+\cos^{-1}(2x-3)\end{align*}$
      ::y= 1+cos- 1( 2x- 3)
  播放段落
  14. $\begin{align*}y=-3+\tan^{-1}(3x+1)\end{align*}$
      ::y3+tan- 1( 3x+1)
  播放段落
  15. $\begin{align*}y=-1+2\sin^{-1}(x+5)\end{align*}$
      ::y1+2sin -1(x+5)

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。