1.1 真实数字子集

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 真实数字的子集

  Collapse Expand

  真实数字的子集

  播放段落

  The number of survey participants who declined to respond can be represented by the decimal 0.14141414... How would you write this decimal as a fraction ?
  ::拒绝答复的受访者人数可以用小数点0.14141414表示...您如何将小数点写成小数点?

  播放段落

  By being able to write a repeating decimal as fraction, we know it is a rational number .
  ::通过能够将重复的十进制写成分数, 我们知道这是一个合理的数字。

  播放段落

  Real Numbers
  ::实际数字

  播放段落

  There are several types of real numbers. You are probably familiar with fractions, decimals, integers , whole numbers and even square roots. All of these types of numbers are real numbers. There are two main types of numbers: real and complex. We will address real numbers in this concept.
  ::实际数字有几种类型。 您可能熟悉分数、 小数、 整数、 整数甚至正方根。 所有这些类型的数字都是真实数字。 数字有两大类: 真实的和复杂的。 我们将在这个概念中处理实际数字 。

  Real Numbers	Any number that can be plotted on a number line. Symbol: $\begin{array}{r}\mathbb{R}\end{array}$	Examples: $\begin{array}{r}8,4.67,-\frac{1}{3},\pi \end{array}$
  Rational Numbers	Any number that can be written as a fraction, including repeating decimals. Symbol: $\begin{array}{r}\mathbb{Q}\end{array}$	Examples: $\begin{array}{r}-\frac{5}{9},\frac{1}{8},1.\bar{3},\frac{16}{4}\end{array}$
  Irrational Numbers	Real numbers that are not rational. When written as a decimal, these numbers do not end nor repeat.	Example: $\begin{array}{r}e,\pi ,-\sqrt{2},\sqrt[3]{5}\end{array}$
  Integers	All positive and negative “counting” numbers and zero. Symbol: $\begin{array}{r}\mathbb{Z}\end{array}$	Example: -4, 6, 23, -10
  Whole Numbers	All positive “counting” numbers and zero.	Example: 0, 1, 2, 3, ...
  Natural Numbers	All positive “counting” numbers. Symbol: $\begin{array}{r}\mathbb{N}\end{array}$	Example: 1, 2, 3, ...

  播放段落

  A counting number is any number that can be counted on your fingers.
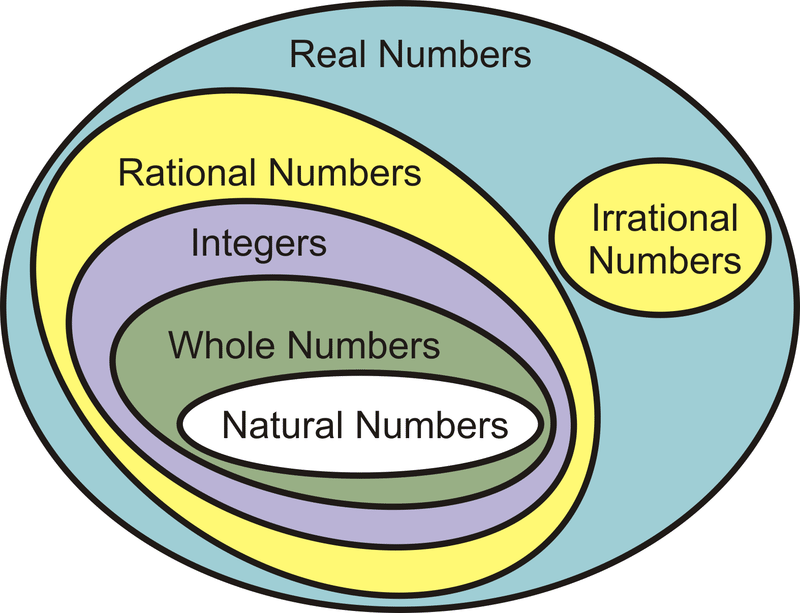
  ::计数数字是指指头可以计数的任何数字。

  播放段落

  The real numbers can be grouped together as follows:
  ::实际数字可分类如下:

  

  播放段落

  Now, let's do the following problems using the different subset of real numbers. 
  ::现在,让我们用真实数字的不同子集 来做下面的问题。

  播放段落
  1. What is the most specific subset of the real numbers that -7 is a part of?
     ::7 -7是真实数字的一部分,其中最具体的子集是什么?

  播放段落

   -7 is an integer.
  ::-7是整数

  播放段落
  2. List all the subsets that 1.3 lies in.
     ::列出1.3中的所有子集 。

  播放段落

  1.3 is a terminating decimal. Therefore , it is considered a rational number. It would also be a real number . As a fraction, we would write $\begin{array}{r}1\frac{3}{10}\end{array}$ because the 3 is in the tenths position after the decimal.
  ::1. 3 是一个终止的小数小数。 因此, 它被认为是一个合理的数字, 也可以是一个真实的数字。 作为小数, 我们会写1310, 因为小数点后, 3 位居十分之一 。

  播放段落
  3. True or False: $\begin{array}{r}\frac{8}{3}\end{array}$ is a rational number.
     ::真理或假:83是一个合理的数字。

  播放段落

  Yes, by definition, because it is written as a fraction.
  ::是的,顾名思义,因为它是作为一个分数写成的。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to write 0.14141414.... as a fraction.
  ::早些时候,你被要求写0.14141414... ...作为一个分数。

  播放段落

  Let's devise a step-by-step process.
  ::让我们设计一个逐步的过程。

  播放段落

  Step 1: Set your repeating decimal equal to x .

  $$\begin{array}{r}x=0.14141414\end{array}$$

  
  ::第1步:将重复的小数小数数设为 x. x=0. 14.141414

  播放段落

  Step 2: Find the repeating digit(s).
  ::第2步:查找重复的数字。

  播放段落

  In this case 14 is repeating.
  ::在这种情况下,14个案件重复。

  播放段落

  Step 3: Move the repeating digits to the left of the decimal point and leave the remaining digits to the right.
  ::第3步:将重复的数字移到小数点左边,将其余的数字移到右边。

  $$\begin{array}{r}14.14141414\end{array}$$

  播放段落

  Step 4: Multiply x by the same factor you multiplied your original repeating decimal to get your new repeating decimal.
  ::第4步:乘以X乘以与乘以原来的重复小数位数相同的因数,以获得新的重复小数位数。

  $$\begin{array}{r}14.14141414=100(0.14141414)\end{array}$$

  播放段落

  So,

  $$\begin{array}{r}100x=14.14141414\end{array}$$

  
  ::所以,100x=14.14141414

  播放段落

  Step 5: Solve your system of linear equations for x .
  ::步骤5:解决 x 的线性方程式系统。

  播放段落

  $$\begin{array}{r}(100x=14.14141414)-(x=0.14141414)\end{array}$$

  yields:
  :100x=14.14141414)-(x=0.14141414)产量:

  播放段落

  $$\begin{array}{r}99x=14\end{array}$$

  so $\begin{array}{r}x=\frac{14}{99}\end{array}$
  ::99x=14so x=1499

  播放段落

  Example 2
  ::例2

  播放段落

  Write 0.327272727... as a fraction.
  ::写0.3272722727... 作为一个分数。

  播放段落

  The 0.3 does not repeat. So, rewrite this as $\begin{array}{r}\mathrm{0.727272727...}-0.4\end{array}$ Therefore, the fraction will be:
  ::0. 3 不重复。 所以, 重写为 0. 72727272727272727... - 0. 4。 因此, 分数将是 :

  $$\begin{array}{r}\frac{72}{99}-\frac{4}{10}\\ \frac{8}{11}-\frac{2}{5}\\ \frac{40}{55}-\frac{22}{55}\\ \frac{18}{55}\end{array}$$

  播放段落

  Example 3
  ::例3

  播放段落

  What type of real number is $\begin{array}{r}\sqrt{5}\end{array}$ ?
  ::5是什么样的实际数字?

  播放段落

  $\begin{array}{r}\sqrt{5}\end{array}$ is an irrational number because, when converted to a decimal, it does not end nor does it repeat.
  ::5 是一个不合理的数字,因为当转换为小数点时,它不会结束,也不会重复。

  播放段落

  Example 4
  ::例4

  播放段落

  List all the subsets that -8 is a part of.
  ::列出 - 8 是其中一部分的所有子集 。

  播放段落

   -8 is a negative integer. Therefore, it is also a rational number and a real number.
  ::-8是一个负整数。因此,它也是一个合理的数字和一个真实的数字。

  播放段落

  Example 5
  ::例5

  播放段落

   True or False: $\begin{array}{r}-\sqrt{9}\end{array}$ is an irrational number.
  ::真理或假:-9是一个非理性的数字。

  播放段落

  $\begin{array}{r}-\sqrt{9}=-3\end{array}$ , which is an integer. The statement is false.
  ::- 93, 是一个整数。 语句是虚假的 。

  播放段落

  Review
  ::回顾

  播放段落

  What is the most specific subset of real numbers that the following numbers belong in?
  ::以下数字属于哪些最具体的实际数字子集?

  1. 5.67
  2. $\begin{array}{r}-\sqrt{6}\end{array}$
  3. $\begin{array}{r}\frac{9}{5}\end{array}$
  4. 0
  5. -75
  6. $\begin{array}{r}\sqrt{16}\end{array}$

  播放段落

  List ALL the subsets that the following numbers are a part of.
  ::列出下列数字是其中一部分的所有子集 。

  7. 4
  8. $\begin{array}{r}\frac{6}{9}\end{array}$
  9. $\begin{array}{r}\pi \end{array}$

  播放段落

  Determine if the following statements are true or false.
  ::确定以下声明是真实的还是虚假的。

  播放段落
  10. Integers are rational numbers.
      ::整数是合理数字。
  播放段落
  11. Every whole number is a real number.
      ::每个数字都是真实的数字。
  播放段落
  12. Integers are irrational numbers.
      ::整数是非理性数字
  播放段落
  13. A natural number is a rational number.
      ::自然数字是一个合理的数字。
  播放段落
  14. An irrational number is a real number.
      ::一个非理性的数字是一个真实的数字。
  播放段落
  15. Zero is a natural number.
      ::零是一个自然数字。

  播放段落

  Rewrite the following repeating decimals as fractions.
  ::将以下重复的十进制数重写为分数。

  16. 0.4646464646...
  17. 0.81212121212...
  18. 0.35050505050...
  19. 2.485485485485485...
  20. 1.25141414141414...

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。