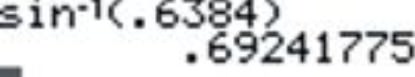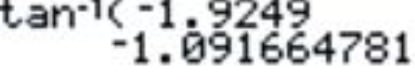Course: 4.7 反对等三角函数的定义

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 反对等三角函数的定义

Collapse Expand
反对等三角函数的定义
So far you've had to deal with trig functions, reciprocal functions, and inverse functions. Now you'll start to see inverse reciprocal functions. For example, can you compute
::到目前为止,你必须处理三角函数、对等函数和反函数。现在你将开始看到反对函数。例如,你能计算

$\begin{aligned} \sec^{- 1} \frac{2}{\sqrt{3}} \end{aligned}$
::空间 - 1+% 23

As it turns out, this can be readily computed.
::事实证明,这可以很容易地计算出来。

Inverse Reciprocal Trigonometric Functions
::反对等三角函数

We already know that the cosecant function is the reciprocal of the sine function. This will be used to derive the reciprocal of the inverse sine function.
::我们已经知道,共生功能是正弦功能的对等功能,这将用来获取反正弦功能的对等功能。

$\begin{aligned} y & = \sin^{- 1} x \\ x & = \sin y \\ \frac{1}{x} & = \csc y \\ \csc^{- 1} \frac{1}{x} & = y \\ \csc^{- 1} \frac{1}{x} & = \sin^{- 1} x \end{aligned}$

::ysin - 1}%x=siny1x=cscycsc -1}%1x=ycsc -1}%1x=sin_1}x=sin=1***x=sin -1**x

Because cosecant and secant are inverses, $\begin{aligned} \sin^{- 1} \frac{1}{x} = \csc^{- 1} x \end{aligned}$ is also true.
::因为和是反的, sin - 11x=csc- 11x也是真实的。

The inverse reciprocal identity for cosine and secant can be proven by using the same process as above. However, remember that these inverse functions are defined by using restricted domains and the reciprocals of these inverses must be defined with the intervals of domain and range on which the definitions are valid.
::使用与上述相同的程序可以证明共生和分离的反对等身份,但是要记住,这些反对功能是通过使用限制的域来界定的,这些反对等功能必须用定义有效的域和范围间隔来界定。

$\begin{aligned} \sec^{- 1} \frac{1}{x} = \cos^{- 1} x \leftrightarrow \cos^{- 1} \frac{1}{x} = \sec^{- 1} x \end{aligned}$

::秒 - 1 1x=cos - 11xxocs - 11xx=sec - 11xx

Tangent and cotangent have a slightly different relationship. Recall that the graph of cotangent differs from tangent by a reflection over the $\begin{aligned} y - \end{aligned}$ axis and a shift of $\begin{aligned} \frac{π}{2} \end{aligned}$ . As an equation, this can be written as $\begin{aligned} \cot x = - \tan (x - \frac{π}{2}) \end{aligned}$ . Taking the inverse of this function will show the inverse reciprocal relationship between arccotangent and arctangent.
::切线和切线之间的关系稍有不同。回顾余切图与正切图不同,反射反射y-axis 和 2 的移动。作为方程式,这可以写为 cotxtan(x2 ) 。如果反观此函数, 则会显示正切和正切之间的反对等关系。

$\begin{aligned} y & = \cot^{- 1} x \\ y & = - \tan^{- 1} (x - \frac{π}{2}) \\ x & = - \tan (y - \frac{π}{2}) \\ - x & = \tan (y - \frac{π}{2}) \\ \tan^{- 1} (- x) & = y - \frac{π}{2} \\ \frac{π}{2} + \tan^{- 1} (- x) & = y \\ \frac{π}{2} - \tan^{- 1} x & = y \end{aligned}$

::y=Cot- 11111(x2)x(y2)-x=tan(y2) tan-1(y2)-(x)=y222+tan-1(-x)=y2-tan-1x=y

Remember that tangent is an odd function , so that $\begin{aligned} \tan (- x) = - \tan (x) \end{aligned}$ . Because tangent is odd, its inverse is also odd. So, this tells us that $\begin{aligned} \cot^{- 1} x = \frac{π}{2} - \tan^{- 1} x \end{aligned}$ and $\begin{aligned} \tan^{- 1} x = \frac{π}{2} - \cot^{- 1} x \end{aligned}$ . To graph arcsecant, arccosecant, and arccotangent in your calculator you will use these conversion identities: $\begin{aligned} \sec^{- 1} x = \cos^{- 1} \frac{1}{x}, \csc^{- 1} x = \sin^{- 1} \frac{1}{x}, \cot^{- 1} x = \frac{π}{2} - \tan^{- 1} x \end{aligned}$ . Note: It is also true that $\begin{aligned} \cot^{- 1} x = \tan^{- 1} \frac{1}{x} \end{aligned}$ .
::记住正切值是一个奇特的函数, 所以 tan (- x) tan (x) 。由于正切值是奇特的, 反正值也是奇特的。因此, 这告诉我们 cot- 1 {x}\\\ \ \ \ \ \ \ \ \ \ \ \ x 和 tan- 1 \ \ \ x 。在计算器中绘制 arcseccant、 arcosecccant 和弧度值时, 您将会使用这些转换特性 : sec- 1 {x= cos - 1 \ \ x, csc- 1 x = sin - 1\ \ \ \ \ x, cot- 1\ \ x \ x 。注意: 注意 : cot- 1 {x=tan_ 1\ x x 。也是正确的。

Finding the Inverse
::查找反向

Find the inverse of $\begin{aligned} \sec^{- 1} \sqrt{2} \end{aligned}$
::查找 sec - 1 @% 2 的反向

Use the inverse reciprocal property. $\begin{aligned} \sec^{- 1} x = \cos^{- 1} \frac{1}{x} \to \sec^{- 1} \sqrt{2} = \cos^{- 1} \frac{1}{\sqrt{2}} \end{aligned}$
::使用反对等属性。秒-1x=cos- 11x{sec- 12=cos- 112

Recall that $\begin{aligned} \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \end{aligned}$ . So, $\begin{aligned} \sec^{- 1} \sqrt{2} = \cos^{- 1} \frac{\sqrt{2}}{2} \end{aligned}$ , and we know that $\begin{aligned} \cos^{- 1} \frac{\sqrt{2}}{2} = \frac{π}{4} \end{aligned}$ . Therefore, $\begin{aligned} \sec^{- 1} \sqrt{2} = \frac{π}{4} \end{aligned}$ .
::回顾12=1222=22。所以, 秒-12=cos-122, 我们知道,cos-122。因此, 秒-124。

Finding the Exact Value
::查找精确值

For each of these problems, first find the reciprocal and then determine the angle from that (without a calculator).
::对于其中的每一个问题,首先要找到对等的,然后(在没有计算器的情况下)从中确定角度。

1. $\begin{aligned} \sec^{- 1} \sqrt{2} \end{aligned}$
::1. 秒-12

$\begin{aligned} \sec^{- 1} \sqrt{2} = \cos^{- 1} \frac{\sqrt{2}}{2} \end{aligned}$ From the unit circle , we know that the answer is $\begin{aligned} \frac{π}{4} \end{aligned}$ .
::根据单位圆,我们知道答案是++4。

2. $\begin{aligned} \cot^{- 1} (- \sqrt{3}) \end{aligned}$
::2. 2-1(-3)

$\begin{aligned} \cot^{- 1} (- \sqrt{3}) = \frac{π}{2} - \tan^{- 1} (- \sqrt{3}) \end{aligned}$ From the unit circle, the answer is $\begin{aligned} \frac{5 π}{6} \end{aligned}$ .
::从单位圆的单位圆中,回答是56。

3. $\begin{aligned} \csc^{- 1} \frac{2 \sqrt{3}}{3} \end{aligned}$
::3. csc-1233

$\begin{aligned} \csc^{- 1} \frac{2 \sqrt{3}}{3} = \sin^{- 1} \frac{\sqrt{3}}{2} \end{aligned}$ Within our interval, there are is one answer, $\begin{aligned} \frac{π}{3} \end{aligned}$ .
::csc-1233=sin-132 在我们的间隔内,只有一个答案,%3。

Using Technology
::使用技术

For each of the following, find the value in radian measure
::对于下列每一种,请查找以弧度计值的数值。

Make sure that your calculator’s MODE is RAD (radians)
::确保您的计算器的 MODE 是RAD( radians) 。

1. $\begin{aligned} \arcsin 0.6384 \end{aligned}$
::1. arcsin 0.6384

2. $\begin{aligned} \arccos (- 0.8126) \end{aligned}$
::2. arccos(-0.8126)

3. $\begin{aligned} \arctan (- 1.9249) \end{aligned}$
::3. arctan(-1.9249)

Examples
::实例

Example 1
::例1

Earlier, you were asked to evaluate $\begin{aligned} \sec^{- 1} \frac{2}{\sqrt{3}} \end{aligned}$
::早些时候,你被要求评估秒-123

You can start with the inverse reciprocal property:
::您可以从反对等财产开始:

$\begin{aligned} \sec^{- 1} x = \cos^{- 1} \frac{1}{x} \end{aligned}$
::秒- 1x=cos- 11x

Substituting in values for "x" gives:
::替换“ x” 给付的值 :

$\begin{aligned} \sec^{- 1} \frac{2}{\sqrt{3}} = \cos^{- 1} \frac{1}{\frac{2}{\sqrt{3}}} \end{aligned}$
::-123=cos-1123

This can be rewritten as:
::可以重写为:

$\begin{aligned} \cos^{- 1} \frac{\sqrt{3}}{2} \end{aligned}$
::COS-132

And
::还有

$\begin{aligned} \cos^{- 1} \frac{\sqrt{3}}{2} = \frac{π}{6} \end{aligned}$
::COS - 1 3 6

Therefore,
::因此,

$\begin{aligned} \sec^{- 1} \frac{2}{\sqrt{3}} = \frac{π}{6} \end{aligned}$
::仅次于 1 23 6

Example 2
::例2

Evaluate $\begin{aligned} \sec^{- 1} (- 2) \end{aligned}$
::评价秒-1(-2)

$\begin{aligned} \frac{2 π}{3} \end{aligned}$

Example 3
::例3

Evaluate $\begin{aligned} \cot^{- 1} (- 1) \end{aligned}$
::评价(-1)

$\begin{aligned} - \frac{π}{4} \end{aligned}$

Example 4
::例4

Evaluate $\begin{aligned} \csc^{- 1} (\sqrt{2}) \end{aligned}$
::评价csc-1(2)

$\begin{aligned} \frac{π}{4} \end{aligned}$

Review
::回顾

Using technology, find the value in radian measure, of each of the following.
::使用技术,找到以下每种光度的弧度值。

$\begin{aligned} \sin^{- 1} (.345) \end{aligned}$
:345) (一)-(一)-(一)-(一)-(一)-(一)-(三)-(三)

$\begin{aligned} \cos^{- 1} (.87) \end{aligned}$
:.87) (c)-(c)-(c)-(c)

$\begin{aligned} \csc^{- 1} (4) \end{aligned}$
::csc-1(4)

$\begin{aligned} \sec^{- 1} (2.32) \end{aligned}$
::秒-1(2.32)

$\begin{aligned} \cot^{- 1} (5.2) \end{aligned}$
::COt-1(5.2)

Find the exact value of each expression within the restricted domain, without a calculator.
::在限制域内查找每个表达式的准确值,不使用计算器。

$\begin{aligned} \sec^{- 1} (\frac{2 \sqrt{3}}{3}) \end{aligned}$
:233) (233)

$\begin{aligned} \csc^{- 1} (1) \end{aligned}$
::csc-1_________(1)

$\begin{aligned} \cot^{- 1} (\sqrt{3}) \end{aligned}$
::COt-1-1(3)

$\begin{aligned} \csc^{- 1} (2) \end{aligned}$
::csc-1_________________(2)

$\begin{aligned} \sec^{- 1} (\sqrt{2}) \end{aligned}$
::空间-1(2)

$\begin{aligned} \cot^{- 1} (1) \end{aligned}$
::COT-1-1_______(1)

$\begin{aligned} \cos^{- 1} (\frac{1}{2}) \end{aligned}$
::COS-1( 12)

$\begin{aligned} \sec^{- 1} (2) \end{aligned}$
::空间-1(2)

$\begin{aligned} \cot^{- 1} (\frac{\sqrt{3}}{3}) \end{aligned}$
:33)

$\begin{aligned} \sin^{- 1} (\frac{\sqrt{3}}{2}) \end{aligned}$
:32)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

反对等三角函数的定义

Inverse Reciprocal Trigonometric Functions ::反对等三角函数

Finding the Inverse ::查找反向

Finding the Exact Value ::查找精确值

Using Technology ::使用技术

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Inverse Reciprocal Trigonometric Functions
::反对等三角函数

Finding the Inverse
::查找反向

Finding the Exact Value
::查找精确值

Using Technology
::使用技术

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)