4.9 代数术语中的三角计量法

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节代数术语中的三角测量法

  折叠 展开

  代数术语中的三角测量法

  播放段落

  You are babysitting your little cousin while doing your homework. While working on your trig functions, your cousin asks you what you are doing. While trying to explain sine, cosine, and tangent, your cousin is very confused. She doesn't understand what you mean by those words, but really wants to understand what the functions mean. Can you define the trig functions in terms of the relationships of sides for your little cousin?
  ::你在做功课时照看你的小表弟。在做功课时,你的表弟问你在做什么。在解释正弦、顺弦和正弦时,你的表弟非常困惑。她不明白你所说的这些话是什么意思,但真的想知道这些功能意味着什么。你能用你小表弟的两面关系来定义三角函数吗?

  播放段落

  Solving Trigonometric Functions
  ::解决三角函数

  播放段落

  All of the trigonometric functions can be rewritten in terms of only $\begin{array}{r}x\end{array}$ , when using one of the inverse trigonometric functions.
  ::当使用反三角函数之一时,所有三角函数只能用 x 重写。

  播放段落

  Starting with tangent, we draw a triangle where the opposite side (from $\begin{array}{r}\theta \end{array}$ ) is defined as $\begin{array}{r}x\end{array}$ and the adjacent side is 1. The hypotenuse, from the would be $\begin{array}{r}\sqrt{x^2+1}\end{array}$ . Substituting $\begin{array}{r}{\tan }^{-1}x\end{array}$ for $\begin{array}{r}\theta \end{array}$ , we get:
  ::从正切开始, 我们绘制一个三角形, 将对立面( 从 __ ) 定义为 x , 相邻侧为 1 。 下限为 x2+1 。 替代 tan - 1 x , 我们得到 :

  

  播放段落

  $$\begin{array}{rl}\tan \theta & =\frac{x}{1}\\ \tan \theta & =x& & hypotenuse=\sqrt{x^2+1}\\ \theta & ={\tan }^{-1}x\end{array}$$

  
  ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

  播放段落

  $$\begin{array}{rlrl}\sin ({\tan }^{-1}x)& =\sin \theta =\frac{x}{\sqrt{x^2+1}}& & \csc ({\tan }^{-1}x)=\csc \theta =\frac{\sqrt{x^2+1}}{x}\\ \cos ({\tan }^{-1}x)& =\cos \theta =\frac{1}{\sqrt{x^2+1}}& & \sec ({\tan }^{-1}x)=\sec \theta =\sqrt{x^2+1}\\ \tan ({\tan }^{-1}x)& =\tan \theta =x& & \cot ({\tan }^{-1}x)=\cot \theta =\frac{1}{x}\end{array}$$

  
  :tan-1x) =sinxx2+1csc(tan-1x) =cscx2+1xcos *(tan-1x) =cos1x2+1sec}(tan-1x) =secx2+1tan(tan-1x) =tanxcot(tan-1x) =cot1xx

  播放段落

  Simplifying Trigonometric Functions
  ::简化三角函数

  播放段落

  1. Find $\begin{array}{r}\sin ({\tan }^{-1}3x)\end{array}$ .
  ::1. 找出sin(tan-13x)。

  播放段落

  Instead of using $\begin{array}{r}x\end{array}$ in the ratios above, use $\begin{array}{r}3x\end{array}$ .
  ::在上述比率中使用x,而不是使用x,使用3x。

  播放段落

  $$\begin{array}{r}\sin ({\tan }^{-1}3x)=\sin \theta =\frac{3x}{\sqrt{(3x{)}^2+1}}=\frac{3x}{\sqrt{9x^2+1}}\end{array}$$

  
  :tan- 1 @% 3x) =sin @ 3x( 3x) 2+1=3x9x2+1

  播放段落

  2. Find $\begin{array}{r}{\sec }^2({\tan }^{-1}x)\end{array}$ .
  ::2. 查找 sec2(tan-1x)。

  播放段落

  This problem might be better written as $\begin{array}{r}[\sec ({\tan }^{-1}x){]}^2\end{array}$ . Therefore, all you need to do is square the ratio above.
  ::这个问题最好写成[sec(tan-1x)]2。 因此,你需要做的只是以上比例的平方。

  播放段落

  $$\begin{array}{r}[\sec ({\tan }^{-1}x){]}^2={\left(\sqrt{x^2+1}\right)}^2=x^2+1\end{array}$$

  
  ::[sec( tan- 1x)] 2= (x2+1) 2=x2+1) 2=x2+1

  播放段落

  You can also write the all of the trig functions in terms of arcsine and arccosine. However, for each inverse function , there is a different triangle. You will derive these formulas in the exercise for this section.
  ::您也可以用弧素和弧cosine 来写入所有三角函数。但是,对于每个反函数,则有一个不同的三角形。您可以在为本节的练习中得出这些公式。

  播放段落

  3. Find $\begin{array}{r}{\csc }^3({\tan }^{-1}4x)\end{array}$ .
  ::3. 查找 csc3(tan-14x)。

  播放段落

  This problem is similar to #1 and #2 above. First, use $\begin{array}{r}4x\end{array}$ instead of $\begin{array}{r}x\end{array}$ in the ratios above. Second, the $\begin{array}{r}{\csc }^3\end{array}$ is the same as taking the $\begin{array}{r}\csc \end{array}$ function and cubing it.
  ::这个问题与上面的#1和#2相似。 首先, 使用 4x 而不是 x 在上面的比重中 。 其次, csc3 与 采取 csc 函数并进行缩放相同 。

  播放段落

  $$\begin{array}{r}[\csc ({\tan }^{-1}4x){]}^3={\left(\frac{\sqrt{(4x{)}^2+1}}{4x}\right)}^3=\frac{(16x^2+1{)}^{3/2}}{64x^3}\end{array}$$

  
  ::[csc( tan- 14x)] 3=( (4x) 2+14x) 3=( 16x2+1) 3/264x3

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked if you can define the trig functions in terms of the relationship of sides. 
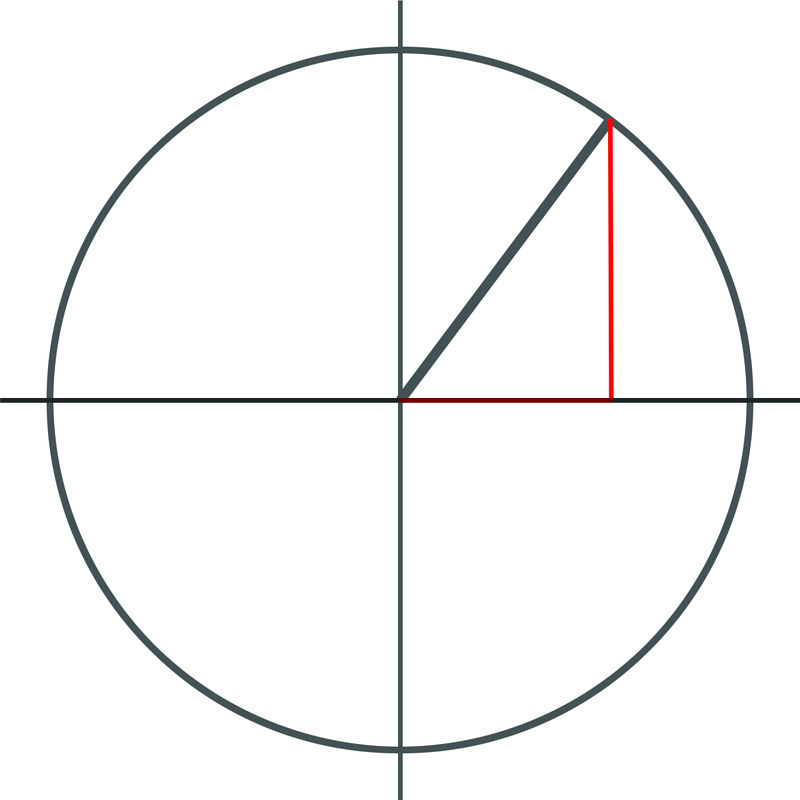
  ::早些时候,有人问您是否可以从双方关系的角度界定三角函数。

  播放段落

  As it turns out, it's very easy to explain trig functions in terms of ratios. If you look at the unit circle
  ::事实证明,以比率来解释三角形函数很容易。如果你看看单位圆

  

  播放段落

  you can see that each trig function can be represented as a ratio of two sides. The value of any trig function can be represented as the length of one of the sides of the triangle (shown with two red sides and the black hypotenuse) divided by the length of one of the other sides. In fact, you should explain to your cousin, the words like "sine", "cosine", and "tangent" are just conveniences in this case to describe relationships that keep coming up over and over again. It would be possible to just describe the trig functions in terms of relationships of one side to another, if you'd like.
  ::您可以看到, 每个三角函数都可以作为两边之比来表示。 任何三角函数的价值都可以作为三角形两边的长度来表示( 以红色两面和黑色下限显示) 。 事实上, 您应该向您的表兄解释“ sine”、“ cosine” 和“ tangent” 等字眼, 以描述不断出现的关系。 如果您愿意的话, 可以只描述一面关系中的三角函数 。

  播放段落

  Using the sides of a triangle made on the unit circle, if the side opposite the angle is called "x":
  ::使用单位圆上三角形的侧面,如果角度对面的侧面称为“x”:

  播放段落

  $$\begin{array}{r}\sin =\frac{opposite}{hypotenuse}=\frac{x}{\sqrt{x^2+1}}\\ \cos =\frac{adjacent}{hypotenuse}=\frac{1}{\sqrt{x^2+1}}\\ \tan =\frac{opposite}{adjacent}=\frac{x}{1}\end{array}$$

  
  ::近地点日光生物=1x2+1cos=近地点日光生物=1x2+1tan=对面日光生物=1x1

  播放段落

  So as you can see, since trig functions are really just relationships between sides, it is possible to work with them in whatever form you want; either in terms of the usual "sine", "cosine" and "tangent", or in terms of algebra.
  ::如你所见, 因为三角函数其实只是两边的关系, 可以用任何你想要的形式与他们合作; 或者用通常的“sine”、“cosine”和“cangrent”来表达, 或者用代数来表达。

  播放段落

  Example 2
  ::例2

  播放段落

  Express $\begin{array}{r}{\cos }^2({\tan }^{-1}x)\end{array}$ as an algebraic expression involving no trigonometric functions.
  ::Express cos2(tan-1x)作为代数表达式,无三角函数。

  播放段落

  $\begin{array}{r}\frac{1}{x^2+1}\end{array}$
  ::1x2+1

  播放段落

  Example 3
  ::例3

  播放段落

  Express $\begin{array}{r}\cot ({\tan }^{-1}{x}^2)\end{array}$ as an algebraic expression involving no trigonometric functions.
  ::Express cot(tan-1x2)作为代数表达式,无三角函数。

  播放段落

  $\begin{array}{r}\frac{1}{x^2}\end{array}$
  ::1x2

  播放段落

  Example 4
  ::例4

  播放段落

  To find trigonometric functions in terms of sine inverse, use the following triangle.
  ::要以正弦反函数查找三角函数,请使用以下三角形。

  

  播放段落

  Determine the sine, cosine and tangent in terms of arcsine. Find $\begin{array}{r}\tan ({\sin }^{-1}2x^3)\end{array}$ .
  ::确定正弦、 共弦和正切值, 以弧相为单位。 查找 tan( sin_ 1)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  The adjacent side to $\begin{array}{r}\theta \end{array}$ is $\begin{array}{r}\sqrt{1-x^2}\end{array}$ , so the three trig functions are:
  ::的邻接侧是1-x2, 所以三个三角函数是:

  播放段落

  $$\begin{array}{rl}\sin ({\sin }^{-1}x)& =\sin \theta =x\\ \cos ({\sin }^{-1}x)& =\cos \theta =\sqrt{1-x^2}\\ \tan ({\sin }^{-1}x)& =\tan \theta =\frac{x}{\sqrt{1-x^2}}\end{array}$$

  $$\begin{array}{r}\tan ({\sin }^{-1}(2x^3))=\frac{2x^3}{\sqrt{1-(2x^3{)}^2}}=\frac{2x^3}{\sqrt{1-4x^6}}\end{array}$$

  
  ::=2x31 -(2x3)2=2x31 -(2x3)2=2x31 -(2x3)2=2x31 -4x6

  播放段落

  Review
  ::回顾

  播放段落

  Rewrite each expression as an algebraic expression involving no trigonometric functions.
  ::将每个表达式重写为代数表达式,不包含三角函数。

  播放段落
  1. $\begin{array}{r}\sin ({\tan }^{-1}5x)\end{array}$
     ::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:
  播放段落
  2. $\begin{array}{r}\cos ({\tan }^{-1}2x^2)\end{array}$
     ::COs( tan- 12x2)
  播放段落
  3. $\begin{array}{r}\cot ({\tan }^{-1}3x^2)\end{array}$
     ::comt( tan- 13x2)
  播放段落
  4. $\begin{array}{r}\sin ({\cos }^{-1}x)\end{array}$
     :cos- 1x) (cos- 1x)
  播放段落
  5. $\begin{array}{r}\sin ({\cos }^{-1}3x)\end{array}$
     :cos- 13x)
  播放段落
  6. $\begin{array}{r}\cos ({\sin }^{-1}2x^2)\end{array}$
     ::COs( 辛- 12x2)
  播放段落
  7. $\begin{array}{r}\csc ({\cos }^{-1}x)\end{array}$
     ::csc(cos- 1x)
  播放段落
  8. $\begin{array}{r}\sec ({\sin }^{-1}x)\end{array}$
     ::秒( 辛- 1x)
  播放段落
  9. $\begin{array}{r}{\cos }^2({\tan }^{-1}3x^2)\end{array}$
     ::COs2( tan- 13x2)
  播放段落
  10. $\begin{array}{r}\sin ({\sec }^{-1}x)\end{array}$
      :sec-1x)
  播放段落
  11. $\begin{array}{r}\cos ({\csc }^{-1}x)\end{array}$
      ::COs(csc- 1x)
  播放段落
  12. $\begin{array}{r}\sin ({\tan }^{-1}2x^3)\end{array}$
      ::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:
  播放段落
  13. $\begin{array}{r}\cos ({\sin }^{-1}3x)\end{array}$
      ::COs( 辛- 1% 3x)
  播放段落
  14. $\begin{array}{r}\sin ({\sec }^{-1}x)\end{array}$
      :sec-1x)
  播放段落
  15. $\begin{array}{r}\cos ({\cot }^{-1}x)\end{array}$
      ::cos( cot- 1 x)

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。