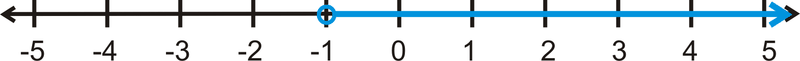1.10 解决基本不平等

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 解决基本不平等

  Collapse Expand

  解决基本不平等

  播放段落

  The average weight gain of an infant, after 6 months of age, is one pound a month, until the age of 2. If the average 6-month-old weighs 16 pounds, up to what age would an infant weigh 25 pounds or less?
  ::婴儿在6个月后,平均体重增加是每月一磅,直到2岁。 如果6个月的平均体重为16磅,则婴儿的体重为25磅或不足25磅到什么年龄?

  播放段落

  Basic Inequalities
  ::基本不平等

  播放段落

  Solving a linear inequality is very similar to solving a linear equality, or equation . There are a few very important differences. We no longer use an equal sign. There are four different inequality signs , shown below.
  ::解决线性不平等与解决线性平等或等式非常相似。 有一些非常重要的区别。 我们不再使用平等标志。 下面显示四个不同的不平等迹象。

  播放段落

  $\begin{align*} < \end{align*}$ Less than
  ::<小于

  播放段落

  $\begin{align*} > \end{align*}$ Greater than
  ::> 大于

  播放段落

  $\begin{align*} \le \end{align*}$ Less than or equal to
  ::小于或等于

  播放段落

  $\begin{align*} \ge \end{align*}$ Greater than or equal to
  ::大于或等于

  播放段落

  Notice that the line underneath the $\begin{align*}\le\end{align*}$ and $\begin{align*}\ge\end{align*}$ signs indicates “equal to.” The inequality $\begin{align*}x>-1\end{align*}$ would be read, “ $\begin{align*}x\end{align*}$ is greater than -1.” We can also graph these solutions on a number line. To graph an inequality on a number line, shading is used. This is because an inequality is a range of solutions, not just one specific number. To graph $\begin{align*}x>-1\end{align*}$ , it would look like this:
  ::请注意 和 符号下方的直线表示“ 相等 ” 。 不平等 x 1 将读为 , “ x 大于 - 1 ” 。 我们也可以用数字线绘制这些解决方案。 要用数字线绘制不平等图, 则使用阴影。 这是因为不平等是一系列解决方案, 而不仅仅是一个特定数字。 图 x 1 将看起来是这样 :

  

  播放段落

  Notice that the circle at -1 is open . This is to indicate that -1 is not included in the solution. A < sign would also have an open circle. If the inequality was a $\begin{align*}\ge\end{align*}$ or $\begin{align*}\le\end{align*}$ sign, then the circle would be closed, or filled in. Shading to the right of the circle shows that any number greater than -1 will be a solution to this inequality.
  ::注意 - 1 的圆是打开的。 这是表示 - 1 不包含在解决方案中 。 < 符号也会有一个开放的圆 。 如果不平等是一个 + 或 + 的符号, 那么圆将被关闭或填满 。 将圆向右方的形状显示, 任何大于 - 1 的数值都将是解决这一不平等的办法 。

  播放段落

  Let's determine whether  $\begin{align*}x=-8\end{align*}$  is a solution to $\begin{align*}\frac{1}{2}x+6>3\end{align*}$ .
  ::让我们确定 x8 是否是 12x+6> 3 的解决方案 。

  播放段落

  Plug in -8 for $\begin{align*}x\end{align*}$ and test this solution.
  ::x 的 - 8 插件并测试此溶液 。

  $$\begin{align*}\frac{1}{2}(-8)+6 &> 3\\ -4+6 &> 3\\ 2 &> 3\end{align*}$$

  播放段落

  Of course, 2 cannot be greater than 3. Therefore , this is not a valid solution.
  ::当然,2个不能大于3个,因此,这不是一个有效的解决办法。

  播放段落

  Now, let's solve the following basic inequalities.
  ::现在,让我们解决以下基本的不平等问题。

  播放段落
  1. Solve and graph the solution to $\begin{align*}2x-5 \le 17\end{align*}$ .
     ::解析并绘制2x-517的解决方案图。

  播放段落

  For the most part, solving an inequality is the same as solving an equation. The major difference will be addressed in problem #2 below. This inequality can be solved just like an equation.
  ::大部分情况下,解决不平等与解决等式是一样的。 主要的差别将在下面问题2中解决。 这种不平等可以像解决等式一样解决。

  播放段落

  $$\begin{align*}& 2x-\bcancel{5} \le 17\\ & \underline{\quad \ + \bcancel{5} \ +5 \; \;}\\ & \quad \ \frac{\bcancel{2}x}{\bcancel{2}} \le \frac{22}{2}\\ & \qquad x \le 2\end{align*}$$
  ::2x-517+5+5+5_2x2__222x__2

  播放段落

  Test a solution, $\begin{align*}x = 0: 2(0)-5 \le 17 \rightarrow -5 \le 17 \checkmark\end{align*}$
  ::测试溶液, x=0: 2(0) - 517=51717________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Plotting the solution, we get:
  ::设计解决方案,我们得到:

  

  播放段落

  Always test a solution that is in the solution range. It will help you determine if you solved the problem correctly.
  ::总是在解决方案范围内测试一个解决方案。 它会帮助您确定您是否正确解决了问题 。

  播放段落
  2. Solve and graph $\begin{align*}-6x+7 \le - 29\end{align*}$ .
     ::解析和图表 - 6x+7\\\\\\\29。

  播放段落

  When solving inequalities, be careful with negatives. Let’s solve this problem the way we normally would an equation.
  ::在解决不平等问题时,要小心负面因素。 让我们以我们通常的等式来解决这个问题。

  播放段落

  $$\begin{align*}& -6x+\bcancel{7} \le -29\\ & \underline{\qquad \ \ -\bcancel{7} \quad \ -7 \; \; \; \;}\\ & \qquad \frac{-\bcancel{6}x}{-\bcancel{6}x} \le \frac{-36}{-6}\\ & \qquad \quad \ x \le 6\end{align*}$$
  ::-6x+729 -7 -7*6x6x6*36 -6x6*6

  播放段落

  Let’s check a solution. If $\begin{align*}x\end{align*}$ is less than or equal to 6, let’s test 1.
  ::让我们检查一个解决方案。 如果 x 小于或等于 6, 让我们测试 1 。

  $$\begin{align*}-6(1)+7 & \le -29\\ -6+7 & \le -29\\ 1 & \bcancel{\le} -29\end{align*}$$

  播放段落

  This is not a true inequality. To make this true, we must flip the inequality. Therefore, whenever we multiply or divide by a negative number, we must flip the inequality sign. The answer to this inequality is actually $\begin{align*}x\ge 6\end{align*}$ . Now, let’s test a number in this range.
  ::这不是真正的不平等。 要做到这一点,我们必须翻转不平等。 因此,每当我们以负数乘以或除以负数时,我们必须翻转不平等标志。 这种不平等的答案其实是x6。 现在,让我们在这个范围内测试一个数字。

  $$\begin{align*}-6(10)+7 & \le - 29\\ -60+7 & \le -29\\ -60 & \le -29\end{align*}$$

  播放段落

  This is true. The graph of the solution is:
  ::这就是事实。解决方案的图示是:

  

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find the last age (the maximum age) that an infant would weigh 25 pounds or less.
  ::早些时候,有人要求你找到婴儿的最后一个年龄(最大年龄),即体重25磅或不足25磅。

  播放段落

  First, write an inequality. Let m represent the age of the infant, in months. Remember, when you get the final answer, you must add 6 for the initial weight of the infant at 6 months.
  ::首先,写一个不平等的字。让 m 代表婴儿的年龄, 在几个月内。 记住, 当得到最后答案时, 6个月时, 婴儿的初始体重必须增加 6 个 。

  播放段落

  $$\begin{align*}16 + m \le 25 \\ m \le 9 \end{align*}$$
  ::16+m%25m%9

  播放段落

  Adding 6, we have $\begin{align*}m \le 15\end{align*}$ . So, up to 15 months, the average baby should weigh 25 pounds or less.
  ::最多15个月,平均婴儿体重应该25磅或不足25磅。

  播放段落

  Example 2
  ::例2

  播放段落

  Is $\begin{align*}x = -5\end{align*}$ a solution to $\begin{align*}-3x+7>12\end{align*}$ ?
  ::x*% 5 是- 3x+7> 12 的解决方案吗 ?

  播放段落

  Plug -5 into the inequality.
  ::将5分插在不平等中。

  $$\begin{align*}-3(-5)+7 &>12\\ 15+7&>12\end{align*}$$

  播放段落

  This is true because 22 is larger than 12. -5 is a solution.
  ::这是正确的,因为22大于12 -5是一个解决办法。

  播放段落

  Example 3
  ::例3

  播放段落

  Solve and graph the solution to  $\begin{align*}\frac{3}{8}x+5<26\end{align*}$ .
  ::解析和图形显示 38x+5 < 26 的解决方案 。

  播放段落

  No negatives with the $\begin{align*}x-\end{align*}$ term , so we can solve this inequality like an equation.
  ::在x- term上没有负值, 所以我们可以像方程式一样解决这种不平等。

  播放段落

  $$\begin{align*}& \frac{3}{8}x+\bcancel{5}<26\\ & \underline{\quad \ -\bcancel{5} \ \ -5 \; \; \; \; \; \;}\\ & \ \xcancel{\frac{8}{3} \cdot \frac{3}{8}}x<21 \cdot \frac{8}{3}\\ & \qquad \ x<56\end{align*}$$
  ::38x+5 < 5x5 < 26 - 5 - 5_ 83_ 38x < 21883x < 56

  播放段落

  Test a solution, $\begin{align*}x = 16: \frac{3}{8}(16)+5 < 26 \checkmark\end{align*}$
  ::测试溶液, x=16:38(16)+5<26

  $\begin{align*}6+5 < 26\end{align*}$

  播放段落

  The graph looks like:
  ::图表看起来像:

  

  播放段落

  Example 4
  ::例4

  播放段落

  Solve and graph the solution to  $\begin{align*}11<4-x\end{align*}$ .
  ::将解决方案解析和图形到 11 < 4- x 。

  播放段落

  In this inequality, we have a negative $\begin{align*}x-\end{align*}$ term. Therefore, we will need to flip the inequality.
  ::在这种不平等中,我们有一个消极的x-条件,因此,我们需要扭转这种不平等。

  播放段落

  $$\begin{align*}& \ \ 11<\bcancel{4}-x\\ & \underline{-4 \ \ - \bcancel{4} \; \; \; \; \; \; \;}\\ & \frac{7}{-1} < \frac{\bcancel{-}x}{\bcancel{-1}}\\ & -7>x\end{align*}$$
  ::11 < 4 - x - 4 - 4 - 4_ 7 - 1 - 1 - 1 - 1 - 7 > x

  播放段落

  Test a solution, $\begin{align*}x = -10: 11 < 4-(-10) \checkmark\end{align*}$
  ::测试溶液, x10:11<4-(-)___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  $\begin{align*}11 < 14\end{align*}$

  播放段落

  Notice that we flipped  the inequality sign when we divided  by -1. Also, this equation can also be written $\begin{align*}x< -7\end{align*}$ .
  ::注意当我们除以 -1. 时我们翻转了不平等符号。 另外, 这个方程式也可以写成 x @ @ @ 7 。

  播放段落

  Here is the graph:
  ::以下是图表:

  

  播放段落

  Review
  ::回顾

  播放段落

  Solve each inequality.
  ::解决每一种不平等。

  播放段落
  1. $\begin{align*}x+5>-6\end{align*}$
     ::x+56
  播放段落
  2. $\begin{align*}2x \ge 14\end{align*}$
     ::2x14
  播放段落
  3. $\begin{align*}4<-x\end{align*}$
     ::4x
  播放段落
  4. $\begin{align*}3x-4 \le 8\end{align*}$
     ::3x-48
  播放段落
  5. $\begin{align*}21-8x<45\end{align*}$
     ::21-8x<45
  播放段落
  6. $\begin{align*}9>x-2\end{align*}$
     ::9>x-2
  播放段落
  7. $\begin{align*}\frac{1}{2}x+5 \ge 12\end{align*}$
     ::12x+5=12
  播放段落
  8. $\begin{align*}54 \le -9x\end{align*}$
     ::549x
  播放段落
  9. $\begin{align*}-7<8+\frac{5}{6}x\end{align*}$
     ::-7<8+56x
  播放段落
  10. $\begin{align*}10-\frac{3}{4}x<-8\end{align*}$
      ::10-34x8
  播放段落
  11. $\begin{align*}4x+15 \ge 47\end{align*}$
      ::4x+15447
  播放段落
  12. $\begin{align*}0.6x-2.4<4.8\end{align*}$
      ::0.6x-2.4 < 4.8
  播放段落
  13. $\begin{align*}1.5>-2.7-0.3x\end{align*}$
      ::1.52.7-0.3x
  播放段落
  14. $\begin{align*}-11<12x+121\end{align*}$
      ::- 11 < 12x+121
  播放段落
  15. $\begin{align*}\frac{1}{2}-\frac{3}{4}x \le -\frac{5}{8}\end{align*}$
      ::12-34x58

  播放段落

  For questions 16 and 17, write the inequality statement given by the graph below.
  ::对于问题16和17,请写下图提供的不平等情况说明。

  16. 
  17. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。