5.2 利用科士氏定律确定未知角

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节使用科信定律确定未知角度

  折叠 展开

  使用科信定律确定未知角度

  播放段落

  You and a group of your friends are out in the country playing paintball. You have a playing field that is a triangle with sides of 50 meters, 50 meters, and 80 meters. You're trying to figure out what the angle is between the side that has a length of 50 meters and the other side that has a length of 50 meters. Is there a way to do this?
  ::你和一群朋友在这个国家玩彩弹。 你们有一个三角形的游戏场, 边边50米, 边50米, 边80米。 你们想弄清楚, 边50米, 边50米, 边50米, 边50米, 边50米, 边50米, 边50米, 边50米, 边50米, 边50米, 边50米之间的角。 有没有办法?

  播放段落

  Using Law of Cosines to Find Unknown Angles
  ::使用 Cosines 定律查找未知角度

  播放段落

  The is a natural extension of the that allows us to perform calculations to find the sides of triangles that are oblique.
  ::这是自然延伸 使我们能够进行计算 找到斜斜的三角形的侧面

  播放段落

  Remember that the Law of Cosines is a generalization of the Pythagorean Theorem, where the angle $\begin{array}{r}C\end{array}$ is the angle between the two given sides of a triangle:
  ::记住,《科辛斯定律》是毕达哥里安神话的概括,其角度C是三角形两侧之间的角:

  播放段落

  $\begin{array}{r}{c}^2=a^2+b^2-2(a)(b)\cos C\end{array}$
  ::c2=a2+b2-2(a)(b)cosC

  播放段落

  You'll notice that if this were a right triangle, $\begin{array}{r}\cos C=\cos {90}^{\circ }=0\end{array}$ , and so the third term would disappear, leaving the familiar Pythagorean Theorem.
  ::你会注意到,如果这是一个正确的三角形, cosC=cosC900, 所以第三学期就会消失, 留下熟悉的毕达哥伦神话。

  播放段落

  Another situation where we can apply the Law of Cosines is when we know all three sides in a triangle (SSS) and we need to find one of the angles. The Law of Cosines allows us to find any of the three angles in the triangle. First, we will look at how to apply the Law of Cosines in this case, and then we will look at the real-world application given in the problem above.
  ::我们可以适用《科辛斯定律》的另一个情况是,我们了解三角形中的所有三面,我们需要找到一个角度。《科辛斯定律》允许我们在三角形中找到任何三个角度。首先,我们将研究在这种情况下如何适用科辛斯定律,然后我们将研究上述问题中真实世界的应用。

  播放段落

  Using the Law of Cosines 
  ::使用科斯定律

  播放段落

  For the following problems, solve using the Law of Cosines. 
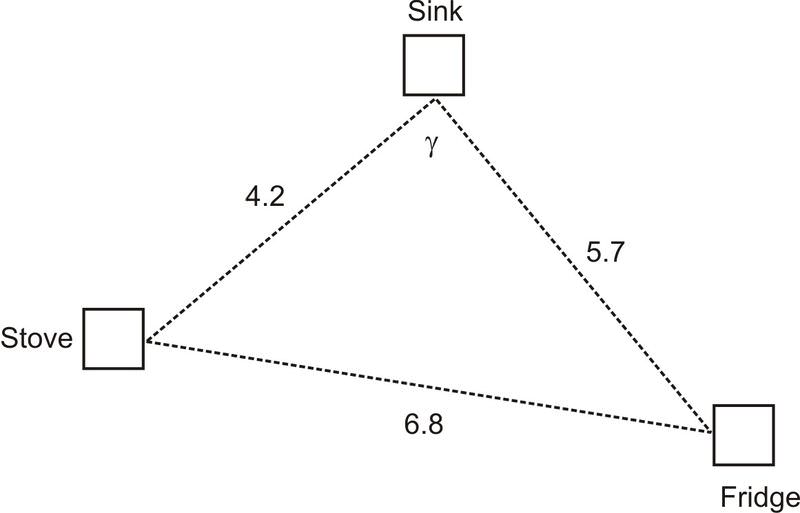
  ::对于以下的问题,使用《科辛斯定律》解决。

  播放段落

  1. An architect is designing a kitchen for a client. When designing a kitchen, the architect must pay special attention to the placement of the stove, sink, and refrigerator. In order for a kitchen to be utilized effectively, these three amenities must form a triangle with each other. This is known as the “work triangle.” By design, the three parts of the work triangle must be no less than 3 feet apart and no more than 7 feet apart . Based on the dimensions of the current kitchen, the architect has determined that the sink will be 3.6 feet away from the stove and 5.7 feet away from the refrigerator. The sink forms a $\begin{array}{r}{103}^{\circ }\end{array}$ angle with the stove and the refrigerator. If the architect moves the stove so that it is 4.2 feet from the sink and makes the fridge 6.8 feet from the stove, how does this affect the angle the sink forms with the stove and the refrigerator?
  ::1. 建筑师为客户设计厨房:设计厨房时,建筑师必须特别注意炉子、水槽和冰箱的布置;为使厨房得到有效利用,这三种设施必须形成三角形,称为 " 工作三角形 " 。设计时,工作三角形的三个部分必须不少于3英尺,距离不超过7英尺。根据目前厨房的尺寸,建筑师确定水槽离炉子有3.6英尺,离冰箱有5.7英尺。水槽与炉子和冰箱有103角。如果建筑师将炉子从水槽挪开4.2英尺,使冰箱从炉子取6.8英尺,这如何影响水槽与炉子和冰箱的角?

  

  播放段落

  In order to find how the angle is affected, we will again need to use the Law of Cosines, but because we do not know the measures of any of the angles, we solve for $\begin{array}{r}Y\end{array}$ .
  ::为了找出角度是如何受到影响的, 我们再次需要使用 科辛斯定律, 但是因为我们不知道 任何角度的量度, 我们解决Y。

  播放段落

  $$\begin{array}{rlrl}{6.8}^2& ={4.2}^2+{5.7}^2-2(4.2)(5.7)\cos Y& & \text{Law of Cosines}\\ 46.24& =17.64+32.49-2(4.2)(5.7)\cos Y& & \text{Simplify squares}\\ 46.24& =17.64+32.49-47.88\cos Y& & \text{Multiply}\\ 46.24& =50.13-47.88\cos Y& & \text{Add}\\ -3.89& =-47.88\cos Y& & \text{Subtract}\\ 0.0812447786& =\cos Y& & \text{Divide}\\ {85.3}^{\circ }& \approx Y& & {\cos }^{-1}(0.081244786)\end{array}$$

  
  ::6.82=4.22+5.72-2(4.2)(5.7)cos < 科辛斯法律46.24=17.64+32.49-2(4.2)(5.7)cos_简化正方形46.24=17.64+32.49-47.88cos_YUltiply46.24=50.1347-88cos*YAdd-3.8947.88cos_YSubtreal0.081447786=CosçYDivide85.3_Ycos-1}(0.081244786)

  播放段落

  The new angle would be $\begin{array}{r}{85.3}^{\circ }\end{array}$ , which means it would be $\begin{array}{r}{17.7}^{\circ }\end{array}$ less than the original angle.
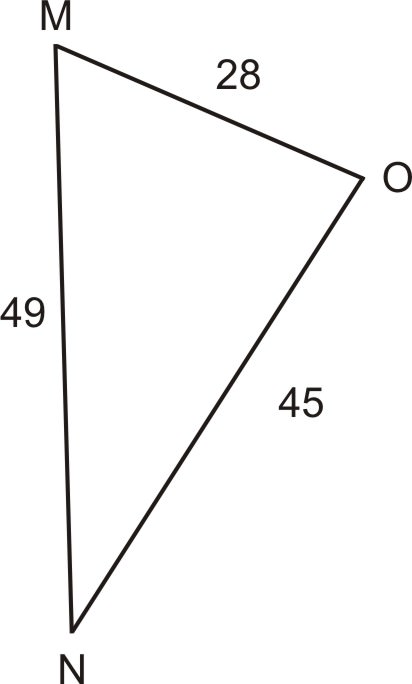
  ::新的角度将是85.3,这意味着比原来的角度少17.7。

  播放段落

  2. In oblique $\begin{array}{r}\mathrm{△}MNO,m=45,n=28\end{array}$ , and $\begin{array}{r}o=49\end{array}$ . Find $\begin{array}{r}\mathrm{\angle }M\end{array}$ .
  ::2. 在斜体中,m=45,n=28,o=49。

  

  播放段落

  Since we know all three sides of the triangle, we can use the Law of Cosines to find $\begin{array}{r}\mathrm{\angle }M\end{array}$ .
  ::既然我们知道三角形的三边, 我们可以用科辛斯定律来找到ZM。

  播放段落

  $$\begin{array}{rlrl}{45}^2& ={28}^2+{49}^2-2(28)(49)\cos M& & \text{Law of Cosines}\\ 2025& =784+2401-2(28)(49)\cos M& & \text{Simplify squares}\\ 2025& =784+2401-2744\cos M& & \text{Multiply}\\ 2025& =3185-2744\cos M& & \text{Add}\\ -1160& =-2744\cos M& & \text{Subtract}3185\\ 0.422740525& =\cos M& & \text{Divide by}-2744\\ {65}^{\circ }& \approx M& & {\cos }^{-1}(0.422740525)\end{array}$$

  
  ::452=282+492-2(28)(49cos=CosinesMLLaw2025=784+2401-2(28)(49cos=简化正方2025=784+2401-27444cosMMMultiply2025=3185-2744cosMAdd-11602744cos*MSubtrapt 31850.422740525=cosMdivide by-274465Mcos-1(0.422740525)

  播放段落

  It is important to note that we could use the Law of Cosines to find $\begin{array}{r}\mathrm{\angle }N\end{array}$ or $\begin{array}{r}\mathrm{\angle }O\end{array}$ also.
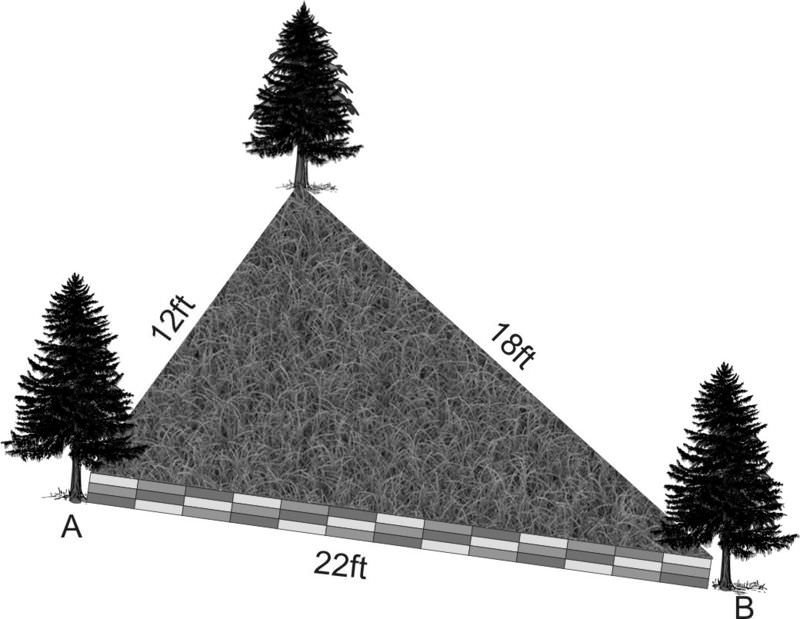
  ::需要指出的是,我们可以利用《科辛斯定律》来找到“N”或“O”。

  播放段落

  3. Sam is building a retaining wall for a garden that he plans on putting in the back corner of his yard. Due to the placement of some trees, the dimensions of his wall need to be as follows: side $\begin{array}{r}1=12ft\end{array}$ , side $\begin{array}{r}2=18ft\end{array}$ , and side $\begin{array}{r}3=22ft\end{array}$ . At what angle do side 1 and side 2 need to be? Side 2 and side 3? Side 1 and side 3?
  ::3. Sam正在为他计划放置在院子后角的花园建造一座保留墙,由于设置了一些树木,其墙的尺寸必须如下:1=12ft,2=18ft,3=22ft。1和2侧需要什么角度?2和3?1和3侧?3和3侧?

  

  播放段落

  Since we know the measures of all three sides of the retaining wall, we can use the Law of Cosines to find the measures of the angles formed by adjacent walls. We will refer to the angle formed by side 1 and side 2 as $\begin{array}{r}\mathrm{\angle }A\end{array}$ , the angle formed by side 2 and side 3 as $\begin{array}{r}\mathrm{\angle }B\end{array}$ , and the angle formed by side 1 and side 3 as $\begin{array}{r}\mathrm{\angle }C\end{array}$ . First, we will find $\begin{array}{r}\mathrm{\angle }A\end{array}$ .
  ::由于我们了解保留墙所有三个侧面的测量标准,我们可以使用《科辛斯定律》找到相邻墙壁所形成角度的测量标准。我们将把侧1和侧2所形成的角度称为“A”类,将侧2和侧3所形成的角度称为“B”类,将侧1和侧3所形成的角度称为“C”类。 首先,我们将找到“A”类。

  播放段落

  $$\begin{array}{rlrl}{22}^2& ={12}^2+{18}^2-2(12)(18)\cos A& & \text{Law of Cosines}\\ 484& =144+324-2(12)(18)\cos A& & \text{Simplify squares}\\ 484& =144+324-432\cos A& & \text{Multiply}\\ 484& =468-432\cos A& & \text{Add}\\ 16& =-432\cos A& & \text{Subtract}468\\ -0.037037037& \approx \cos A& & \text{Divide by}-432\\ {92.1}^{\circ }& \approx A& & {\cos }^{-1}(-0.037037037)\end{array}$$

  
  ::222=122+182-2(12)(18cos)Cosines484=144+324-2(12)(18cos)Acsociation squalis484=144+324 - 432cosAMultiply484=468 - 432cosAAdd16_432cosASubtract 688-0.0370037037cosAdivide by- 43292.1Acos-1(-0.37037037)

  播放段落

  Next we will find the measure of $\begin{array}{r}\mathrm{\angle }B\end{array}$ also by using the Law of Cosines.
  ::接下来,我们将通过使用《科辛定律》 来找到ZB的衡量标准。

  播放段落

  $$\begin{array}{rlrl}{18}^2& ={12}^2+{22}^2-2(12)(22)\cos B& & \text{Law of Cosines}\\ 324& =144+484-2(12)(22)\cos B& & \text{Simplify squares}\\ 324& =144+484-528\cos B& & \text{Multiply}\\ 324& =628-528\cos B& & \text{Add}\\ -304& =-528\cos B& & \text{Subtract}628\\ 0.575757576& =\cos B& & \text{Divide by}-528\\ {54.8}^{\circ }& \approx B& & {\cos }^{-1}(0.575757576)\end{array}$$

  
  ::182=122+2222-222-2(12)(22cos-BLLaw of Cosines 324=144+484-2(12)(22cos_BSimplicization sqos 324=144+484-528cosBmultiply 324=628-528cos_BAdd_304528cos_BSubtreme 6280.575757576=cosBDivide by-52854.8._Bcos-1 (0575757576)

  播放段落

  Now that we know two of the angles, we can find the third angle using the Triangle Sum Theorem, $\begin{array}{r}\mathrm{\angle }C=180-(92.1+54.8)={33.1}^{\circ }\end{array}$ .
  ::现在我们知道其中两个角度了, 我们可以找到第三个角度, 使用三角Sum Theorem, C=180-(92.1+54.8)=33.1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to figure out what the angle is of a triangle. 
  ::早些时候,有人要求你弄清楚三角形的角度是什么。

  播放段落

  You can use the Law of Cosines to solve this problem:
  ::您可以使用Casines定律解决这个问题:

  播放段落

  $$\begin{array}{r}{c}^2=a^2+b^2+2ab\cos \theta \\ {80}^2={50}^2+{50}^2+(2)(50)(50)\cos \theta \\ {80}^2-{50}^2-{50}^2=(2)(50)(50)\cos \theta \\ 6400-2500-2500=(2)(50)(50)\cos \theta \\ 1400=(2)(50)(50)\cos \theta \\ \cos \theta =\frac{1400}{5000}\\ \theta ={\cos }^{-1}(.28)\\ \theta ={73.74}^{\circ }\end{array}$$

  
  ::c2=a2+b2+2abcos=802=502+502+2(2)(50cos)=802-502-502=502=(2)(50cos)=6400-2500-2500=(2)(50cos=1400=(2)(50cos)=(2)(50cos)=14005000cos-1(28)=73。

  播放段落

  The angle in your paintball course is rather large, measuring $\begin{array}{r}{73.74}^{\circ }\end{array}$
  ::您的彩弹课角度相当大, 尺寸为73.74

  播放段落

  Example 2
  ::例2

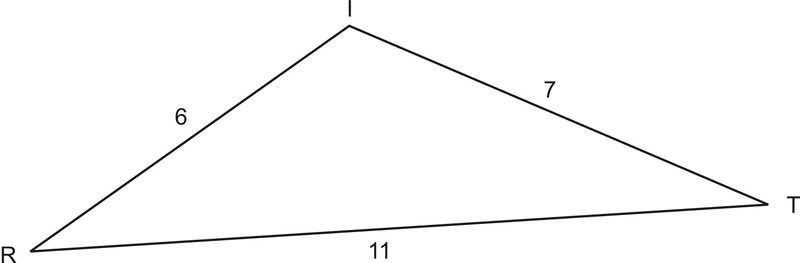
  播放段落

  Find the largest angle in the triangle below, where $\begin{array}{r}t=6,r=7,i=11\end{array}$
  ::查找下方三角形的最大角, t=6,r=7,i=11

  

  播放段落

  $\begin{array}{r}{11}^2=6^2+7^2-2\cdot 6\cdot 7\cdot \cos I,\mathrm{\angle }I\approx {115.4}^{\circ }\end{array}$
  ::112=62+72-267CosI,I115.4

  播放段落

  Example 3
  ::例3

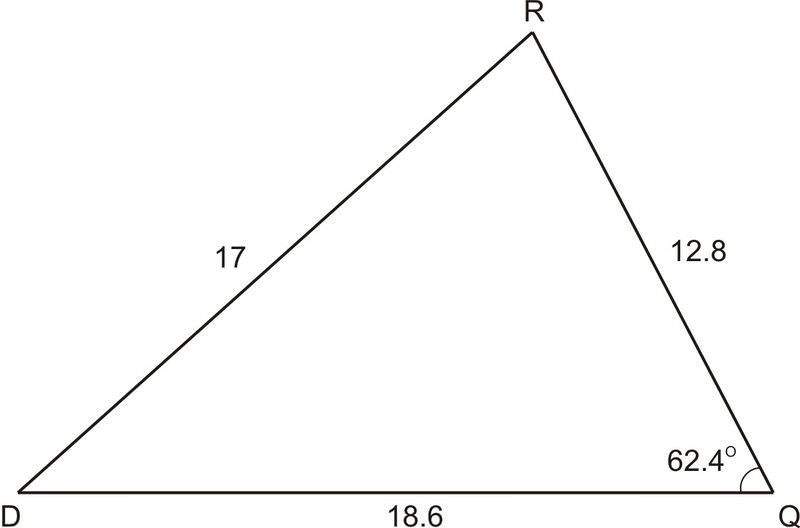
  播放段落

  Find the smallest angle in the triangle below, where $\begin{array}{r}q=17,d=12.8,r=18.6,\mathrm{\angle }Q={62.4}^{\circ }\end{array}$
  ::查找三角形下最小角, 其中q=17, d=12.8,r=18.6,62.4

  

  播放段落

  $\begin{array}{r}{12.8}^2={17}^2+{18.6}^2-2\cdot 17\cdot 18.6\cdot \cos D,\mathrm{\angle }D\approx {41.8}^{\circ }\end{array}$
  ::12.82 = 172+18.62-217_18_18_6_cosD,D41.8_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Example 4
  ::例4

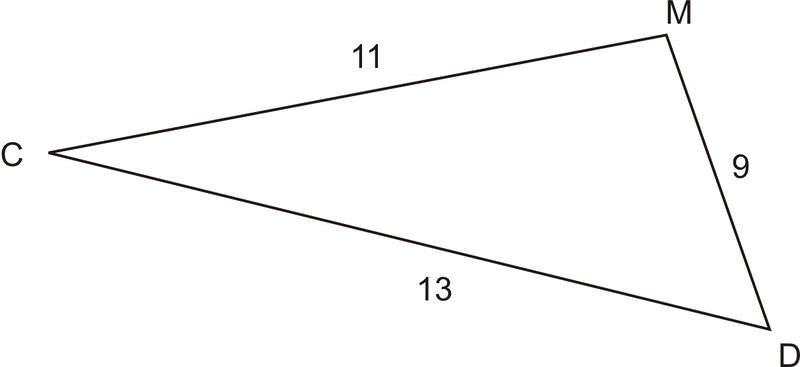
  播放段落

  Find the second largest angle in the triangle below, where $\begin{array}{r}c=9,d=11,m=13\end{array}$
  ::查找下方三角形中第二大角度, c=9, d=11, m=13

  

  播放段落

  $\begin{array}{r}{11}^2=9^2+{13}^3-2\cdot 9\cdot 13\cdot \cos D,\mathrm{\angle }D\approx {56.5}^{\circ }\end{array}$
  ::112=92+133-2913cD,D56.55

  播放段落

  Review
  ::回顾

  播放段落
  1. If you know the lengths of all three sides of a triangle, how can you identify the smallest angle of the triangle? The largest angle?
     ::如果您知道三角形所有三边的长度, 您如何识别三角形最小角度? 最大角度 ?
  播放段落
  2. If you know the measures of two angles of a triangle, how can you find the measure of the third angle?
     ::如果您知道三角形两个角度的度量, 您如何找到第三个角度的度量 ?

  播放段落

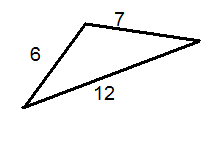
  Use the triangle below to answer questions 3-5.
  ::使用下面的三角形回答问题3-5。

  

  播放段落
  3. What is the measure of the smallest angle of the triangle?
     ::三角形最小角度的量度是多少?
  播放段落
  4. What is the measure of the largest angle of the triangle?
     ::三角形最大角的量度是多少?
  播放段落
  5. What is the measure of the third angle of the triangle?
     ::三角形第三个角度的度量是多少?

  播放段落

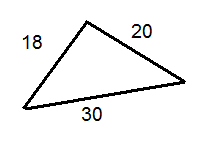
  Use the triangle below to answer questions 6-8.
  ::使用下面的三角形回答问题6-8。

  

  播放段落
  6. What is the measure of the smallest angle of the triangle?
     ::三角形最小角度的量度是多少?
  播放段落
  7. What is the measure of the largest angle of the triangle?
     ::三角形最大角的量度是多少?
  播放段落
  8. What is the measure of the third angle of the triangle?
     ::三角形第三个角度的度量是多少?

  播放段落

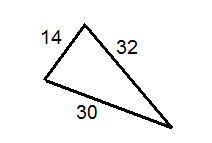
  Use the triangle below to answer questions 9-11.
  ::使用下面的三角形回答问题9-11。

  

  播放段落
  9. What is the measure of the smallest angle of the triangle?
     ::三角形最小角度的量度是多少?
  播放段落
  10. What is the measure of the largest angle of the triangle?
      ::三角形最大角的量度是多少?
  播放段落
  11. What is the measure of the third angle of the triangle?
      ::三角形第三个角度的度量是多少?

  播放段落

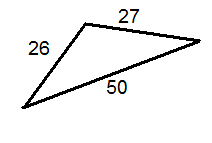
  Use the triangle below to answer questions 12-14.
  ::使用下面的三角形回答问题12-14。

  

  播放段落
  12. What is the measure of the smallest angle of the triangle?
      ::三角形最小角度的量度是多少?
  播放段落
  13. What is the measure of the largest angle of the triangle?
      ::三角形最大角的量度是多少?
  播放段落
  14. What is the measure of the third angle of the triangle?
      ::三角形第三个角度的度量是多少?

  播放段落

  Use the triangle below to answer questions 15-17.
  ::使用下面的三角形回答问题 15 -17。

  

  播放段落
  15. What is the measure of the smallest angle of the triangle?
      ::三角形最小角度的量度是多少?
  播放段落
  16. What is the measure of the largest angle of the triangle?
      ::三角形最大角的量度是多少?
  播放段落
  17. What is the measure of the third angle of the triangle?
      ::三角形第三个角度的度量是多少?

  播放段落

  Use the triangle below to answer questions 18-20.
  ::使用下面的三角形回答问题18-20。

  

  播放段落
  18. What is the measure of the smallest angle of the triangle?
      ::三角形最小角度的量度是多少?
  播放段落
  19. What is the measure of the largest angle of the triangle?
      ::三角形最大角的量度是多少?
  播放段落
  20. What is the measure of the third angle of the triangle?
      ::三角形第三个角度的度量是多少?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。