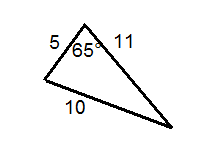5.3 确定三角的准确绘图

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 确定三角形的准确绘图

  Collapse Expand

  确定三角形的准确绘图

  播放段落

  Your friend is creating a new board game that involves several different triangle shaped pieces. However, the game requires accurate measurements of several different pieces that all have to fit together. She brings some of the pieces to you and asks if you can verify that her measurements of the pieces' side lengths and angles are correct.
  ::你的朋友正在创建一个新的棋盘游戏, 它涉及多个不同的三角形形状块。 但是, 游戏需要精确测量几个不同的形状块, 而这些形状必须齐装在一起 。 她把一些碎片带给您, 并询问您是否可以核实她对碎片侧边长度和角度的测量正确 。

  播放段落

  You take out the first piece. According to your friend, the piece has sides of length 4 in, 5 in and 7 in, and the angle between the side of the length 4 and the side of length 5 is $\begin{array}{r}{78}^{\circ }\end{array}$ . She's very confident in the lengths of the sides, but not quite sure if she measured the angle correctly. Is there a way to determine if your friend's game piece has the correct measurements, or did she make a mistake?
  ::你取出第一块。 据你朋友说, 第一块有4长的两边, 5长的和7长的两边, 4长的两边和5长的两边之间的角度是78。 她对两边的长度非常有信心, 但不确定她是否正确测量了角度。 是否有办法确定您朋友的游戏片的尺寸是否正确, 或者她犯了错误?

  播放段落

  Analyzing Triangles
  ::分析三角形

  播放段落

  Our extension of the analysis of triangles draws us naturally to oblique triangles.
  ::我们三角分析的延伸自然将我们引向斜三角。

  播放段落

  The can be used to verify that drawings of oblique triangles are accurate. In a right triangle, we might use the to verify that all three sides are the correct length, or we might use trigonometric ratios to verify an angle measurement. However, when dealing with an obtuse or acute triangle, we must rely on the Law of Cosines.
  ::它可以用来验证斜三角形的图纸是否准确。 在右三角形中,我们可以使用三角形来验证所有三边的长度是否正确,或者使用三角比来验证角度测量。 但是,在处理斜三角形或尖三角形时,我们必须依靠科斯尼定律。

  播放段落

  For the following problems, let's  use the Law of Cosines
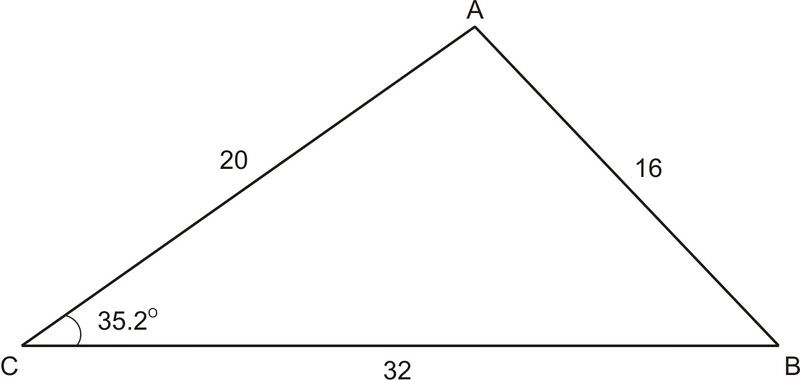
  ::对于以下的问题,让我们使用《科斯定律》

  播放段落

  1. In $\begin{array}{r}\mathrm{△}ABC\end{array}$ at the right, $\begin{array}{r}a=32,b=20\end{array}$ , And $\begin{array}{r}c=16\end{array}$ . Is the drawing accurate if it labels $\begin{array}{r}\mathrm{\angle }C\end{array}$ as $\begin{array}{r}{35.2}^{\circ }\end{array}$ ? If not, what should $\begin{array}{r}\mathrm{\angle }C\end{array}$ measure?
  ::1. 在“ABC”右边的“a=32,b=20”和“c=16”中,如果将“C”标为“35.2”是否准确?如果不是,“C”应测量什么?

  

  播放段落

  We will use the Law of Cosines to check whether or not $\begin{array}{r}\mathrm{\angle }C\end{array}$ is $\begin{array}{r}{35.2}^{\circ }\end{array}$ .
  ::我们将使用《科辛斯定律》来检查C是否为35.2。

  播放段落

  $$\begin{array}{rlrl}{16}^2& ={20}^2+{32}^2-2(20)(32)\cos 35.2& & \text{Law of Cosines}\\ 256& =400+1024-2(20)(32)\cos 35.2& & \text{Simply squares}\\ 256& =400+1024-1045.94547& & \text{Multiply}\\ 256& \ne 378.05453& & \text{Add and subtract}\end{array}$$

  
  ::162=202+322-2(20)(32cos=32cos)35.2科辛斯法2556=400+1024-2(20)(32cos=35.2平方Simply 256=400+1024-1045.94547Multiply256378.5453Add和减去

  播放段落

  Since $\begin{array}{r}256\ne 378.05453\end{array}$ , we know that $\begin{array}{r}\mathrm{\angle }C\end{array}$ is not $\begin{array}{r}{35.2}^{\circ }\end{array}$ . Using the Law of Cosines, we can figure out the correct measurement of $\begin{array}{r}\mathrm{\angle }C\end{array}$ .
  ::自256378.05453以来,我们知道C不是35.2。运用科辛定律,我们可以找出C的正确度量。

  播放段落

  $$\begin{array}{rlrl}{16}^2& ={20}^2+{32}^2-2(20)(32)\cos C& & \text{Law of Cosines}\\ 256& =400+1024-2(20)(32)\cos C& & \text{Simplify Squares}\\ 256& =400+1024-1280\cos C& & \text{Multiply}\\ 256& =1424-1280\cos C& & \text{Add}\\ -1168& =-1280\cos C& & \text{Subtract}1424\\ 0.9125& =\cos C& & \text{Divide}\\ {24.1}^{\circ }& \approx \mathrm{\angle }C& & {\cos }^{-1}(0.9125)\end{array}$$

  
  ::162=202+322-2(20)(32cos=CosinesClaw)256=400+1024-2(20)(32cos=Coslimize Squalis256=40000+1024-1280cos@CMultiply256=1424-1280cosCAdd-11681280cos*CSubtrol 14240.9125=CosCDivide24.1Ccos-1(0.9125)

  播放段落

  For some situations, it will be necessary to utilize not only the Law of Cosines, but also the Pythagorean Theorem and trigonometric ratios to verify that a triangle or quadrilateral has been drawn accurately.
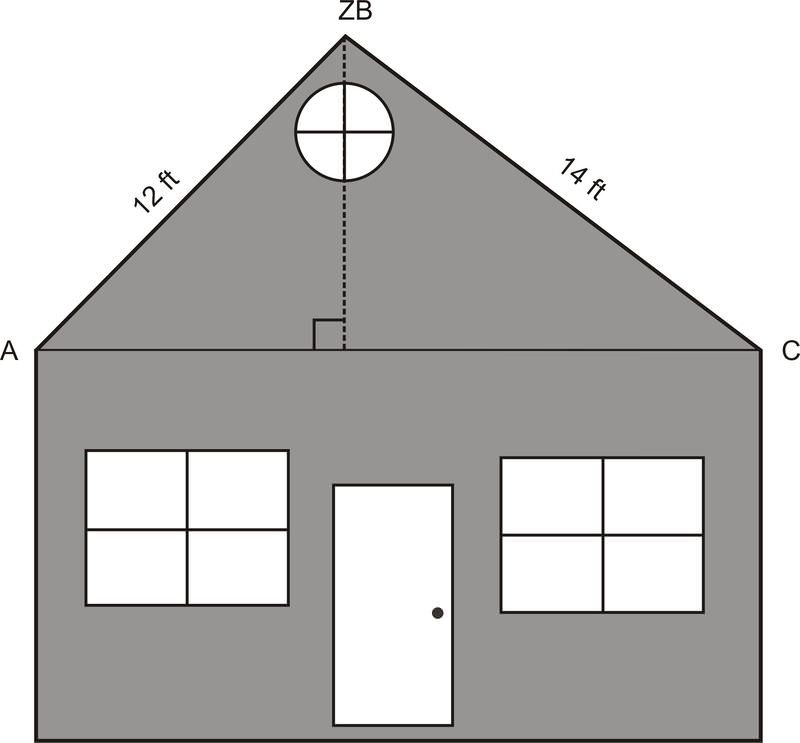
  ::对于某些情况,不仅需要利用科斯定律,还需要利用毕达哥里安理论和三角比,以核实三角或四边形是否准确绘制。

  播放段落

  2. A builder received plans for the construction of a second-story addition on a house. The diagram shows how the architect wants the roof framed, while the length of the house is 20 ft. The builder decides to add a perpendicular support beam from the peak of the roof to the base. He estimates that new beam should be 8.3 feet high, but he wants to double-check before he begins construction. Is the builder’s estimate of 8.3 feet for the new beam correct? If not, how far off is he?
  ::2. 建筑商收到在房屋上建造第二层楼的计划,图中显示建筑商如何希望盖住屋顶,而房屋的长度是20英尺。建筑商决定从屋顶的顶部到基地增加一个垂直的支撑光束,他估计新梁高8.3英尺,但他想在建筑开始之前再检查一次。建筑商对新梁的8.3英尺的估计是否正确?如果不正确,他距离多远?

  

  播放段落

  I f we knew either $\begin{array}{r}\mathrm{\angle }A\end{array}$ or $\begin{array}{r}\mathrm{\angle }C\end{array}$ , we could use trigonometric ratios to find the height of the support beam. However, neither of these angle measures are given to us. Since we know all three sides of $\begin{array}{r}\mathrm{△}ABC\end{array}$ , we can use the Law of Cosines to find one of these angles. We will find $\begin{array}{r}\mathrm{\angle }A\end{array}$ .
  ::如果我们知道“A”或“C”两个方面,我们可以使用三角比来找到支持光束的高度。然而,这些角度措施都没有提供给我们。既然我们知道“ABC”的所有三个方面,我们可以使用“Cosines”法来找到其中一个角度。我们会找到“A”。

  播放段落

  $$\begin{array}{rlrl}{14}^2& ={12}^2+{20}^2-2(12)(20)\cos A& & \text{Law of Cosines}\\ 196& =144+400-480\cos A& & \text{Simplify}\\ 196& =544-480\cos A& & \text{Add}\\ -348& =-480\cos A& & \text{Subtract}\\ 0.725& =\cos A& & \text{Divide}\\ {43.5}^{\circ }& \approx \mathrm{\angle }A& & {\cos }^{-1}(0.725)\end{array}$$

  
  ::142=122+202-2(12)(20cos)Cosines196=144+400-480-480cos ASimplify196=544-480cosAAdd-348}480cos*ASubtrol0.725=cosAdivide43.5Acos-1(0.725)

  播放段落

  Now that we know $\begin{array}{r}\mathrm{\angle }A\end{array}$ , we can use it to find the length of $\begin{array}{r}BD\end{array}$ .
  ::现在我们知道QA, 我们可以用它来找到BD的长度。

  播放段落

  $$\begin{array}{rl}\sin 43.5& =\frac{x}{12}\\ 12\sin 43.5& =x\\ 8.3& \approx x\end{array}$$

  
  ::=43.5=x1212sin =43.5=x8.3x

  播放段落

  Yes, the builder’s estimate of 8.3 feet for the support beam is accurate.
  ::是的,建筑商估计8.3英尺的支撑波束是准确的。

  播放段落

  In $\begin{array}{r}\mathrm{△}CIR,c=63,i=52\end{array}$ , and $\begin{array}{r}r=41.9\end{array}$ . Find the measure of all three angles.
  ::在 {CIR, c=63,i=52, r=41.9。 查找所有三个角度的度量 。

  播放段落

  $$\begin{array}{r}{63}^2={52}^2+{41.9}^2-2\cdot 52\cdot 41.9\cdot \cos C\\ {52}^2={63}^2+{41.9}^2-2\cdot 63\cdot 41.9\cdot \cos I\\ {180}^{\circ }-{83.5}^{\circ }-{55.1}^{\circ }={41.4}^{\circ }\\ \mathrm{\angle }C\approx {83.5}^{\circ }\\ \mathrm{\angle }I\approx {55.1}^{\circ }\\ \mathrm{\angle }R\approx {41.4}^{\circ }\end{array}$$

  
  ::632=522+41.92-25241.99C522=632+41.92-26341.99I18083.555.141.4C83.5I55.1R41.4

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked if there was a way to determine if your friend's game piece has the correct measurements. 
  ::之前有人问过你 有没有办法 确定你朋友的游戏片 是否有正确的量度

  播放段落

  Since your friend is certain of the lengths of the sides of the triangle, you should use those as the known quantities in the Law of Cosines and solve for the angle:
  ::既然你的朋友确定三角形两侧的长度, 您应该使用《科辛斯定律》中已知的数量, 并解决角度问题 :

  播放段落

  $$\begin{array}{r}{7}^2=5^2+4^2+(2)(5)(4)\cos \theta \\ 49=25+16+40\cos \theta \\ 49-25-16=40\cos \theta \\ \frac{8}{40}=\cos \theta \\ co{s}^{-1}\frac{8}{40}=\theta \\ \theta =78.46\end{array}$$

  
  ::72=52+42+(2)(5)(4)cos49=25+16+40cos49-25-16=40cos840=coscos-184078。

  播放段落

  So as it turns out, your friend is rather close. Her measurements were probably slight inaccurate because of her round off from the protractor.
  ::事实证明,你朋友很亲近 她的测量结果可能有点不准确

  播放段落

  Example 2
  ::例2

  播放段落

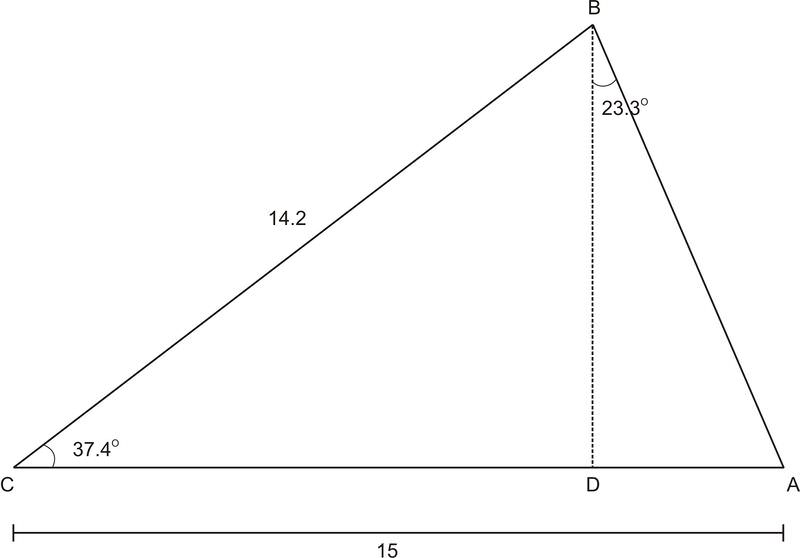
  Find $\begin{array}{r}AD\end{array}$ using the Pythagorean Theorem, Law of Cosines, trig functions, or any combination of the three.
  ::使用Pythagoren理论、Cosines定律、三角函数或三种函数的任何组合来查找AD。

  

  播放段落

  First, find $\begin{array}{r}AB\end{array}$ . $\begin{array}{r}A{B}^2={14.2}^2+{15}^2-2\cdot 14.2\cdot 15\cdot \cos {37.4}^{\circ },AB=\mathrm{9.4.}\sin {23.3}^{\circ }=\frac{AD}{9.4},AD=\mathrm{3.7.}\end{array}$
  ::首先,见AB.AB2=14.22+152-214.215cos37.4,AB=9.4.sin23.3AD9.4,AD=3.7。

  播放段落

  Example 3
  ::例3

  播放段落

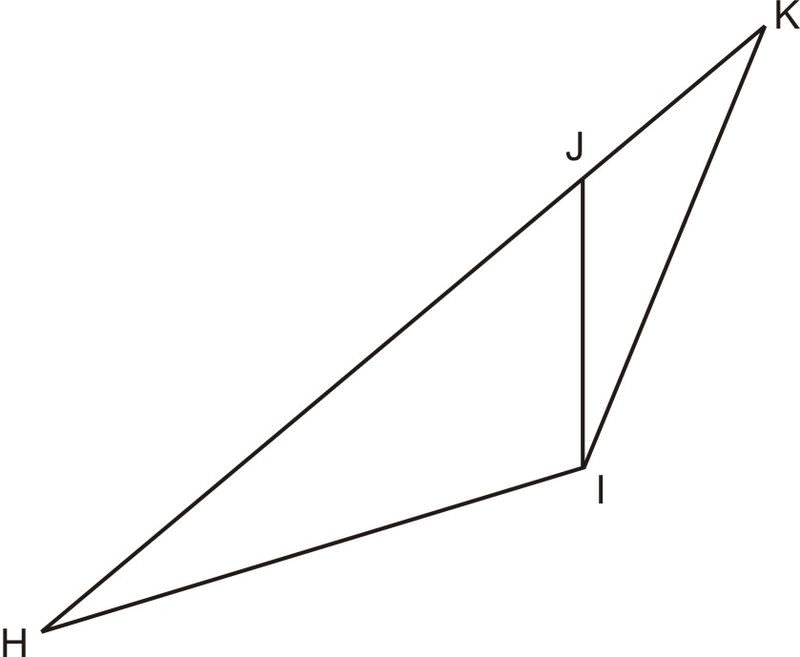
  Find $\begin{array}{r}HK\end{array}$ using the Pythagorean Theorem, Law of Cosines, trig functions, or any combination of the three if $\begin{array}{r}JK=3.6,KI=5.2,JI=1.9,HI=6.7\end{array}$ , and $\begin{array}{r}\mathrm{\angle }KJI={96.3}^{\circ }\end{array}$ .
  ::使用Pythagorean理论、Casines定律、三角函数或三种函数的任何组合查找香港,如果是JK=3.6、KI=5.2、JI=1.9、HI=6.7和ZQKJI=96.3。

  

  播放段落

  $\begin{array}{r}\mathrm{\angle }HJI={180}^{\circ }-{96.3}^{\circ }={83.7}^{\circ }\end{array}$ (these two angles are a linear pair). $\begin{array}{r}{6.7}^2=H{J}^2+{1.9}^2-2\cdot HJ\cdot 1.9\cdot \cos {83.7}^{\circ }\end{array}$ . This simplifies to the quadratic equation $\begin{array}{r}H{J}^2-0.417HJ-41.28\end{array}$ . Using the quadratic formula, we can determine that $\begin{array}{r}HJ\approx 6.64\end{array}$ . So, since $\begin{array}{r}HJ+JK=HK,6.64+3.6\approx HK\approx 10.24\end{array}$ .
  ::JJ=18096.383.7(这两个角度是线性对) 6.72=HJ2+1.92-2HJ1.9cos83.7。这简化了四边方程HJ2-0.417HJ-41.28。使用二次方程式,我们可以确定HJ6.64。因此,自HJ+JK=HK6.64+3.6HK10.24以来,我们可以确定HJ+JK=HK6.64+3.6HK。

  播放段落

  Example 4
  ::例4

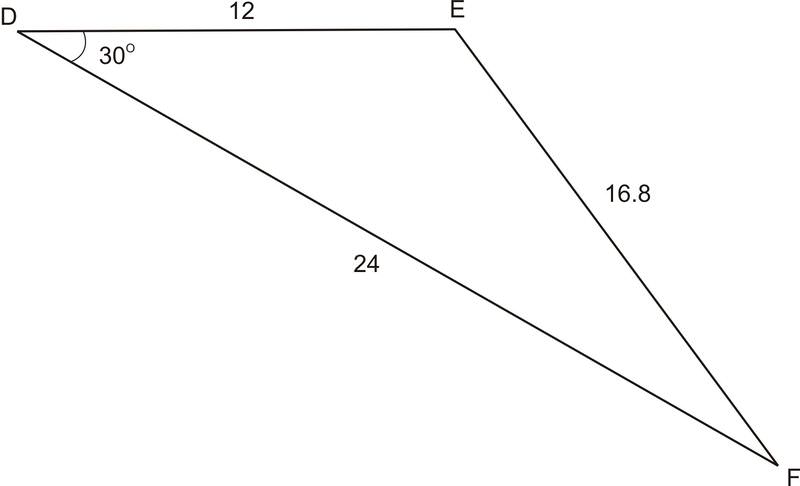
  播放段落

  Use the Law of Cosines to determine whether or not the following triangle is drawn accurately. If not, determine how far the measurement of side "d" is from the correct value.
  ::使用 Cosines 定律来确定以下三角形是否准确绘制。 如果没有, 请确定侧面“ d” 的测量距离正确值 。

  

  播放段落

  To determine this, use the Law of Cosines and solve for $\begin{array}{r}d\end{array}$ to determine if the picture is accurate. $\begin{array}{r}{d}^2={12}^2+{24}^2-2\cdot 12\cdot 24\cdot \cos {30}^{\circ },d=14.9\end{array}$ , which means $\begin{array}{r}d\end{array}$ in the picture is off by 1.9.
  ::要确定这一点,请使用《科辛定律》,并解决d,以确定图片是否准确。 d2=122+242-21224cos30d=14.9,这意味着图片中的d值为1.9。

  播放段落

  Review
  ::回顾

  播放段落
  1. If you know the lengths of all three sides of a triangle and the measure of one angle, how can you determine if the triangle is drawn accurately?
     ::如果您知道三角形所有三边的长度以及一个角度的度量, 您如何确定三角形是否准确绘制 ?

  播放段落

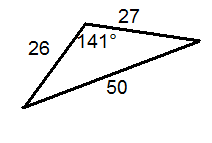
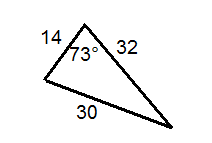
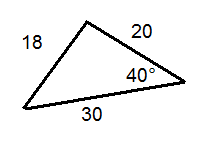
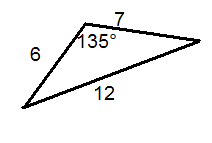
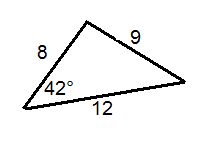
  Determine whether or not each triangle is labelled correctly.
  ::确定每个三角形的标签是否正确 。

  2. 
  3. 
  4. 
  5. 
  6. 
  7. 

  播放段落

  Determine whether or not each described triangle is possible. Assume angles have been rounded to the nearest degree.
  ::确定每个描述的三角形是否都可能。 假设角度已四舍五入到最接近的程度 。

  播放段落
  8. In $\begin{array}{r}\mathrm{△}BCD\end{array}$ , b=4, c=4, d=5, and $\begin{array}{r}m\mathrm{\angle }B={51}^{\circ }\end{array}$ .
     ::在“BCD”中, b=4, c=4, d=5, mB=51。
  播放段落
  9. In $\begin{array}{r}\mathrm{△}ABC\end{array}$ , a=7, b=4, c=9, and $\begin{array}{r}m\mathrm{\angle }B={34}^{\circ }\end{array}$ .
     ::在 ABC 中, a=7, b=4, c=9, mB=34, mB=34。
  播放段落
  10. In $\begin{array}{r}\mathrm{△}BCD\end{array}$ , b=3, c=2, d=7, and $\begin{array}{r}m\mathrm{\angle }D={138}^{\circ }\end{array}$ .
      ::在“BCD”中, b=3, c=2, d=7, mD=138。
  播放段落
  11. In $\begin{array}{r}\mathrm{△}ABC\end{array}$ , a=8, b=6, c=13.97, and $\begin{array}{r}m\mathrm{\angle }C={172}^{\circ }\end{array}$ .
      ::ABC中,a=8,b=6,c=13.97,和mC=172。
  播放段落
  12. In $\begin{array}{r}\mathrm{△}ABC\end{array}$ , a=4, b=4, c=9, and $\begin{array}{r}m\mathrm{\angle }B={170}^{\circ }\end{array}$ .
      ::在 ABC 中, a= 4, b=4, c=9, mB=170 。
  播放段落
  13. In $\begin{array}{r}\mathrm{△}BCD\end{array}$ , b=3, c=5, d=4, and $\begin{array}{r}m\mathrm{\angle }C={90}^{\circ }\end{array}$ .
      ::在“BCD”中, b=3, c=5, d=4, mC=90。
  播放段落
  14. In $\begin{array}{r}\mathrm{△}ABC\end{array}$ , a=8, b=3, c=6, and $\begin{array}{r}m\mathrm{\angle }A={122}^{\circ }\end{array}$ .
      ::在“ABC”中,a=8,b=3,c=6,m=A=122。
  播放段落
  15. If you use the Law of Cosines to solve for $\begin{array}{r}m\mathrm{\angle }C\end{array}$ in $\begin{array}{r}\mathrm{△}ABC\end{array}$ where a=3, b=7, and c=12, you will an error. Explain why.
      ::如果您使用 cosines 法则来解析在 QABC 中的 mC , 其中 a= 3, b=7, 和 c=12, 您将会出错 。 请解释原因 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。