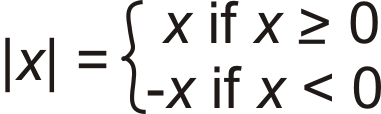Course: 1.13 解决绝对值 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 解决绝对值

Collapse Expand
解决绝对值
To determine the height of skeletal remains, archaeologists use the equation $\begin{align*}H=2.26f + 66.4\end{align*}$ , where H is the height in centimeters and f is the length of the skeleton's femur (also in cm). The equation has a margin of error of $\begin{align*} \pm 3.42 cm\end{align*}$ . Dr. Jordan found a skeletal femur that is 46.8 cm. Determine the greatest height and the least height of this person.
::为了确定骨骼遗骸的高度,考古学家使用H=2.26f+66.4的方程,其中H是厘米高度,f是骨骼股骨长度(也以厘米计)。方程误差幅度为+3.42厘米。约旦医生发现一个骨骼股骨为46.8厘米。确定此人的最大高度和最小高度。

Absolute Value Equations
::绝对绝对值

Absolute value is the distance a number is from zero. Because distance is always positive, the absolute value will always be positive. Absolute value is denoted with two vertical lines around a number, $\begin{align*}|x|\end{align*}$ .
::绝对值是数字从零的距离。因为距离总是正数, 绝对值总是正数。绝对值用数字周围的两条垂直线表示 :\\\\ x\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\。

$\begin{aligned} | 5 | = 5 & | - 9 | = 9 & | 0 | = 0 & | - 1 | = 1 \end{aligned}$
$\begin{align*}|5| = 5 && |-9| = 9 && |0| = 0 && |-1| = 1\end{align*}$

When solving an absolute value equation, the value of $\begin{align*}x\end{align*}$ could be two different possibilities; whatever makes the absolute value positive OR whatever makes it negative. Therefore , there will always be TWO answers for an absolute value equation.
::当解决绝对值方程式时,x的值可以是两种不同的可能性;无论绝对值是正数,还是负数。因此,绝对值方程式总是有两个答案。

If $\begin{align*}|x|=1\end{align*}$ , then $\begin{align*}x\end{align*}$ can be 1 or -1 because $\begin{align*}|1| = 1\end{align*}$ and $\begin{align*}|-1| = 1\end{align*}$ .
::如果\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

If $\begin{align*}|x|=15\end{align*}$ , then $\begin{align*}x\end{align*}$ can be 15 or -15 because $\begin{align*}|15| = 15\end{align*}$ and $\begin{align*}|-15| = 15\end{align*}$ .
::如果x*% 15, 那么x可以是 15 或 - 15, 因为% 15 15 和 + 15 15 。

From these statements we can conclude:
::从这些发言中,我们可以得出以下结论:

Let's determine if $\begin{align*}x = -12\end{align*}$ is a solution to $\begin{align*}|2x-5|=29\end{align*}$ .
::让我们确定 x12 是否是 2x-529 的解决方案。

Plug in -12 for $\begin{align*}x\end{align*}$ to see if it works.
::x 插插到 - 12 中以查看它是否有效。

$\begin{aligned} | 2 (- 12) - 5 | & = 29 \\ | - 24 - 5 | & = 29 \\ | - 29 | & = 29 \end{aligned}$
$\begin{align*}|2(-12)-5| &= 29\\ |-24-5| &= 29 \\ |-29| &= 29\end{align*}$

-12 is a solution to this absolute value equation.
::-12是这个绝对价值方程式的解决方案

Now, let's solve the following absolute value equations.
::现在,让我们解决以下的绝对值方程。

Solve $\begin{align*}|x+4|=11\end{align*}$ .
::解决 x+4 11 。

There are going to be two answers for this equation. $\begin{align*}x + 4\end{align*}$ can equal 11 or -11.
::此方程将有两个答案。 x+4 可等于 11 或 - 11 。

$\begin{aligned} | x + 4 | = 11 \\ ↙↘ \\ x + 4 = 11 x + 4 = - 11 \\ o r \\ x = 7 x = - 15 \end{aligned}$
$\begin{align*}& \qquad \quad |x+4|=11\\ & \qquad \quad \ \ \swarrow \searrow\\ & x+4 = 11 \quad x+4=-11\\ & \qquad \qquad \ \ or \qquad \qquad\\ & \quad \ \ x =7 \qquad \quad x=-15\end{align*}$
::x+411x+4=11x+411 或 x=7x15

Test the solutions:
::测试解决方案 :

$\begin{aligned} | 7 + 4 | = 11 | - 15 + 4 | = 11 \\ | 11 | = 11 | - 11 | = 11 \end{aligned}$
$\begin{align*}& |7+4|=11 \qquad |-15+4|=11 \\ & \quad \ |11|=11 \ \qquad \ |-11|=11 \end{align*}$

Solve $\begin{align*}\bigg | \frac{2}{3}x-5 \bigg |=17\end{align*}$ .
::解决23x517

Here, what is inside the absolute value can be equal to 17 or -17.
::在这里,绝对值之内的值可以等于17或17。

$\begin{aligned} | \frac{2}{3} x - 5 | = 17 \\ ↙↘ \\ \frac{2}{3} x - 5 = 17 \frac{2}{3} x - 5 = - 17 \\ \frac{2}{3} x = 22 o r \frac{2}{3} x = - 12 \\ x = 22 \cdot \frac{3}{2} x = - 12 \cdot \frac{3}{2} \\ x = 33 x = - 18 \end{aligned}$
$\begin{align*}& \qquad \quad \qquad \bigg | \frac{2}{3}x-5 \bigg |=17\\ & \qquad \qquad \quad \ \swarrow \searrow\\ & \frac{2}{3}x-5=17 \qquad \quad \frac{2}{3}x-5=-17\\ & \quad \ \ \frac{2}{3}x=22 \qquad or \quad \ \ \frac{2}{3}x=-12\\ & \qquad \ x=22 \cdot \frac{3}{2} \qquad \qquad x=-12 \cdot \frac{3}{2}\\ & \qquad \ x=33 \qquad \quad \quad \quad \ x=-18\end{align*}$
::23x517 23x5=1723x-5}17 23x=22or 23x*12 x=2232x*12*32 x=33x_18

Test the solutions:
::测试解决方案 :

$\begin{aligned} | \frac{2}{3} (33) - 5 | = 17 | \frac{2}{3} (- 18) - 5 | = 17 \\ | 22 - 5 | = 17 | - 12 - 5 | = 17 \\ | 17 | = 17 | - 17 | = 17 \end{aligned}$
$\begin{align*}& \bigg | \frac{2}{3}(33)-5 \bigg |=17 \qquad \quad \ \bigg | \frac{2}{3}(-18)-5\bigg |=17\\ & \quad \ \ |22-5|=17 \ \qquad \ \ |-12-5|=17\\ & \qquad \quad \ |17|=17 \qquad \qquad \qquad |-17|=17\end{align*}$

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine the greatest height and the least height of the skeletons.
::早些时候,有人要求你确定骨骼的最大高度和最小的高度

First, we need to find the height of the skeleton using the equation $\begin{align*}H=2.26f+66.4\end{align*}$ , where $\begin{align*}f=46.8\end{align*}$ .
::首先,我们需要用方程式H=2.26f+66.4 找到骨架的高度,F=46.8。

$\begin{aligned} H & = 2.26 (46.8) + 66.4 \\ H & = 172.168 c m \end{aligned}$
$\begin{align*}H&=2.26(46.8)+66.4 \\ H&=172.168 cm\end{align*}$
::H=2.26(46.8)+66.4H=172.168厘米

Now, let's use an absolute value equation to determine the margin of error, and thus the greatest and least heights.
::现在,让我们使用绝对值方程来确定误差幅度, 从而确定最大和最小的高度。

$\begin{aligned} | x - 172.168 | = 3.42 \\ ↙↘ \\ x - 172.168 = 3.42 x - 172.168 = - 3.42 \\ o r \\ x = 175.588 x = 168.748 \end{aligned}$
$\begin{align*}& \qquad \qquad \qquad \quad |x-172.168|=3.42\\ & \qquad \qquad \qquad \quad \swarrow \searrow\\ & x-172.168 = 3.42 \quad x-172.168=-3.42\\ & \qquad \qquad \qquad \qquad or \qquad \qquad\\ & \quad \ \ x =175.588 \qquad \quad x=168.748\end{align*}$
::___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

So the person could have been a maximum of 175.588 cm or a minimum of 168.748 cm. In inches, this would be 69.13 and 66.44 inches, respectively.
::因此,此人最多可达175.588厘米或最低168.748厘米。以英寸计,这分别为69.13和66.44英寸。

Example 2
::例2

Is $\begin{align*}x = -5\end{align*}$ a solution to $\begin{align*}|3x+22|=6\end{align*}$ ?
::x% 5 是解决 3x+22 6 的解决方案吗 ?

Plug in -5 for $\begin{align*}x\end{align*}$ to see if it works.
::x 插在 - 5 中, 检查它是否有效。

$\begin{aligned} | 3 (- 5) + 22 | = 6 \\ | - 15 + 22 | = 6 \\ | - 7 | \neq 6 \end{aligned}$
$\begin{align*}|3(-5)+22|=6\\ |-15+22|=6\\ |-7| \ne 6\end{align*}$

-5 is not a solution because $\begin{align*}|-7| = 7\end{align*}$ , not 6.
::-5不是解决之道,因为7+7,不是6

Example 3
::例3

Solve the following absolute value equation: $\begin{align*}|6x-11|+2=41\end{align*}$ .
::解决以下绝对值方程式:+6x-11+2=41。

Find the two solutions. Because there is a 2 being added to the left-side of the equation, we first need to subtract it from both sides so the absolute value is by itself.
::找到两个解决方案。因为方程左侧增加了一个 2, 因此我们首先需要从两侧减去它, 这样绝对值本身就足够了。

$\begin{aligned} | 6 x - 11 | + 2 = 41 \\ | 6 x - 11 | = 39 \\ ↙↘ \\ 6 x - 11 = 39 6 x - 11 = - 39 \\ 6 x = 50 6 x = - 28 \\ x = \frac{50}{6} o r x = - \frac{28}{6} \\ = \frac{25}{3} o r 8 \frac{1}{3} = - \frac{14}{3} o r - 4 \frac{2}{3} \end{aligned}$
$\begin{align*}& \qquad \ |6x-11|+2=41\\ & \qquad \qquad |6x-11|=39\\ & \qquad \quad \qquad \swarrow \searrow\\ & \ 6x-11=39 \quad 6x-11=-39\\ & \qquad \ 6x=50 \qquad \quad \ 6x=-28\\ & \qquad \quad x=\frac{50}{6} \quad or \quad \ \ x=-\frac{28}{6}\\ & \quad \qquad \ = \frac{25}{3} \ or \ 8 \frac{1}{3} \quad \ = - \frac{14}{3} \ or \ -4 \frac{2}{3}\end{align*}$
::6x-112=416x-11396x-11=366x-1139 6x=50 6x28x=506or x286=253或813143或-423

Check both solutions. It is easier to check solutions when they are improper fractions.
::检查两个解决方案。当解决方案是不当的分数时, 比较容易检查这些解决方案。

$\begin{aligned} | 6 (\frac{25}{3}) - 11 | & = 39 | 6 (- \frac{14}{3}) - 11 | = 39 \\ | 50 - 11 | & = 39 a n d | - 28 - 11 | = 39 \\ | 39 | & = 39 | - 39 | = 39 \end{aligned}$
$\begin{align*}\bigg |6 \left(\frac{25}{3}\right) -11 \bigg| & = 39 \qquad \qquad \quad \bigg |6 \left(- \frac{14}{3} \right) -11 \bigg| = 39\\ |50-11| &= 39 \ \quad and \qquad \ |-28-11| = 39 \\ |39| &= 39 \qquad \qquad \qquad \qquad \ \ |-39| = 39\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

Example 4
::例4

Solve the following absolute value equation: $\begin{align*}\bigg | \frac{1}{2}x+3 \bigg |=9\end{align*}$ .
::解析以下绝对值方程式 :\\ 12x+3\\ 9 。

What is inside the absolute value is equal to 9 or -9.
::绝对值内值等于9或9。

$\begin{aligned} | \frac{1}{2} x + 3 | = 9 \\ ↙↘ \\ \frac{1}{2} x + 3 = 9 \frac{1}{2} x + 3 = - 9 \\ \frac{1}{2} x = 6 o r \frac{1}{2} x = - 12 \\ x = 12 x = - 24 \end{aligned}$
$\begin{align*}& \qquad \bigg | \frac{1}{2}x+3\bigg |=9\\ & \qquad \quad \swarrow \searrow\\ & \frac{1}{2}x+3=9 \quad \frac{1}{2}x+3=-9\\ & \quad \ \ \frac{1}{2}x=6 \quad or \quad \frac{1}{2}x=-12\\ & \qquad \ x=12 \qquad \quad x=-24\end{align*}$
::12x+3912x+3=912x+3}9 12x=6or12x12 x=12x24

Test solutions:
::测试解决方案 :

$\begin{aligned} | \frac{1}{2} (12) + 3 | = 9 | \frac{1}{2} (- 24) + 3 | = 9 \\ | 6 + 3 | = 9 | - 12 + 3 | = 9 \\ | 9 | = 9 | - 9 | = 9 \end{aligned}$
$\begin{align*}& \bigg | \frac{1}{2} (12) +3 \bigg |=9 \qquad \quad \bigg | \frac{1}{2} (-24) +3 \bigg |=9\\ & \qquad |6+3|=9 \ \qquad \ \ |-12+3|=9 \\ & \qquad \quad \ \ |9|=9 \qquad \qquad \qquad \ \ |-9|=9\end{align*}$

Review
::回顾

Determine if the following numbers are solutions to the given absolute value equations.
::确定下列数字是否是给定绝对值方程的解决方案。

$\begin{align*}|x-7|=16;9\end{align*}$
::-716;9

$\begin{align*}|\frac{1}{4}x+1|=4;-8\end{align*}$
::14x+14;-8

$\begin{align*}|5x-2|=7;-1\end{align*}$
::5x-27;-1

Solve the following absolute value equations.
::解决以下绝对值方程式。

$\begin{align*}|x+3|=8\end{align*}$
::X+38

$\begin{align*}|2x|=9\end{align*}$
::2x% 9

$\begin{align*}|2x+15|=3\end{align*}$
::2x+153

$\begin{align*}\bigg |\frac{1}{3}x-5 \bigg |=2\end{align*}$
::13x-52

$\begin{align*}\bigg |\frac{x}{6}+4 \bigg |=5\end{align*}$
::X6+45

$\begin{align*}|7x-12|=23\end{align*}$
::7x-1223

$\begin{align*}\bigg |\frac{3}{5}x+2 \bigg |=11\end{align*}$
::35x+211

$\begin{align*}|4x -15|+1=18\end{align*}$
::4x -151=18

$\begin{align*}|-3x+20|=35\end{align*}$
::3x20+35

$\begin{align*}|12x-18|=0\end{align*}$
::12x-180

What happened in #13? Why do you think that is?
::13年发生什么了?

Challenge When would an absolute value equation have no solution? Give an example.
::绝对价值方程式何时无法解决问题?举个例子。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

解决绝对值

Absolute Value Equations ::绝对绝对值

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Absolute Value Equations
::绝对绝对值

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)