Course: 5.4 三角区公式的衍生

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 三角区公式的衍生

Collapse Expand
三角区公式的衍生
While in the lunch room with your friends one day, you're discussing different ways you can use the things you've learned in math class. You tell your friends that you've been learning a lot about triangles, such as how to find their area. One of your friends looks down at your plate and starts to smile.
::有一天,你和朋友在午餐室里讨论如何使用数学课学到的东西。你告诉朋友,你学到了很多三角形,比如如何找到它们的区域。你的一个朋友低头看你的盘子,开始微笑。

"Alright," he says. "If you're so good at things involving triangles, I dare you to find something simple. Tell me the area of your slice of pizza." He points down at the pizza on your plate.
::他说:“好吧,如果你对涉及三角形的事情很在行, 我敢让你找些简单的东西。告诉我,你那一块披萨的面积。”他指向你盘子上的披萨。

The pizza is shaped like a triangle. But unfortunately its not a right triangle. The outer edge is 5 inches long, and the long sides are 7 inches long. The angle between the edge and the long side of the slice is $\begin{align*}69^\circ\end{align*}$ . Is there any way to tell the area of your pizza slice?
::披萨形状像三角形。但不幸的是它不是右三角形。外缘5英寸长, 长边7英寸长。边缘与切片长边之间的角是69英寸。您的披萨切片面积有没有线索吗 ?

Deriving the Triangle Area Formula
::三角三角区公式

We can use the area formula from Geometry, $\begin{align*}A = \frac{1}{2} bh\end{align*}$ , as well as the sine function, to derive a new formula that can be used when the height, or altitude, of a triangle is unknown.
::我们可以使用来自几何的A=12bh的面积公式以及正弦函数来得出一个新的公式,当三角形的高度或高度未知时,就可以使用该公式。

In $\begin{align*}\triangle{ABC}\end{align*}$ below, $\begin{align*}BD\end{align*}$ is altitude from $\begin{align*}B\end{align*}$ to $\begin{align*}AC\end{align*}$ . We will refer to the length of $\begin{align*}BD\end{align*}$ as $\begin{align*}h\end{align*}$ since it also represents the height of the triangle. Also, we will refer to the area of the triangle as $\begin{align*}K\end{align*}$ to avoid confusing the area with $\begin{align*}\angle{A}\end{align*}$ .
::在以下的 ABC 中, BD 是 B 至 AC 的高度。我们将将 BD 的长度指为 h , 因为它也代表三角的高度。另外, 我们将将三角的面积指为 K , 以避免将区域与 QA 混淆。

$\begin{aligned} k & = \frac{1}{2} b h & Area of a triangle \\ k & = \frac{1}{2} b (c \sin A) & \sin A = \frac{h}{c} therefore c \sin A = h \\ k & = \frac{1}{2} b c \sin A & Simplify \end{aligned}$
$\begin{align*}k & = \frac{1}{2}bh && \text{Area of a triangle} \\ k & = \frac{1}{2}b (c \sin A) && \sin A = \frac{h}{c}\ \text{therefore}\ c \sin A = h \\ k & = \frac{1}{2}bc \sin A && \text{Simplify}\end{align*}$
::k=12bhreaa 三角形的 k= 12b( csin @A) sin @ A= hc 因此 csin @ A= hk= 12bcsin @ 简化

We can use a similar method to derive all three forms of the area formula, regardless of the angle:
::我们可以使用类似的方法来得出所有三种形式的区域公式,不管角度如何:

$\begin{aligned} K & = \frac{1}{2} b c \sin A \\ K & = \frac{1}{2} a c \sin B \\ K & = \frac{1}{2} a b \sin C \end{aligned}$
$\begin{align*}K & = \frac{1}{2}bc \sin A \\ K & = \frac{1}{2}ac \sin B \\ K & = \frac{1}{2}ab \sin C \end{align*}$
::K=12bcsinAK=12acsinBK=12absinC

The formula $\begin{align*}K = \frac{1}{2} \ bc \sin A \end{align*}$ requires us to know two sides and the included angle (SAS) in a triangle. Once we know these three things, we can easily calculate the area of an oblique triangle .
::公式 K= 12 bcsinA 要求我们了解三角形中的两面和包括角度( SAS) 。一旦我们了解这三样东西, 我们就可以很容易地计算斜三角形的面积。

Finding the Area of a Triangle
::查找三角区域

1. In $\begin{align*}\triangle{ABC}, \angle{C} = 62^\circ, b = 23.9\end{align*}$ , and $\begin{align*}a = 31.6\end{align*}$ . Find the area of the triangle.
::1. 在 @ABC, @C=62,b=23.9和a=31.6中,请查找三角形的区域。

Using our new formula, $\begin{align*}K = \frac{1}{2} \ ab \sin C \end{align*}$ , plug in what is known and solve for the area.
::使用我们的新公式, K=12 absinC, 插入已知内容并解决此区域。

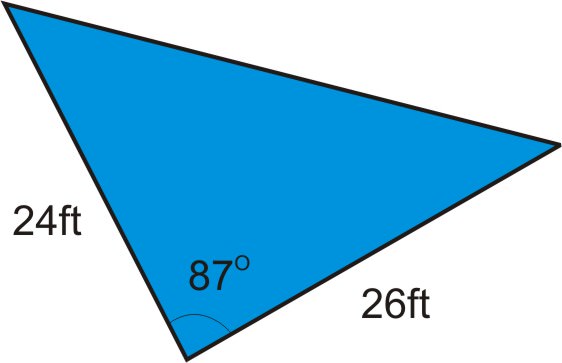
$\begin{aligned} K & = \frac{1}{2} (31.6) (23.9) \sin 62 \\ K & \approx 333.4 \end{aligned}$
$\begin{align*}K & = \frac{1}{2}(31.6)(23.9)\sin 62 \\ K & \approx 333.4\end{align*}$
::K=12(31.6)(23.9)sin62K333.4

2. The Pyramid Hotel recently installed a triangular pool. One side of the pool is 24 feet, another side is 26 feet, and the angle in between the two sides is $\begin{align*}87^\circ\end{align*}$ . If the hotel manager needs to order a cover for the pool, and the cost is $\begin{align*}\$ 35\end{align*}$ per square foot, how much can he expect to spend?
::2. 金字塔旅馆最近安装了一个三角游泳池:游泳池的一面是24英尺,另一面是26英尺,两侧之间的角是87英尺。如果旅馆经理需要订购游泳池的盖子,费用是每平方英尺35美元,他能花多少钱?

In order to find the cost of the cover, we first need to know the area of the cover. Once we know how many square feet the cover is, we can calculate the cost. In the illustration above, you can see that we know two of the sides and the included angle. This means we can use the formula $\begin{align*}K = \frac{1}{2} \ bc \sin A\end{align*}$ .
::为了找到覆盖的成本, 我们首先需要知道覆盖的面积。一旦我们知道覆盖的面积是多少平方英尺, 我们就可以计算成本。在上文的插图中, 您可以看到我们知道两个边和包含的角度。这意味着我们可以使用 K=12 bcsinA 公式。

$\begin{aligned} K = \frac{1}{2} (24) (26) \sin 87 \\ K \approx 311.6 \\ 311.6 s q . f t . \times $ 35 / s q . f t . = $ 10, 905.03 \end{aligned}$
$\begin{align*}& K = \frac{1}{2} \ (24)(26)\sin 87 \\ & K \approx 311.6 \\ & 311.6 \ sq. ft. \times \$ 35/sq. ft. = \$10,905.03 \end{align*}$
::K=12 (24)(26)(26)sin87K311.6311.6 sq.ft.x3美元/sq.ft.=10,905.03美元

The cost of the cover will be $\begin{align*}\$10,905.03\end{align*}$ .
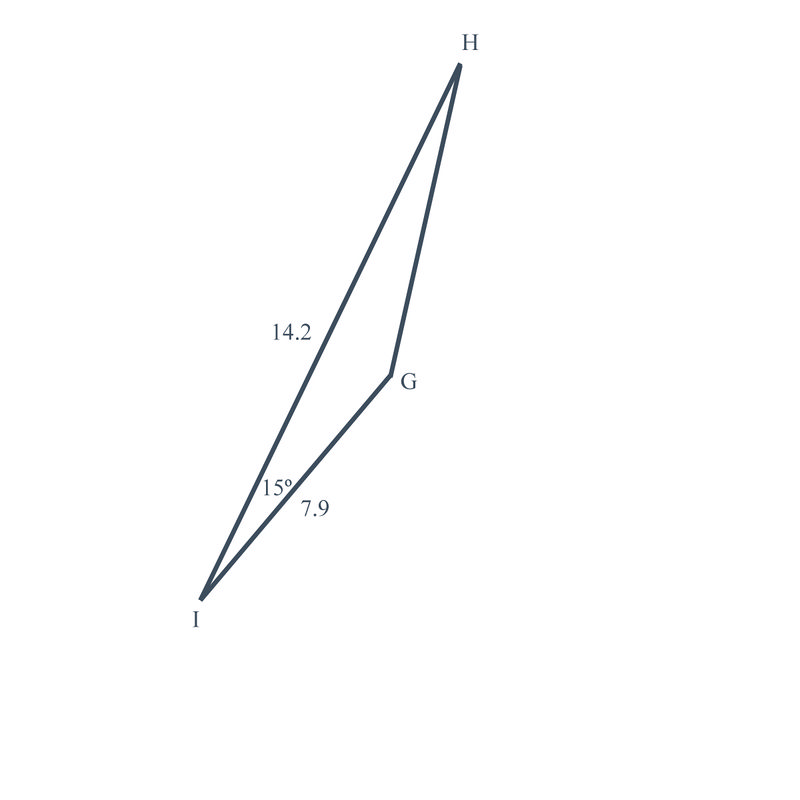
::费用为10 905.03美元。

3. In $\begin{align*}\triangle{GHI}, \angle{I} = 15^\circ, g = 14.2\end{align*}$ , and $\begin{align*}h = 7.9\end{align*}$ . Find the area of the triangle.
::3. 在 GHI, I=15g=14.2和h=7.9中, 找出三角形的面积。

Using our new formula, $\begin{align*}K = \frac{1}{2} \ ab \sin C \end{align*}$ , which is the same as $\begin{align*}K = \frac{1}{2} \ gh \sin I \end{align*}$ , plug in what is known and solve for the area.
::使用我们的新公式 K=12 absinC, 与 K=12 ghsinI 相同, 插入已知内容并解决此区域。

$\begin{aligned} K & = \frac{1}{2} (14.2) (7.9) \sin 15 \\ K & \approx 14.52 \end{aligned}$
$\begin{align*}K & = \frac{1}{2}(14.2)(7.9)\sin 15 \\ K & \approx 14.52\end{align*}$
::K=12(14.2)(7.9)sin15K14.52

Examples
::实例

Example 1
::例1

Earlier, you were asked if there was any way to tell the area of your pizza slice.
::之前有人问你有没有办法告诉你的披萨切片面积

Use the formula $\begin{align*}K = \frac{1}{2} \ bc \sin A\end{align*}$
::使用公式 K=12 bcsinA

where in this case, one of the sides is equal to 5, the other is equal to 7, and the angle is $\begin{align*}69^\circ\end{align*}$ .
::在这种情况下,一方等于5,另一方等于7,角度为69。

$\begin{align*}K = \frac{1}{2} (5)(7) \sin 69^\circ = 16.34 in^2\end{align*}$
::K=12(5)(7)(7)sin6916.34英寸2

Example 2
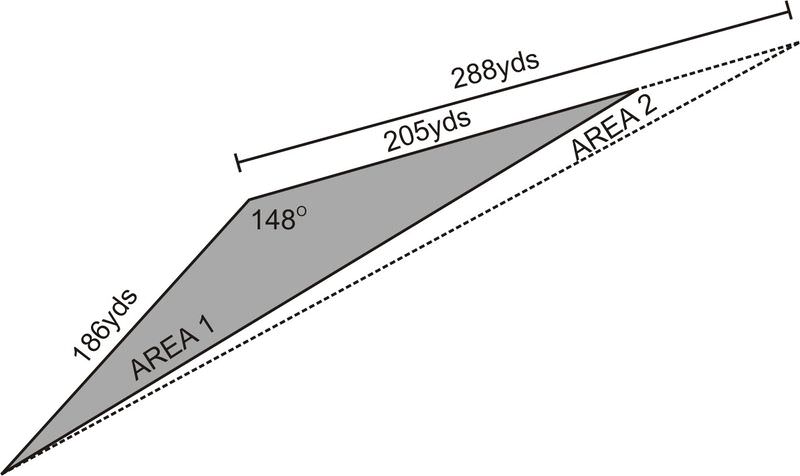
::例2

A farmer needs to replant a triangular section of crops that died unexpectedly. One side of the triangle measures 186 yards, another measures 205 yards, and the angle formed by these two sides is $\begin{align*}148^\circ\end{align*}$ .
::农民需要重新种植三边作物中意外死亡的部分。三角作物的一边是186码,另一边是205码,两边形成的角度是148。

What is the area of the section of crops that needs to be replanted?
::需要重新种植的那部分作物的面积是什么?

Use $\begin{align*}K = \frac{1}{2} \ bc \sin A, K= \frac{1}{2}(186)(205)\sin 148^\circ\end{align*}$ . So, the area that needs to be replaced is 10102.9 square yards.
::使用 K= 12 bcsinA, K= 12 (186)(205)sin148 。因此, 需要替换的区域是 10102.9 平方码。

Example 3
::例3

The farmer goes out a few days later to discover that more crops have died. The side that used to measure 205 yards now measures 288 yards. How much has the area that needs to be replanted increased by?
::农夫几天后出去发现更多的庄稼已经死亡。用来测量205码的那一面现在测量了288码。需要重新种植的面积增加了多少?

$\begin{align*}K = \frac{1}{2}(186)(288)\sin 148^\circ = 14193.4\end{align*}$ , the area has increased by 4090.5 yards.
::K=12(186)(288)sin14814193.4, 面积增加了4090.5码。

Example 4
::例4

Find the perimeter of the quadrilateral at the left If the area of $\begin{align*}\triangle{DEG} = 56.5\end{align*}$ and the area of $\begin{align*}\triangle{EGF} = 84.7\end{align*}$ .
::找到四边形在左侧的周界,如果是ZZDEG=56.5地区和QEGF=84.7地区。

You need to use the $\begin{align*}K = \frac{1}{2} \ bc \sin A\end{align*}$ formula to find $\begin{align*}DE\end{align*}$ and $\begin{align*}GF\end{align*}$ .
::您需要使用 K=12 bcsinA 公式查找 DE 和 GF 。

$\begin{aligned} 56.5 = \frac{1}{2} (13.6) D E \sin 39^{\circ} \to D E = 13.2 & 84.7 = \frac{1}{2} (13.6) E F \sin 60^{\circ} \to E F = 14.4 \end{aligned}$
$\begin{align*}56.5 = \frac{1}{2}(13.6)DE \sin 39^\circ \rightarrow DE = 13.2 && 84.7 = \frac{1}{2}(13.6)EF \sin 60^\circ \rightarrow EF = 14.4\end{align*}$
::56.5=12(13.6)DEsin39DE=132.84.7=12(13.6)EFsin60EF=14.4

Second, you need to find sides $\begin{align*}DG\end{align*}$ and $\begin{align*}GF\end{align*}$ using the .
::第二,你需要找到DG和GF的侧面,

$\begin{aligned} D G^{2} & = {13.2}^{2} + {13.6}^{2} - 2 \cdot 13.2 \cdot 13.6 \cdot \cos 39^{\circ} \to D G = 8.95 \\ G F^{2} & = {14.4}^{2} + {13.6}^{2} - 2 \cdot 14.4 \cdot 13.6 \cdot \cos 60^{\circ} \to G F = 14.0 \end{aligned}$
$\begin{align*}DG^2 & = 13.2^2 + 13.6^2 - 2 \cdot 13.2 \cdot 13.6 \cdot \cos 39^\circ \rightarrow DG = 8.95 \\ GF^2 & = 14.4^2 + 13.6^2 - 2 \cdot 14.4 \cdot 13.6 \cdot \cos 60^\circ \rightarrow GF = 14.0\end{align*}$
::DG2=13.22+13.62-213.213.6639DG=8.95GF2=14.42+13.62-22.4.413.6660GF=14.0。

The perimeter of the quadrilateral is 50.55.
::四边的周界是50.55

Review
::回顾

Find the area of each triangle.
::找到每个三角形的区域。

$\begin{align*}\triangle ABC\end{align*}$ if a=13, b=15, and $\begin{align*}m\angle C=71^\circ\end{align*}$ .
::a=13,b=15 和 mC=71。

$\begin{align*}\triangle ABC\end{align*}$ if b=8, c=4, and $\begin{align*}m\angle A=67^\circ\end{align*}$ .
::b=8,c=4,m=A=67。

$\begin{align*}\triangle ABC\end{align*}$ if b=34, c=29, and $\begin{align*}m\angle A=138^\circ\end{align*}$ .
::b=34,c=29,m=A=138。

$\begin{align*}\triangle ABC\end{align*}$ if a=3, b=7, and $\begin{align*}m\angle C=80^\circ\end{align*}$ .
::a=3,b=7,mC=80。

$\begin{align*}\triangle ABC\end{align*}$ if a=4.8, c=3.7, and $\begin{align*}m\angle B=43^\circ\end{align*}$ .
::a=4.8,c=3.7和mB=43。

$\begin{align*}\triangle ABC\end{align*}$ if a=12, b=5, and $\begin{align*}m\angle C=20^\circ\end{align*}$ .
::a=12, b=5, m=C=20, a=12, b=5, m=C=20, a=12, b=5, 和 m=C=20, a=12, b=5, 和 m=C=20, a=12, b=5

$\begin{align*}\triangle ABC\end{align*}$ if a=3, b=10, and $\begin{align*}m\angle C=50^\circ\end{align*}$ .
::a=3, b=10, mC=50。

$\begin{align*}\triangle ABC\end{align*}$ if a=5, b=9, and $\begin{align*}m\angle C=14^\circ\end{align*}$ .
::a=5,b=9,m*C=14,a=5,b=9。

$\begin{align*}\triangle ABC\end{align*}$ if a=5, b=7, and c=11.
::a=5,b=7,c=11,ABC=5,b=7,c=11。

$\begin{align*}\triangle ABC\end{align*}$ if a=7, b=8, and c=9.
::a=7,b=8,c=9的ABC。

$\begin{align*}\triangle ABC\end{align*}$ if a=12, b=14, and c=4.
::a=12,b=14,c=4,ABC=12,b=14,c=4。

A farmer measures the three sides of a triangular field and gets 114, 165, and 257 feet. What is the measure of the largest angle of the triangle?
::农民测量三角田的三面,获得114、165和257英尺。三角田的最大角是多少?

Using the information from the previous problem, what is the area of the field?
::利用上一个问题的信息,外地的领域是什么?

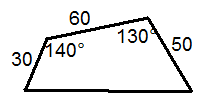
Another field is a quadrilateral where three sides measure 30, 50, and 60 yards, and two angles measure $\begin{align*}130^\circ\end{align*}$ and $\begin{align*}140^\circ\end{align*}$ , as shown below.
::另一个字段是四边形,三边测量30、50和60码,两个角度测量130和140,如下文所示。

Find the area of the quadrilateral. Hint: divide the quadrilateral into two triangles and find the area of each.
::查找四边形的区域。提示 : 将四边形分为两个三角形, 并找到每个三角形的区域。

Find the length of the fourth side.
::查找第四面的长度。

Find the measures of the other two angles.
::找出其他两个角度的度量。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

三角区公式的衍生

Deriving the Triangle Area Formula ::三角三角区公式

Finding the Area of a Triangle ::查找三角区域

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Deriving the Triangle Area Formula
::三角三角区公式

Finding the Area of a Triangle
::查找三角区域

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)